আজকে আমাদের আলোচনার বিষয়ঃ অনুপাত এবং সমানুপাত । এটি সপ্তম শ্রেনী গণিতের অনুপাত ও সমানুপাত এর অন্তর্গত।

অনুপাত এবং সমানুপাত
পূর্বের শ্রেণিতে আমরা কিন্তু অনুপাত সম্পর্কে ধারণা লাভ করে এসেছি, এবং দেখেছি, অনুপাত কীভাবে কাজ করে। এ অধ্যায়ে আমরা বিভিন্ন ধরণের অনুপাত সম্পর্কে জানার চেষ্টা করব। তার আগে চলো আমরা কয়েকটি কাজ করি।

তোমরা চিত্রের প্রাণিটিকে দেখোতো। তোমরা কি চিনতে পারছো প্রাণিটির নাম কি? এটি একটি জিরাফ। উচ্চতার দিক দিয়ে প্রাণিজগতের সবচেয়ে বড় প্রাণি জিরাফ। এবার জিরাফটি দেখো। এখানে, জিরাফটির গলার দৈর্ঘ্য ও জিরাফটির দৈর্ঘ্য মাপতে হবে। নির্দিষ্ট রেখা বরাবর তোমরা জিরাফটির গলা ও জিরাফটির দৈর্ঘ্য মাপো এবং গলা ও সম্পূর্ণ দৈর্ঘ্যের অনুপাতটি নির্ণয় করো।
আবার একইভাবে জিরাফটির দৈর্ঘ্য ও জিরাফটির গলার দৈর্ঘ্যের অনুপাত নির্ণয় করো। তুমি যে অনুপাত দুটি পেলে, সেটি নিচের ছকে লিখে ফেলো।

এবার তোমরা তোমাদের বাংলা বই ও গণিত বইটি নাও। দুটি বইয়েরই দৈর্ঘ্য, প্রস্থ ও পুরুত্ব মাপো। এবার গণিত বই ও বাংলা বইয়ের প্রাপ্ত দৈর্ঘ্যের অনুপাত নির্ণয় করো। একইভাবে প্রস্থ ও পুরুত্বের অনুপাতও নির্ণয় করো। এবার তোমার প্রাপ্ত তথ্যের সাপেক্ষে নিচের ছকটি পূরণ করো।
সরল অনুপাত:
এতক্ষণ আমরা তো বেশ কয়েকটি অনুপাত নির্ণয় করে এসেছি। তোমরা বলো তো এই অনুপাতগুলোতে কতটি রাশি ছিল? দেখো, প্রতিটি অনুপাতে কিন্তু ২ টি রাশি আছে। কোন অনুপাতে দুইটি রাশি থাকলে তাকে সরল অনুপাত বলে।
সরল অনুপাতের প্রথম রাশিকে পূর্ব রাশি এবং দ্বিতীয় রাশিকে উত্তর রাশি বলে। যেমন, ৩ : ৫ একটি সরল অনুপাত, এখানে ৩ হলো পূর্ব রাশি ও ৫ হলো উত্তর রাশি।

লঘু অনুপাত :
উপরে তোমরা জিরাফের দৈর্ঘ্য মেপে এসেছো। এখন, জিরাফের গলার দৈর্ঘ্য ও পুরো দেহের অনুপাতটি কি ছিল দেখো তো? অনুপাতের পূর্ব রাশি ও উত্তর রাশি মধ্যে কে বড় বলো তো? দেখতে যাবে পূর্ব রাশিটি ছোট উত্তর রাশিটি বড়। এধরণের অনুপাত গুলোকে লঘু অনুপাত বলা হয়। অর্থাৎ, সরল অনুপাতের পূর্ব রাশি, উত্তর রাশি থেকে ছোট হলে, তাকে লঘু অনুপাত বলে। যেমন, ৩ : ৫, ৪ : ৭ ইত্যাদি।
একটি বিদ্যালযের ৩য় শ্রেণির শিক্ষার্থীদের গড় বয়স ৮ বছর এবং ৫ম শ্রেণির শিক্ষার্থীদের গড় বয়স ১০ বছর। এখানে ৩য় ও ৫ম শ্রেণির শিক্ষার্থীদের গড় বয়সের অনুপাত ৮:১০ বা ৪ : ৫। এই অনুপাতটির পূর্ব রাশি, উত্তর রাশি অপেক্ষা ছোট হওয়ায় ইহা একটি লঘু অনুপাত।
গুরু অনুপাত :
আবার আমরা সেই জিরাফের দৈর্ঘ্যটির দিকে তাকাই। তবে এবার পুরো দেহের দৈর্ঘ্য ও গলার দৈর্ঘ্যের অনুপাত থেকে আমরা কি দেখতে পারি? এবার কিন্তু পূর্ব রাশিটি বড় এবং উত্তর রাশিটি ছোট। এধরণের অনুপাত হল গুরু অনুপাত ।
অর্থাৎ, কোনো সরল অনুপাতের পূর্ব রাশি, উত্তর রাশি থেকে বড় হলে, তাকে গুরু অনুপাত বলে। যেমন, ৫ :
৩, ৭ : ৪, ৬ : ৫ ইত্যাদি।
সাদিয়া ৩২ টাকা দিয়ে একটি বিস্কুটের প্যাকেট ও ২৫ টাকা দিয়ে একটি কোণ আইসক্রিম কিনলো ।
এখানে বিস্কুট ও আইসক্রিমের দামের অনুপাত হলো ৩২ : ২৫, এই অনুপাতটির পূর্ব রাশি ৩২ যা উত্তর রাশি ২৫ অপেক্ষা বড় হওয়ায় ইহা একটি গুরু অনুপাত।
একক অনুপাত:
তোমরা তোমাদের দুটো বইয়ের অনুপাত মেপে দেখেছো। সেখান থেকে কি পেলে বলো তো? দেখো তো দৈর্ঘ্যের অনুপাত কেমন হয়? দুটো বইয়ের দৈর্ঘ্যের অনুপাত একই বা কাছাকাছি না? অনুপাতের ধারণা থেকে আমরা কি বলতে পারি? দুটো বইয়ের দৈর্ঘ্য একই হওয়ায় আমরা এটিকে বলতে পারি ১:১। অর্থাৎ অনুপাতের দুটো রাশিই এক বা একক। এবং এধরণের অনুপাতই হল একক অনুপাত।
অর্থাৎ, যে সরল অনুপাতের পূর্ব রাশি ও উত্তর রাশি সমান সে অনুপাতকে একক অনুপাত বলে। যেমন, আরিফ ১৫ টাকা দিয়ে একটি বলপেন ও ১৫ টাকা দিয়ে একটি খাতা কিনলো। এখানে বলপেন ও খাতা উভয়টির মূল্য সমান এবং মূল্যের অনুপাত ১৫ : ১৫ বা ১:১। অতএব, একক অনুপাত ।
ব্যস্ত অনুপাত :
চলো, আমরা আবার সেই জিরাফটির কথা দেখি। তোমরা নিচের ছকে অনুপাত দুটির মধ্যে সম্পর্ক করার চেষ্টা করো তো।

ছক থেকে আসলে কি দেখতে পাচ্ছো? ১ নং অনুপাতের পূর্ব রাশিটি আর ২ নং অনুপাতের উত্তর রাশির মাঝে কোন মিল পাও? আবার ১ নং অনুপাতের উত্তর রাশি আর ২ নং অনুপাতের পূর্ব রাশির মাঝে কোন মিল পাও?
দেখো, এই দুটি অনুপাতের একটি আরেকটির সাপেক্ষে উলটো।
কোন সরল অনুপাতের পূর্ব রাশিকে উত্তর রাশি এবং উত্তর রাশিকে পূর্ব রাশি করে প্রাপ্ত অনুপাতকে পূর্বের অনুপাতের ব্যস্ত অনুপাত বলে।
যেমন, ১৩ : ৫ এর ব্যস্ত অনুপাত ৫: ১৩।
বহুরাশিক অনুপাত:
ভেবে দেখো, তুমি উপরে যে বই মাপলে, এবার তোমাকে বইগুলোর দৈর্ঘ্যের অনুপাত নির্ণয় করতে বললে তুমি কি করবে? এবার কি আগের মত কোন একক অনুপাত পাবে? তা কিন্তু পাবে না, কারণ এবার তোমার কিন্তু রাশি আর দুটি নিই। তাহলে এবার তোমাকে তিনটি রাশিকে পাশাপাশি অনুপাত আকারে লিখতে হবে। অর্থাৎ, তিন বা ততোধিক রাশির অনুপাতকে বহুরাশিক অনুপাত বলে।
এক্ষেত্রে পুর্বে ব্যবহার করে আসা একটি উদাহরণের সাহায্যে চিন্তা করো, আরিফ ১৫ টাকা দিয়ে একটি খাতা ও ১৫ টাকা দিয়ে একটি বলপেনের সাথে সাথে ১৫ টাকা দিয়ে একটি রাবারও কিনলো। এবার তাহলে মূল্যের অনুপাত কি হবে? নিশ্চয় ১৫ : ১৫ বা ১:১ হবে না। এক্ষেত্রে মূল্যের অনুপাত হবে ১৫ : ১৫ : ১৫ বা ১ : ১ : ১। এবার ভাবো উপরের উদাহরণ অনুযায়ী যদি সাদিয়া ৩২ টাকা দিয়ে বিস্কুটের প্যাকেট ও ২৫ টাকা দিয়ে কোণ আইসক্রিমের সাথে ২ টাকা দিয়ে একটি ক্যান্ডি কিনত, তাহলে এই তিনটি পণ্যের মূল্যের অনুপাত কত হত?
ধারাবাহিক অনুপাত :
উপরের ছকে ১ম অনুপাতের উত্তর রাশি ও দ্বিতীয় অনুপাতের পূর্ব রাশিটি কত দেখো তো? দুটি কি সমান হচ্ছে না?
এভাবে, দুটি অনুপাতের মধ্যে প্রথম অনুপাতের উত্তর রাশি ও দ্বিতীয় অনুপাতের পূর্ব রাশি পরস্পর সমান হলে, তাকে ধারাবাহিক অনুপাত বলে।
আবার চিন্তা করে দেখো, ধরো তুমি বাজারে গেলে। গিয়ে তুমি ১০ টাকা দিয়ে একটি চকলেট, ২০ টাকা দিয়ে একটি কেক এবং ৩০ টাকা দিয়ে একটি আইসক্রিম কিনলে। এখানে কি হচ্ছে ভাবো তো?
তোমার কেনা চকলেট ও কেকের দামের অনুপাতটি হবে ১০:২০ অথবা ১:২। আবার তোমার কেক এবং আইসক্রিমের দামের অনুপাতটি হবে ২০:৩০ বা ২:৩। এখানে কি আমরা আমাদের বলা উদাহরণের মত ঘটনা পাচ্ছি? দেখো, এই তিনটি অনুপাত কিন্তু ধারাবাহিক অনুপাতে আছে। অর্থাৎ, তোমরা কেনা চকলেট, কেক এবং আইসক্রিমের দামের অনুপাতটি হবে ১:২:৩।
বাস্তব সমস্যা সমাধানে অনুপাতের প্রয়োগ
১. ৫০০ টাকা দুইজন বন্ধুর মাঝে ২:৩ অনুপাতে ভাগ করে দিলে কে কত টাকা পাবে?
|
১ম বন্ধু |
১ম বন্ধু |
২য় বন্ধু |
২য় বন্ধু |
২য় বন্ধু |
অনুপাতের পূর্বরাশি ২ এবং উত্তর রাশি ৩। রাশি দুইটির সমষ্টি- ২+৩=৫।
১ম বন্ধু পাবে, ৫০০ টাকার ২/৫ অংশ=৫০০ টাকা× ২/৫=২০০ টাকা
২য় বন্ধু পাবে, ৫০০ টাকার = ৩/৫ অংশ=৫০০ টাকা × ৩/৫=৩০০ টাকা
অনুপাতের পূর্ব রাশি ও উত্তর রাশির সমষ্টি দ্বারা তাদেরকে ভাগ করে প্রত্যেকের অংশ নির্ণয় করা যায়।
২. দুইটি সংখ্যার যোগফল ৩৬০। সংখ্যা দুইটির অনুপাত ৪: ৫ হলে, সংখ্যা দুইটি নির্ণয় করো।
সংখ্যা দুইটির অনুপাত ৪: ৫
অনুপাতটির পূর্ব ও উত্তর রাশির যা যোগফল = 8 + ৫ = ৯।
প্রথম সংখ্যাটি = ৩৬০ এর ৪/৯ অংশ
= ৩৬০ × ৪/৯
=১৬০।
দ্বিতীয় সংখ্যাটি = ৩৬০ এর ৫/৯ অংশ
= ৩৬০ × ৫/৯=২০০।
নির্ণেয় সংখ্যা দুইটি হলো ১৬০ ও ২০০।
৩. কোন এক সোমবারে, তোমাদের নিকটস্থ বাজারে কেজিপ্রতি আলু ও বেগুনের দামের অনুপাত ৪:৯। আলুর দাম ২০ টাকা হলে বেগুনের দাম কত?
মঙ্গলবারে, বাজারে প্রাপ্যতার ঘাটতির জন্য বেগুনের দাম কেজিপ্রতি ৫ টা বৃদ্ধি পেলে নতুন অনুপাত কত হবে?
|
আলু |
আলু | আলু | আলু | বেগুন | বেগুন | বেগুন | বেগুন | বেগুন | বেগুন | বেগুন | বেগুন | বেগুন |
অনুপাতের পূর্বরাশি ৪ এবং উত্তর রাশি ৯। রাশি দুইটির সমষ্টি- ৪+৯=১৩।
আলুর দাম ২০ টাকা। এখানে, আলুর দাম মোট দামের ৪/১৩ অংশ। ও বেগুনের দাম মোট দামের ৯/১৩ অংশ।
আবার, মোট দাম ও আলুর দামের অনুপাত হবে তাহলে ১৩:৪।
তাহলে মোট দাম হবে আলুর দামের ১৩/৪ অংশ। অতএব মোট দাম হবে ২০ টাকা × ১৩/৪ = = ৬৫ টাকা
অতএব বেগুনের দাম হবে, ৬৫ টাকার ৯/১৩ অংশ = ৬৫ টাকা × ৯/১৩ = ৪৫ টাকা।
২. ৩০টি কমলা তিন ভাই স্বপন, তপন ও মননের মধ্যে ৫ : 3 : ২ অনুপাতে ভাগ করলে প্রত্যেকের কতটি করে কমলা পাবে কত ?
| স্বপন | স্বপন | স্বপন | স্বপন | স্বপন | তপন | তপন | তপন | মনন | মনন |
কমলার পরিমাণ = ৩০ টি
প্রদত্ত অনুপাত = ৫ : ৩ : ২। অনুপাতের সংখ্যাগুলোর যোগফল = ৫ + ৩ + ২ = ১০
স্বপন পায় = ৩০ টি কমলার ৫/১০ অংশ = ৩০ × ৫/১০ = ১৫ টি
তপন পায় = ৩০টি কমলার ৩/১০ অংশ = ৩০ × ৩/১০ = ৯ টি
মনন পায় = ৩০ টি কমলার ২/১০ অংশ = ৩০ × ২/১০ = ৬ টি
স্বপন, তপন ও মননের প্রাপ্ত কমলার পরিমাণ যথাক্রমে ১৫টি, ৯টি ও ৬টি।
অনুপাত সম্পর্কিত নিচের বাস্তব সমস্যাগুলি সমাধান করো :


মিশ্র অনুপাত
তোমরা দেখেছো দুটি বস্তুর দৈর্ঘ্য, প্রস্থ বা উচ্চতার ক্ষেত্রে তুলনা করতে অনুপাত ব্যবহার করা হয়। এখন নিচের জমি দুইটির মধ্যে তুলনা করার চেষ্টা করো।

দেখা যাচ্ছে যে, জমি দুইটির দৈর্ঘ্য একই। কিন্তু তাদের প্রস্থের অনুপাত = ১.৫/১ = ১.৫ঃ১ ।
আবার, জমির ক্ষেত্রফলের অনুপাতও কিন্তু ১.৫ × ১ /১ × ১ = ১.৫/১ = ১.৫ঃ১ ।
এ থেকে মনে হতে পারে প্রস্থের অনুপাত দিয়েই ক্ষেত্রফলের অনুপাত বের করা যায়।
কিন্তু আসলে কি তাই?
এবার তুমি নিচের বর্গ আকৃতির জমি দুইটির মধ্যে তুলনা করার চেষ্টা করে দেখ।
তোমার জানা দরকার একটি অপরটির তুলনায় কতগুণ বড় বা ছোট।
জমি দুইটির দৈর্ঘ্যের অনুপাত = ২/১ = ২ : ১। যদি আমরা এই অনুপাতের কথা চিন্তা করি তাহলে মনে হতে পারে যে, ২য় বর্গক্ষেত্রটি প্রথম বর্গক্ষেত্রের ২ গুণ। নিচের ছবি দেখে বলতো আসলেই এমন ভাবা ঠিক কিনা?

এখানে, দৈর্ঘ্য ও প্রস্থ উভয়েই ভিন্ন। তাই এক্ষেত্রে দৈর্ঘ্য ও প্রস্থ উভয়ের অনুপাত নিয়ে গুণ করলে তুলনাটা ঠিকঠাক হবে।
এখানে, জমির দৈর্ঘ্যের অনুপাত = ২/১ = ২ : ১ এবং জমির প্রস্থের অনুপাত = ২/১ = ২ : ১
অনুপার যেহেতু একটি ভগ্নাংশ তাই দুটি অনুপাত গুণ করলে পাওয়া যাবে = ২/১ × ১/২ = ২×২/১×১ = ৪/১ = ৪ : ১
তাহলে দেখা যাচ্ছে, শুধু দৈর্ঘ্য বা শুধু প্রস্থ দিয়ে তুলনা করলে কিন্তু চলবে না।
দৈর্ঘ্য ও প্রস্থ উভয়ের অনুপাত নিয়ে গুণ করলে জমির আকারের সঠিক অনুপাত পাওয়া যাবে।
আচ্ছা, সরাসরি ক্ষেত্রফল নির্ণয় করে তারপর অনুপাত নির্ণয় করলেই তো হয়। তাহলে আলাদা করে দৈর্ঘ্য ও প্রস্থের অনুপাত তো আর প্রয়োজন হয় না। ব্যাপারটা হলো উপরের উদাহরণগুলোতে দৈর্ঘ্য ও প্রস্থের মান সরাসরি দেওয়া আছে। কাজেই আলাদা করে ক্ষেত্রফল নির্ণয় করা সম্ভব। যদি শুধুমাত্র দুটি আয়তক্ষেত্রের দৈর্ঘ্য ও প্রস্থের অনুপাত দেওয়া হত তাহলে কিন্তু ক্ষেত্রফল নির্ণয় করা সম্ভব হতো না। তখন অনুপাতের ধারণা কাজে লাগিয়ে সহজেই তুমি তুলনা করতে পারবে? নিচের সমস্যাটি তেমনই একটি সমস্যা। তোমরা যা শিখলে সেটা কাজে লাগিয়ে সমাধান করো :
দুইটি আয়তাকার মাঠের দৈর্ঘ্যের অনুপাত ৪ঃ৩ এবং প্রস্থের অনুপাত ৬ঃ১। মাঠের ক্ষেত্রফলের অনুপাত কত হবে?
এভাবে, একাধিক সরল অনুপাতের পূর্ব রাশিগুলোর গুণফলকে পূর্ব রাশি এবং উত্তর রাশিগুলোর গুণফলকে উত্তর রাশি ধরে প্রাপ্ত অনুপাতকে মিশ্র অনুপাত বলে।
যেমন, ২:৩ এবং ৫:৭ সরল অনুপাতগুলোর মিশ্র অনুপাত হলো=(২×৫):(৩×৭)=১০:২১
উদাহরণঃ
প্রদত্ত সরল অনুপাতগুলোর মিশ্র অনুপাত নির্ণয় কর : ৫:৭, ৪:৯, ৩ : ২
সমাধান :
অনুপাত তিনটির পূর্ব রাশিগুলোর গুণফল ৫ × ৪ × ৩ = ৬০
এবং উত্তর রাশিগুলোর গুণফল = ৭ × ৯ × ২ = ১২৬
নির্ণেয় মিশ্র অনুপাত = ৬০ : ১২৬ বা ১০ : ২১
১) ২ : ৩ ও ৩ : ৪ অনুপাতদ্বয়ের মিশ্র অনুপাত নির্ণয় করো।
২) নিচের সরল অনুপাতগুলোকে মিশ্র অনুপাতে প্রকাশ কর :
(ক) ৩ : ৫, ৫ : ৭ ও ৭:৯ (খ) ৫:৩, ৭ : ৫ ও ৯ : ৭
৩) ত্রিমাত্রিক বস্তুর ক্ষেত্রে তুলনা করার সময় দৈর্ঘ্য, প্রস্থ ও উচ্চতা তিনটিই বিবেচনা করতে হয়।
অর্থাৎ, আয়তনের মাধ্যমে ত্রিমাত্রিক বস্তুর তুলনা সুবিধাজনক হয়।
এবার ভেবে দেখতো আয়তন নির্ণয় না করেও অন্য কোন উপায়ে নিচের ছবির আয়তাকার ঘনবস্তু দুটির আয়তনের অনুপাত নির্ণয় করতে পারো কিনা?
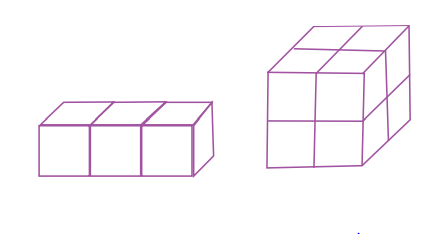
অনুপাত ও শতকরা:

উপরের চিত্রগুলোর (ক)চিত্রে, ১/8 অংশ, (খ)চিত্রে, ৩/৫ অংশ, (গ) চিত্রে, ৩/১০অংশ ছাই রঙ করা হয়েছে।
এখানে আমরা দেখতে পাই,
(ক) চিত্রে রঙ করা অংশ ও সম্পূর্ণ অংশের অনুপাত ১:৪ = ১/৪ = ১×২৫/৪×২৫ = ২৫/১০০ = ২৫%
(খ) চিত্রে রঙ করা অংশ ও সম্পূর্ণ অংশের অনুপাত ৩:৫ = ৩/৫ = ৩×২০/৫×২০ = ৬০/১০০ = ৬০%
(ক) চিত্রে রঙ করা অংশ ও সম্পূর্ণ অংশের অনুপাত ৩:১০ = ৩/১০ = ৩×১০/১০×১০ = ৩০/১০০ = ৩০%
সমস্যাঃ
জেসমিন ও আবিদার বর্তমান বয়সের অনুপাত ৩:২ এবং আবিদা ও আনিকার বর্তমান বয়সের অনুপাত ৫:১। আনিকার বর্তমান বয়স ৩ বছর ৬ মাস।
(ক) প্রথম অনুপাতকে শতকরায় প্রকাশ করো।
(খ) ৫ বছর পর আবিদার বয়স কত হবে?
(গ) আনিকার বর্তমান বয়স জেসমিনের বর্তমান বয়সের শতকরা কত ভাগ?
সমাধানঃ
(ক) প্রথম অনুপাত = ৩:২ = ৩×৫০/২×৫০ = ১৫০/১০০ = ১৫০%
(খ) আবিদার বর্তমান বয়স : আনিকার বর্তমান বয়স = ৫:১
অর্থাৎ, আবিদার বর্তমান বয়স, আনিকার বর্তমান বয়সের ৫ গুণ
আনিকার বর্তমান বয়স = ৩ বছর ৬ মাস
= (৩×১২+৬) মাস (‘.’ ১ বছর = ১২ মাস)
= (৩৬+৬) মাস
= ৪২ মাস
সুতরাং আবিদার বর্তমান বয়স = (৪২×৫) মাস
= ২১০ মাস
= ১৭ ১/২ বছর
তাহলে, ৫ বছর পর আবিদার বয়স হবে = (১৭ ১/২ + ৫) বছর = ২২ ১/২ বছর
(গ) জেসমিন ও আবিদার বর্তমান বয়সের অনুপাত=৩:৫
অর্থাৎ জেসমিনের বর্তমান বয়স = আবিদার বর্তমান বয়সের = ৩/২ গুন
“খ” হতে আবিদার বর্তমান বয়স= ১৭ ১/২ × ৩/২ বছর
= ৩৫/২ × ৩/২ বছর = ১০৫/৪ বছর = ২৬ ১/৪ বছর
আনিকার বর্তমান বয়স =৩ বছর ৬ মাস
= ৩৬/১২ বছর = ৩১/২ বছর = ৭/২ বছর
আনিকার বর্তমান বয়স জেসমিনের বর্তমান বয়সের
= ( ৭/২ /২৬ ১/৪) অংশ = (৭/২ × ১৪/১০৫) অংশ = (২ × ১০০/১৫) % = ৪০/৩ % = ১৩ ১/৩ %
অতএব, আনিকার বর্তমান বয়স জেসমিনের বর্তমান বয়সের ১৩ ১/৩ %
উদাহরণ:
দুইটি রাশির যোগফল ২৪০। তাদের অনুপাত ১: ৩ হলে, রাশি দুইটি নির্ণয় করো। ১ম রাশি ২য় রাশির শতকরা কত অংশ?
সমাধান:
রাশি দুইটির যোগফল = ২৪০
তাদের অনুপাত = ১: ৩
অনুপাতের রাশি দুইটির যোগফল = ১ + ৩ = ৪
১ম রাশি। = ২৪০ এর ১/৪ অংশ = ৬০
২য় রাশি = ২৪০ এর ৩/৪ অংশ = ১৮০
আবার, রাশি দুইটির অনুপাত = ১:৩
১ম রাশি, ২য় রাশির ১/৩ = (১×১০০)/(৩×১০০) = ১০০/৩ × ১/১০০ = ১০০/৩% = ৩৩ ১/৩%
সমস্যা:
কলার দাম ১৪২/৭ % কমে যাওয়ায় ৪২০ টাকায় পূর্বাপেক্ষা ১০ টি কলা বেশি পাওয়া যায়।
(ক) একটি সংখ্যার ১৪২/৭ % = ১০ হলে, সংখ্যাটি নির্ণয় করো।
(খ) প্রতি ডজন কলার বর্তমান দাম কত?
(গ) প্রতি ডজন কলা কত দামে বিক্রয় করলে ৩৩% লাভ হতো
সমানুপাত
বিদ্যালয়ের ছবি মাপি
তোমাদের বিদ্যালয়ের যে দালান/কাঠামো রয়েছে, সেটির প্রস্থ ও উচ্চতা নির্ণয় করতে হবে। প্রথমেই সেটির প্রস্থ মেপে সেটি লেখো।
এবার ভেবে দেখো তো উচ্চতা কীভাবে নির্ণয় করা যেতে পারে?

নিজেদের মাঝে মাপামাপি
এবার তোমরা সবাই কয়েকটি দলে ভাগ হয়ে নিজদের উচ্চতা ও ওজন মাপবে। প্রত্যেকের জন্য মেপে যে উচ্চতা ও ওজন পাও সেটি একটি ছকে লিপিবদ্ধ করো। এখানে তোমরা উচ্চতাটি সেন্টিমিটারে এবং ওজন কিলোগ্রাম এককে নির্ণয় করবে। এবার তোমাদের নিজেদের দলগতভাবে কাজটি হলে বাকি দলের সাথে সমন্বয় করে সকলের উচ্চতা ও ওজনের যে তথ্য পাওয়া যায় সেটি নিজেদের খাতায় লিপিবদ্ধ করো।
তোমাদের শ্রেণির সকলের তথ্য লিপিবদ্ধ করা হলে, তোমরা প্রত্যেকের উচ্চতা ও ওজনের অনুপাত নির্ণয় করো।

এবার, যাদের উচ্চতা ও ওজনের অনুপাত সমান অথবা কাছাকাছি, তাদের চিহ্নিত করে খাতায় গুচ্ছাকারে লিখো এবং তাদের একত্রে দলে ভাগ করে ফেলো।
তোমরা কি আমাদের জাতীয় স্মৃতিসৌধ দেখেছো? দেখো, নিচের চিত্রগুলো আমাদের জাতীয় স্মৃতিসৌধের।
এবার নিচের চিত্রগুলোর উচ্চতা ও প্রস্থ মেপে নিচের ছকে লিখো এবং সেগুলোর অনুপাত নির্ণয় করো।
চিত্রগুলো থেকে কী বুঝতে পারলে? চিত্রগুলোর অনুপাত কি সমান?
নিচের জিরাফগুলোকে কি দেখতে পারছো তোমরা? প্রথম জিরাফটির গলা ও পুরো দেহের দৈর্ঘ্যের অনুপাত কিন্তু তোমরা মেপে দেখেছো। এবার দেখো তো বাকি জিরাফগুলোর গলা ও পুরো দেহের দৈর্ঘ্যের অনুপাত কি সমান হয় কিনা। মেপে নিচের ছকটি পূরণ করে ফেলো।
এই ছকটি থেকে তোমাদের কি মনে হয়? জিরাফগুলোর অনুপাত কি সমান?
অনুপাত নির্ণয় করো।
(১) (এখানে চিত্রের ন্যায় ছবিগুলো হবে) [স্মৃতিসৌধের মত ৪ টা আমগাছের সমানুপাতিক ছবি হবে। ]
(২) (এখানে চিত্রের ন্যায় ছবিগুলো হবে) ফুটবলের ৪ টি গোলপোস্টের ছবি থাকবে। কোনটাই সমানুপাতিক না। একেকটি একেকরকম। তবে প্রতিটির দৈর্ঘ্য ও প্রস্থ অবশ্যই পূর্ণ সংখ্যা হবে। স্মৃতিসৌধের চিত্রের ন্যায় প্রস্থ ও দৈর্ঘ্য বুঝানোর জন্য তীরচিহ্ন থাকবে।
শিক্ষার্থীরা চলো আমরা একটি গল্প পড়ি।।
জ্যোতি ও বিথি দুই বোন। তারা মার্বেল খেলতে খুব পছন্দ করে। কিন্তু একদিন খেলার পর দেখা গেল তাদের সব মার্বেল হারিয়ে গেছে। পরেরদিন স্কুল থেকে ফেরার পথে দুজনেই আলাদাভাবে মার্বেল কিনলো। বাসায় এসে তারা দুজন জানতে পারলো জ্যোতি ৩০ টি মার্বেল ৫০ টাকা দিয়ে কিনেছে। অপরদিকে বিথি ২০ টি মার্বেল কিনেছে ৩০ টাকা দিয়ে। এখন চিন্তা করো তো তারা দুজনেই কি একই অনুপাতে দাম দিয়েছে কীনা?
ভেবে দেখো জ্যোতির মার্বেল ও দামের অনুপাত হয় ৩০ : ৫০ বা ৩ : ৫।
আবার বিথির মার্বেল ও দামের অনুপাত হয় ২০ : 30 বা 2 : 3
তাহলে দেখা যাচ্ছে দুজনের অনুপাত কিন্তু সময় নয়। তাই তারা কিন্তু একই অনুপাতে দাম দেয় নি।
এবার চলো আরেকটি গল্প নিয়ে চিন্তা করি।

মৌ এর কাছে ৩৬ টি টেনিস বল আছে, অপরদিকে সুব্রতর কাছে ১১২ টি টেবিল টেনিস বল আছে। তারা ঠিক করলো নিজেদের মাঝে টেনিস বল ও টেবিল টেনিস বল ভাগ করবে। এজন্য মৌ সুব্রতকে ১৮ টি টেনিস বল দিল অপরদিকে সুব্রত মৌকে ৫৬ টি টেবিল টেনিস বল দিল। ভেবে বলো তো দুজনের মাঝে টেনিস বল আর টেবিল টেনিস বলের সমবন্টন হয়েছে কীনা?
এখানে দেখো, মৌ এর কাছে আগে টেনিস বল ছিল ৩৬ টি এবং সে সুব্রতকে দেয় ১৮ টি। তাহলে তার সুব্রতকে দেয়া টেনিস বল সংখ্যা এবং তার প্রথমে থাকা টেনিস বল সংখ্যার অনুপাত হলো ১৮ : ৩৬ বা ১ : ২
আবার সুব্রতর কাছে আগে টেবিল টেনিস বল ছিল ১১২ টি এবং সে মৌকে দিয়ে দেয় ৫৬ টি। তাহলে তার মৌকে দেয়া টেবিল টেনিস বল সংখ্যা এবং তার প্রথমে থাকা টেবিল টেনিস বল সংখ্যার অনুপাত হলো ৫৬ : ১১২ বা ১ : ২।
এখানে দেখো, আরেকটি বিষয় কিন্তু চিন্তা করা যায়। ভাগাভাগি করার পর মৌ এর কাছে থাকা টেনিস বল ও টেবিল টেনিস বল অনুপাত দেখার চেষ্টা করি। সেটি হল ১৮ : ৫৬ বা ৯ : ২৮।
আবার সুব্রতর ক্ষেত্রে এ অনুপাতটি হয় ১৮ : ৫৬ বা ৯ : ২৮।
যেহেতু উভয়েই একই অনুপাতে নিজেদের মধ্যে জিনিস ভাগাভাগি করেছে এবং ভাগাভাগির পর দেখা যাচ্ছে তাদের কাছে থাকা বলগুলোর অনুপাত সমান। তাই বলা যায় দুজনের মাঝে টেনিস বল আর টেবিল টেনিস বলের সমবন্টন হয়েছে।
তিনটি বিদ্যালয়ের আমগাছ থেকে আম পাড়ার পর প্রতি ক্লাসের শিক্ষার্থীদের আম দেয়া হয়েছে। নিম্নোক্ত উপায়ে সেই আমগুলো দেয়া হয়েছে।

১ম বিদ্যালয়ে;

২য় বিদ্যালয়ে;

৩য় বিদ্যালয়ে;

এটির প্রেক্ষিতে নিচের প্রশ্নগুলোর উত্তর দাওঃ
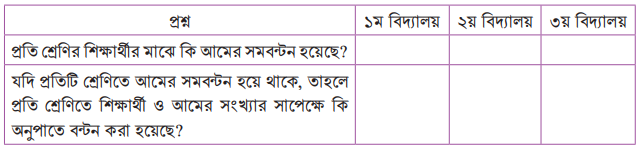
৩য় বিদ্যালয়ের শিক্ষার্থীদের শ্রেণিভিত্তিতে আম এমনভাবে পরিবর্তন করে নিচের ছক পূরণ করো যেন ১ম ও ৩য় বিদ্যালয়ের শিক্ষার্থীরা শ্রেণিভেদে সমান আম পায়ঃ

২য় বিদ্যালয়ের শিক্ষার্থীদের প্রাপ্ত আমের তথ্য অপরিবর্তিত রেখে ১ম ও ৩য় বিদ্যালয়ের শিক্ষার্থীদের শ্রেণিভিত্তিক প্রাপ্ত আমসংখ্যা এমনভাবে পরিবর্তন করে নিচের ছক পূরণ করো যেন ১ম ও ৩য় বিদ্যালয়ের শিক্ষার্থীরা শ্রেণিভেদে সমান আম পায়
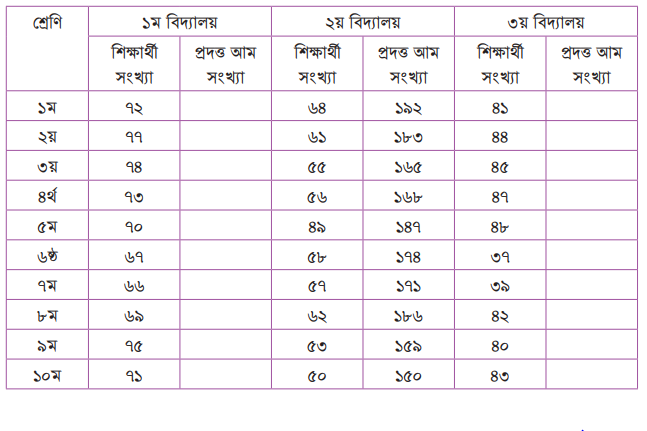
আমাদের জাতীয় পতাকা তৈরি করি
প্রিয় শিক্ষার্থীরা, চলো এবার আমরা আমাদের দেশের পতাকা সম্পর্কে জানি এবং একটি মজার কাজ করি। তোমরা সকলেই বাংলাদেশের পতাকা চেনো। নিচের বিভিন্ন স্থানে ব্যবহারের জন্য বাংলাদেশের পতাকার যে আকৃতি হয়, তা আংশিকভাবে দেয়া রয়েছে। তোমরা এবার সেটি পূরণ করার চেষ্টা করো।

এটি মূলত আমাদের জাতীয় পতাকার দৈর্ঘ্য ও প্রস্থের অনুপাত। এখন চিন্তা করো এই লাল বৃত্তটির কেন্দ্র কোথায় হবে?
এক্ষেত্রে নিয়মটি হল, বাম দিক থেকে পতাকার মোট দৈর্ঘ্যের ২০ ভাগের ৯ ভাগ বা ৯/২০ অংশ থেকে লম্বালম্বি ২০ বা প্রস্থ বরাবর একটি দাগ টানতে হবে। এবার পতাকার প্রস্থের অর্ধেক বা ১/২ অংশ থেকে পাশাপাশি বা দৈর্ঘ্য বরাবর একটি দাগ টানতে হবে। এই দুটি দাগ যে বিন্দুতে গিয়ে মিলেছে, সেটিই হল বৃত্তটির কেন্দ্রবিন্দু। সেই বিন্দুটিকে কেন্দ্র ধরে বৃত্তটি অঙ্কন করতে হবে।
এবার তাহলে তোমার উপরে সম্পূর্ণ করে আসা ছকের সাহায্য নিয়ে নিচের ছকটি সম্পূর্ণ করো। তোমাদের সুবিধার্থে ছকটির একটি সারি পূরণ করে দেয়া রয়েছে।

তিনটি দলে বিভক্ত হয়ে ৩, ৪, ৫ নং আকারে কাগজ কেটে জাতীয় পতাকার ন্যায় আয়তাকৃতিক কাগজ কাটো। তারপর পতাকার লাল বৃত্তের কেন্দ্রবিন্দু নির্ণয় করো। এরপর নির্দিষ্ট ব্যাসার্ধে বৃত্তটি অঙ্কন করো। পরবর্তীতে প্রয়োজনীয় রঙ ব্যবহার করে পতাকা বানানোর কাজটি সম্পন্ন করো।
এবার তোমাদের বানানো পতাকা তিনটি পাশাপাশি একটি টেবিল/বেঞ্চের উপর রাখো। পতাকাগুলো দেখে কি মনে হচ্ছে? সবগুলোর গড়ন কি একইরকম লাগছে?
এবার নিজেদের খাতায় উপরের ছকে পাওয়া পতাকার দৈর্ঘ্য ও প্রস্থের অনুপাতগুলোকে একটি নির্দিষ্ট অনুপাতে লেখো। লিখে দেখো যে দৈর্ঘ্য ও প্রস্থের অনুপাত একই হয় কিনা।
উপরের কর্মকান্ড হতে আমরা কী শিখলাম?
যদি দুই বা ততোধিক অনুপাত সমান হয় তবে সেই সকল সমান অনুপাতকে পরস্পরের সাপেক্ষে সমানুপাত বলা হয়।
দুইটি অনুপাত সমান হলে অর্থাৎ, সমানুপাত আকারে থাকলে সেই অনুপাত দুটির ১ম ও ৪র্থ পদকে | প্রান্তীয় পদ বলা হয় এবং ২য় ও ৩য় পদকে মধ্যপদ বলা হয়। অর্থাৎ, প্রথম অনুপাতের পূর্ব পদ এবং ২য় | অনুপাতের উত্তর পদ হল প্রান্তীয় পদ এবং ১ম অনুপাতের উত্তর পদ ও ২য় অনুপাতের পূর্ব পদ হল মধ্য পদ।
চিত্র ও বক্সের মাধ্যমে দুটি অনুপাত দেখিয়ে প্রান্তীয় ও মধ্যপদ দেখাতে হবে।
সমানুপাতকে সাধারণত = চিহ্ন এর বদলে :: চিহ্ন, অথবা α চিহ্ন দ্বারা প্রকাশ করা হয়।
যেমন ধরো, দুটি অনুপাত রয়েছে ১২ : ১৬ ও ৪৫ : ৬০।
এক্ষেত্রে অনুপাত দুটিকে লঘু করা হলে আমরা পাই ১২/১৬ = ৩/৪ এবং ৪৫/৬০ = ৩/৪
অর্থাৎ, বলা যায় এ দুটি রাশি সমানুপাতে আছে। তাহলে লেখা যায়, ১২ : ১৬ :: ৪৫ : ৬০
অথবা, ১২/১৬ α ৪৫/৬০
