আজকে আমরা অসমতার ধারণা সম্পর্কে আলোচনা করবো । যা উচ্চতর গণিতের সমীকরণ অংশের অন্তর্গত।

অসমতার ধারণা
মনে করি একটি ক্লাসের ছাত্রসংখ্যা 200 জন। স্বাভাবিকভাবে দেখা যায় যে, ঐ ক্লাসে সবদিন সকলে উপস্থিত থাকে না, সকলে অনুপস্থিতও থাকে না। একটি নির্দিষ্ট দিনে উপস্থিত ছাত্র সংখ্যা : হলে আমরা লিখতে পারি 0 << 200। একইভাবে আমরা দেখি যে, কোনো নিমন্ত্রিত অনুষ্ঠানেই সবাই উপস্থিত হয় না। পোশাক-পরিচ্ছদ ও অন্যান্য অনেক ভোগ্যপণ্য তৈরিতে পরিষ্কারভাবে অসমতার ধারণা প্রয়োজন হয়। দালান তৈরির ক্ষেত্রে, পুস্তক মুদ্রণের ক্ষেত্রে এবং এরকম আরও অনেক ক্ষেত্রে উপাদানগুলো সঠিক পরিমাণে নির্ণয় করা যায় না বিধায় প্রথম পর্যায়ে অনুমানের ভিত্তিতে উপাদানগুলো ক্রয় বা সংগ্রহ করতে হয়। অতএব দেখা যাচ্ছে যে, আমাদের দৈনন্দিন জীবনে অসমতার ধারণাটা খুবই গুরুত্বপূর্ণ।
বাস্তব সংখ্যার ক্ষেত্রে
a > b যদি ও কেবল যদি (a – b) ধনাত্মক অর্থাৎ (a – b) > 0
a < b যদি ও কেবল যদি (a – b) ঋণাত্মক অর্থাৎ (a – b) < 0
অসমতার কয়েকটি বিধি :
ক) a<b⇔b> a
খ) a> b হলে যেকোনো এর জন্য
a+c>b+c এবং a-c>b-c
গ) a> b হলে যেকোনো c এর জন্য
ac > bc এবং a/c> b/c যখন c> 0
ac < bc এবং a/c < b/c যখন c< 0
উদাহরণ ১.
x < 2 হলে
ক) x + 2 < 4 [উভয়পক্ষে 2 যোগ করে ]
খ) x – 2 < 0 [উভয়পক্ষে 2 বিয়োগ করে]
গ) 2x < 4 [উভয়পক্ষকে 2 দ্বারা গুণ করে]
ঘ) – 3x > – 6 [উভয়পক্ষকে – 3 দ্বারা গুণ করে
এখানে উল্লেখ্য যে,
a ≥ b এর অর্থ a > b অথবা a = b
a ≤ b এর অর্থ a < b অথবা a = b
a < b < c এর অর্থ a < b এবং b < c যার অর্থ a <c

উদাহরণ ২.
3 ≥ 1 সত্য যেহেতু 3 > 1
2 ≤ 4 সত্য যেহেতু 2 < 4
2 <3 < 4 সত্য যেহেতু 2 < 3 এবং 3 – 4
উদাহরণ ৩.
সমাধান কর ও সমাধান সেটটি সংখ্যারেখায় দেখাও: 4x + 4 > 16
সমাধান:
দেওয়া আছে, 4x + 4 > 16
বা, 4x + 4 – 4 > 164 [ উভয়পক্ষ থেকে 4 বিয়োগ করে
বা, x > 12
বা, 4.x 12 > [উভয়পক্ষকে 4 দ্বারা ভাগ করে]
বা, x > 3
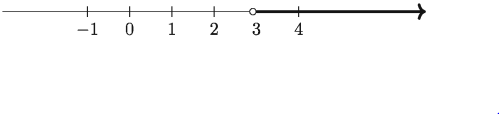
. নির্ণেয় সমাধান = > 3
এখানে সমাধান সেট, S = = {x ∈ R = x > 3}
সমাধান সেটটি নিচে অঙ্কিত সংখ্যারেখায় দেখানো হলো।
উদাহরণ ৪.
সমাধান কর এবং সমাধান সেট সংখ্যারেখায় দেখাও: x – 9 > 3x + 1
সমাধান:
দেওয়া আছে, – 9 > 3x + 1
বা, x – 9+ 9 > 3x + 1 + 9
বা, x > 3x + 10
বা, x – 3x > 3x + 10 – 3x
বা, – 2x > 10
বা, -2x/-2 < 10 /-2 [উভয়পক্ষকে – 2 দ্বারা ভাগ করায় অসমতার দিক পাল্টে গেছে]
বা, x < – 5
.:. নির্ণেয় সমাধান < – 5
সমাধান সেটটি নিচে অঙ্কিত সংখ্যা রেখায় দেখানো হলো।
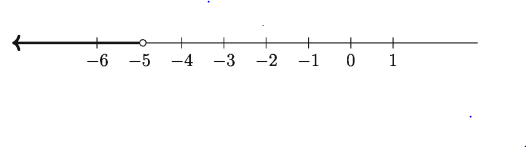
বিশেষ দ্রষ্টব্য:
সমীকরণের সমাধান যেমন একটি সমীকরণ (সমতা) দ্বারা প্রকাশ পায়, তেমনি অসমতার সমাধান একটি অসমতা দ্বারা প্রকাশ পায়। অসমতার সমাধান সেট (সাধারণত) বাস্তব সংখ্যার অসীম উপসেট।
উদাহরণ ৫.
সমাধান কর: a (x + b) < c [a ≠ 0]
সমাধান:
a ধনাত্মক হলে, a(x+b)/a <a /с [উভয়পক্ষকে a দ্বারা ভাগ করে]
বা, x + b < c/ a
a ঋণাত্মক হলে একই প্রক্রিয়ায় পাই, a(x+b) /a > c/ a
বা, x + b > c/ a
বা, x > c/ a – b
.:. নির্ণেয় সমাধান: (i) x < c/ a- b যদি a > 0 হয়,
(ii) x > c/ a- b যদি a < 0 হয়।
বিশেষ দ্রষ্টব্য:
a যদি শূন্য এবং c যদি ধনাত্মক হয়, তবে এর যেকোনো মানের জন্য অসমতাটি সত্য a হবে। কিন্তু a যদি শূন্য এবং ঋণাত্মক হয়, তবে অসমতাটির কোনো সমাধান থাকবে না।
অনুশীলনী
অসমতাগুলো সমাধান কর এবং সংখ্যারেখায় সমাধান সেট দেখাও :
১.y-3<5
২. 3 (x – 2 ) < 6
৩. 3x – 2 > 2x – 1
৪. z ≤ 1/2z +3
৫. 8 ≥ 2 -2x
৬. x≤x/4+4
৭. 5(3-2t) ≤ 3(4-3t)
৮. x/3 +x/4 +x/5 >47/60
