আজকে আমরা আলোচনা করবো এক এক ফাংশন সম্পর্কে । যা উচ্চতর গণিতের সেট ও ফাংশন অংশের অন্তর্গত।
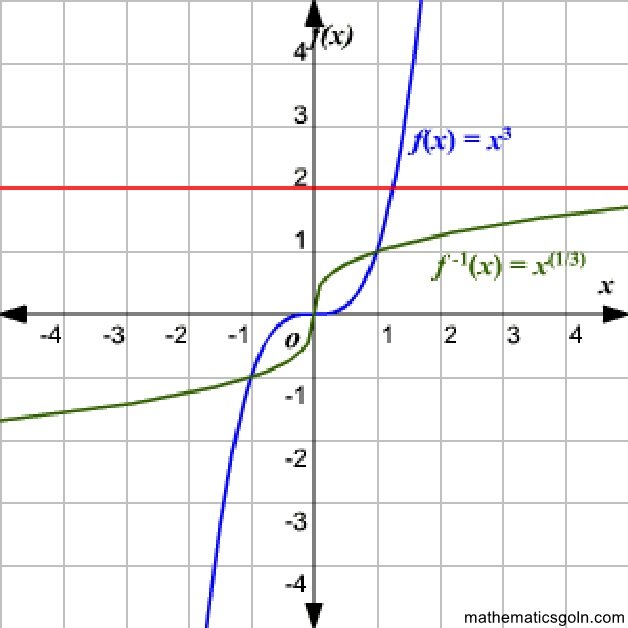
এক এক ফাংশন (One One Function)
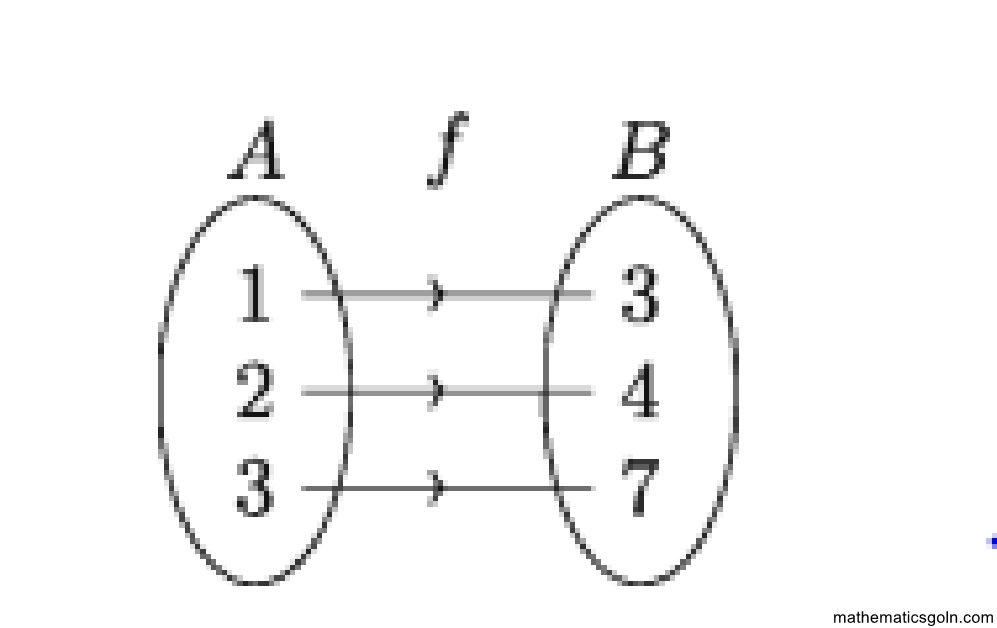
নিচের ভেনচিত্রে f ফাংশনের অধীনে ভিন্ন ভিন্ন সদস্যের প্রতিবিম্ব সর্বদা ভিন্ন।
সংজ্ঞা ১০ (এক-এক ফাংশন)
যদি কোন ফাংশন f এর অধীনে এর ডোমেনের ভিন্ন ভিন্ন সদস্যের প্রতিবিম্ব সর্বদা ভিন্ন হয়, তবে ফাংশনটিকে এক-এক (one-one) ফাংশন বলা হয়। অর্থাৎ X1, X2 ∈ ডোম f এবং X1 ≠ X2 হলে f(x1) ≠ f(x2)।
উপরের সংজ্ঞা থেকে দেখা যায়, একটি ফাংশন f : A→ B এক-এক ফাংশন হবে, যদি ও কেবল যদি f(x1) = f(x2) হলে x1 = x2 হয় যেখানে X1, X2 ∈ A।
উদাহরণ ৩০.
f(x) = 3x + 5, x ∈ R ফাংশনটি কি এক এক ফাংশন?
সমাধান:
মনে করি a,b∈ R এবং f(a) = f(b)।
তাহলে 3a + 5 = 3b + 5 বা, 3a. = 3b বা, a = b।
সুতরাং f ফাংশনটি এক-এক।
উদাহরণ ৩১.
দেখাও যে, F’ : R → R, F(x) = x2 ফাংশনটি এক-এক নয়।
সমাধান:
x1 = -1, x2: = 1 নিয়ে দেখি যে, x1 E ডোম F, x2 E ডোম F এবং X1 ≠ X2
কিন্তু F(x1) = F(−1) = (-1)2 = 1, F(x2) = F(1) = (1)2 = 1।
অর্থাৎ F(x1) = F(x2), .. F’ এক-এক নয়।
দ্রষ্টব্য: কোনো ফাংশনের বিপরীত অন্বয় ফাংশন নাও হতে পারে।
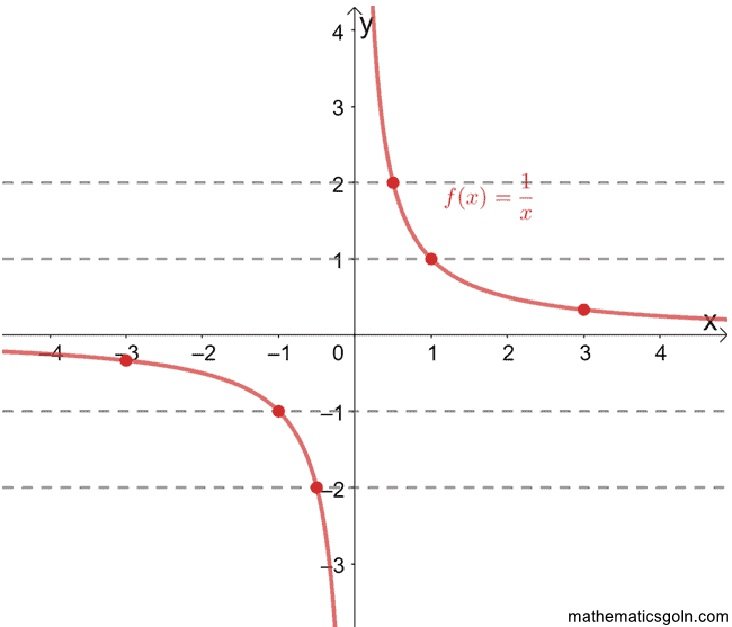
উদাহরণ ৩২.
f(x) = x/(x-2), x ≠ 2 বর্ণিত ফাংশনের জন্য নির্ণয় কর:
ক) f(5)
খ) f-1 (2)
সমাধান:
ক) f(x) = x/(x-2), x ≠ 2
f(5)= 5 /(5- 2)= 5/3
খ) ধরি, a = f-1 (2) তাহলে f(a) = 2
a /(a – 2) = 2
⇒ a = 2a – 4
⇒ a = 4
ƒ¹(2) = 4
উদাহরণ ৩৩.
f(x) = 3x + 1, 0 <x<2
ক) f এর রেঞ্জ নির্ণয় কর।
খ) দেখাও যে f এক-এক ফাংশন।
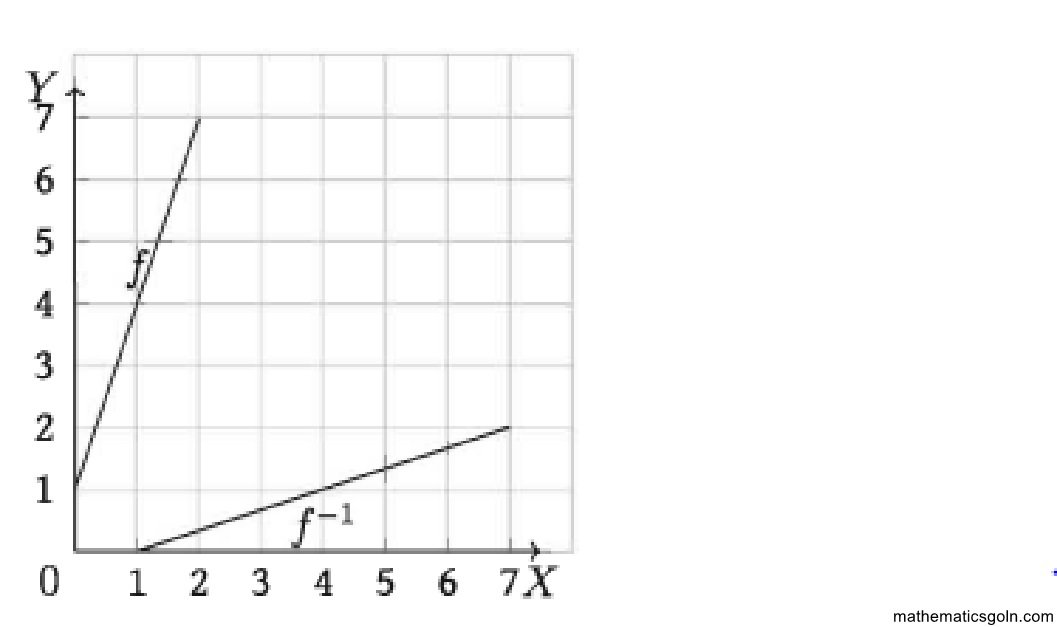
গ) f-1 নির্ণয় কর এবং f ও f-1 এর লেখচিত্র অঙ্কন কর।
সমাধান:
ক) f(x) = 3x + 1, 0 ≤ x ≤ 2 হতে পাই প্রান্ত বিন্দুদ্বয় (0, 1) এবং (2, 7 )
.:. রেঞ্জ f : R = {y: 1 <y <7}
খ) যেহেতু প্রত্যেক y ∈ R এর জন্য একমাত্র x ∈ {0 ≤ x ≤ 2} এর ইমেজ y দেখানো হয়েছে। সুতরাং f এক এক ফাংশন।
গ) ধরি, y = f(x), x এর ইমেজ।
তাহলে, y = 1 3x + 1 ⇒ x = = (-1) · 1 ) যা 1 (y-1) লেখচিত্রে দেখানো হয়েছে।
বিপরীত ফাংশন f−1 : y ⇒ x যেখানে, x = বা, f-1 : y → (y – 1) যা চিত্রে দেখানো হয়েছে।
y এর স্থলে x স্থাপন করে পাই, f-1 : x → 1/3 (x-1)
f-1 এর অঙ্কিত রেখা y = 1/3(x – 1), 1 ≤ x ≤7 দেখানো হয়েছে।

১ thought on “এক এক ফাংশন (One One Function)”