আজকে আমরা আয়তাকার কার্তেসীয় স্থানাঙ্ক সম্পর্কে আলোচনা করবো । যা উচ্চতর গণিতের স্থানাঙ্ক জ্যামিতি অংশের অন্তর্গত।

আয়তাকার কার্তেসীয় স্থানাঙ্ক
সমতলের ধারণা পূর্ববর্তী শ্রেণিতে দেওয়া হয়েছে। একটি টেবিলের উপরিভাগ, ঘরের মেঝে, বই-এর উপরিভাগ এমন কি যে কাগজের উপর লিখা হয় এদের প্রত্যেকেই সমতল। একটি ফুটবলের উপরিভাগ বা একটি বোতলের উপরিভাগ হলো বক্রতল। এই অংশে সমতলে অবস্থিত কোনো বিন্দুর সঠিক অবস্থান নির্ণয়ের কৌশল আলোচনা করা হবে। সমতলে অবস্থিত কোনো নির্দিষ্ট বিন্দুর সঠিক অবস্থান নির্ণয়ের জন্য ঐ সমতলে অঙ্কিত দুইটি পরস্পরছেদী সরলরেখা হতে নির্দিষ্ট বিন্দুর দূরত্ব জানা প্রয়োজন। এর কারণ হিসেবে বলা যায় পরস্পরছেদী দুইটি সরলরখা হতে কোনো নির্দিষ্ট দূরত্বে কেবলমাত্র একটি বিন্দুই থাকতে পারে।
কোনো সমতলে পরস্পর সমকোণে ছেদ করে এরূপ দুইটি সরলরেখা XOX’ এবং YOY’ আঁকলে XOX’ কে æ অক্ষ (x-axis), YOY’ কে y অক্ষ (y-axis) এবং ছেদ বিন্দু ‘O’ কে মূলবিন্দু (origin) বলা হয়।
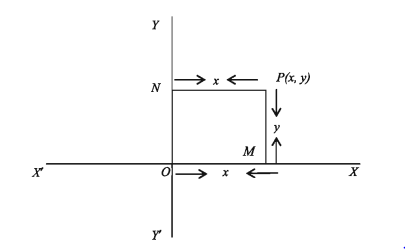
এখন ধরে নিই অক্ষদ্বয়ের সমতলে যেকোনো বিন্দু P। উক্ত P বিন্দু থেকে XOX’ অর্থাৎ, অক্ষ এবং YOY’ অর্থাৎ y অক্ষের উপর লম্ব যথাক্রমে PM এবং PN। তাহলে y অক্ষ হতে P বিন্দুর দূরত্ব = NP = OM = x কে P বিন্দুর ভুজ (abscissa) বা x স্থানাঙ্ক (x-coordinate) বলে । আবার x অক্ষ হতে P বিন্দুর দূরত্ব MP = ON = y কে P বিন্দুর কোটি (ordinate) বা y = স্থানাঙ্ক (y-coordinate) বলা হয়। ভুজ ও কোটিকে এক সাথে স্থানাঙ্ক বলা হয়। সুতরাং চিত্রে P বিন্দুর স্থানাঙ্ক বলতে y অক্ষ ও x অক্ষ হতে P বিন্দুর লম্ব দূরত্ব বোঝায় এবং তাদের x ও দ্বারা y নির্দেশ করে P বিন্দুর স্থানাঙ্ক P(x, y) প্রতীক দ্বারা প্রকাশ করা হয়।

বিন্দুর স্থানাঙ্ক সূচক (x, y) একটি ক্রমজোড় বুঝায় যার প্রথমটি ভুজ ও দ্বিতীয়টি কোটি নির্দেশ করে। তাই x ≠ y হলে (x, y) ও (y, x) দ্বারা দুইটি ভিন্ন বিন্দু বুঝায়। সুতরাং পরস্পর সমকোণে ছেদ করে এরূপ একজোড়া অক্ষের সাপেক্ষে কোনো বিন্দুর স্থানাঙ্ককে আয়তাকার কার্তেসীয় স্থানাঙ্ক বলা হয়। বিন্দুটি y অক্ষের ডানে থাকলে ভুজ ধনাত্মক ও বামে থাকলে ভুজ ঋণাত্মক হবে। আবার বিন্দুটি x অক্ষের উপরে থাকলে কোটি ধনাত্মক এবং নিচে থাকলে কোটি ঋণাত্মক হবে। x অক্ষের উপর কোটি শূন্য এবং y অক্ষের উপর ভুজ শূন্য হবে।
সুতরাং কোনো বিন্দুর ধনাত্মক ভুজ ও কোটি যথাক্রমে OX ও OY বরাবর বা তাদের সমান্তরাল দিকে থাকবে। একইভাবে ঋণাত্মক ভুজ ও কোটি OX’ ও OY’ বরাবর বা তাদের সমান্তরাল দিকে থাকবে।
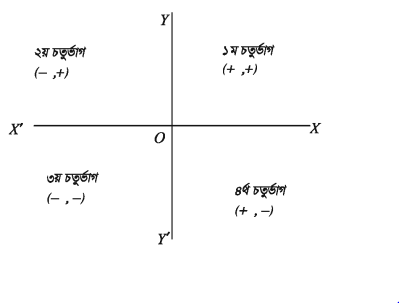
কার্তেসীয় স্থানাঙ্কের অক্ষদ্বয় দ্বারা সমতল XOY, Yox’, X’OY’, Y’OX এই চারটি ভাগে বিভক্ত হয়। এদের প্রত্যেকটিকে চতুর্ভাগ (quadrant) বলা হয়।
XOY চতুৰ্ভাগকে প্রথম ধরা হয় এবং ঘড়ির x কাঁটার আবর্তনের বিপরীত দিকে পর্যায়ক্রমে দ্বিতীয়, তৃতীয় ও চতুর্থ চতুর্ভাগ ধরা হয়। কোনো বিন্দুর স্থানাঙ্কের চিহ্ন অনুসারে বিন্দুর অবস্থান বিভিন্ন চতুর্ভাগে থাকে।

১ thought on “আয়তাকার কার্তেসীয় স্থানাঙ্ক ”