কোণ পরিমাপের একক

আজকে আমরা আলোচনা করবো কোণ পরিমাপের একক। যা উচ্চতর গণিতের ত্রিকোণমিতি অংশের অন্তর্গত।

 

 

কোণ পরিমাপের একক

কোনো কোণের পরিমাণ নির্ণয়ে সাধারণত দুই প্রকার পদ্ধতি ব্যবহার করা হয়:

ক) ষাটমূলক পদ্ধতি (Sexagesimal System) ও

খ) বৃত্তীয় পদ্ধতি (Circular System)

ষাটমূলক পদ্ধতি:

ষাটমূলক পদ্ধতিতে সমকোণকে কোণ পরিমাপের একক ধরা হয়। এই পদ্ধতিতে এক সমকোণকে সমান 90 ভাগে বিভক্ত করে প্রতি ভাগকে এক ডিগ্রী (1° = one degree) ধরা হয় ।

এক ডিগ্রিকে সমান 60 ভাগ করে প্রতিভাগকে এক মিনিট (1′ = one minute) এবং এক মিনিটকে সমান 60 ভাগ করে প্রতি ভাগকে এক সেকেন্ড (1″ = one second) ধরা হয়।

অর্থাৎ, 60” (সেকেন্ড) = 1′ (মিনিট)

60′ (মিনিট) = 1° (ডিগ্রি)

90° (ডিগ্রি) = 1 সমকোণ

বৃত্তীয় পদ্ধতি সম্পর্কে জানার পূর্বে রেডিয়ান সম্পর্কে জানা দরকার।

রেডিয়ান:

কোনো বৃত্তের ব্যাসার্ধের সমান চাপ ঐ বৃত্তের কেন্দ্রে যে কোণ উৎপন্ন করে সেই কোণকে এক রেডিয়ান বলে।

 

 

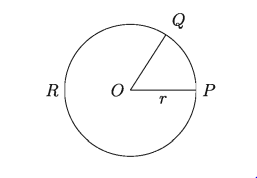
চিত্রে PQR বৃত্তের কেন্দ্র O, বৃত্তের ব্যাসার্ধ OP : = r এবং ব্যাসার্ধের সমান চাপ PQ । PQ চাপ কেন্দ্র O তে ŻPOQ উৎপন্ন করেছে। উক্ত কোণের পরিমাণই এক রেডিয়ান। অর্থাৎ ZPOQ এক রেডিয়ান।

বৃত্তীয় পদ্ধতি:

বৃত্তীয় পদ্ধতিতে এক রেডিয়ান (radian) কোণকে কোণ পরিমাপের একক ধরা হয়। কোণের ডিগ্রী পরিমাপ ও রেডিয়ান পরিমাপের সম্পর্ক নির্ণয়ের জন্য নিম্নোক্ত প্রতিজ্ঞাসমূহ এবং কোণের বৃত্তীয় পরিমাপ সম্পর্কে জানা প্রয়োজন।
প্রতিজ্ঞা ১. যেকোনো দুইটি বৃত্তের স্ব-স্ব পরিধি ও ব্যাসের অনুপাত সমান।

প্রমাণ:

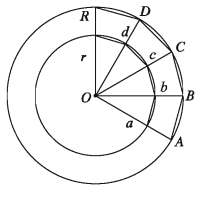
মনে করি, প্রদত্ত বৃত্ত দুইটি সমকেন্দ্রিক এবং উভয়ের কেন্দ্র O। বৃহত্তর বৃত্তটির পরিধি P ও ব্যাসার্ধ R এবং ক্ষুদ্রতর বৃত্তটির পরিধি p ও ব্যাসার্ধ (নিচের চিত্র)। এখন বৃহত্তর বৃত্তটিকে n সংখ্যক (n > 1) সমান ভাগে বিভক্ত করি। কেন্দ্রের সাথে বিভক্ত বিন্দুগুলো যোগ করলে ক্ষুদ্রতর বৃত্তটিও n সংখ্যক সমান ভাগে বিভক্ত হবে। উভয় বৃত্তে বিভক্ত বিন্দুগুলো পরস্পর সংযুক্ত করি। ফলে প্রত্যেক বৃত্তে n সংখ্যক বাহুবিশিষ্ট একটি সুষম বহুভুজ অন্তর্লিখিত হল (বৃহত্তর বৃত্তে ABCD… ও ক্ষুদ্রতর বৃত্তে abcd…).

এখন ∆OAB এবং ∆Oab সদৃশ, কারণ, ∠AOB এবং ∠aOb [সাধারণ কোণ] এবং উভয় ত্রিভুজ সমদ্বিবাহু বলে বাহু সংলগ্ন কোণগুলো সমান।

∴ AB/ ab = OA/ Oa =OB/Ob= R/r

 

 

অনুরূপভাবে,

∴ BC/ bc = R/r, CD /cd = ……….=R/r ইত্যাদি।

∴ AB/ ab = BC/ bc = CD /cd = ……….=R/r

∴ AB+BC+CD+… /ab + bc + cd … = R+R+R+… /r+r+r+… =  nR/ nr = R/r = 2R/2R .. (1)

n যদি যথেষ্ট বড় হয় (n = ∞) তাহলে AB, BC, CD,… রেখাংশসমূহ অত্যন্ত ক্ষুদ্র হবে এবং মনে হবে সবাই বৃত্তের ছোট ছোট চাপ।

সুতরাং এক্ষেত্রে, AB + BC + CD ………≉ বৃহত্তর বৃত্তের পরিধি P এবং
ab + bc + ad… ক্ষুদ্রতর বৃত্তের পরিধি p

∴ সমীকরণ (1) হতে পাই,

P /p= 2R/ 2r

অর্থাৎ, P /2R = p /2r

অর্থাৎ, বৃহত্তর বৃত্তের পরিধি /বৃহত্তর বৃত্তের ব্যাস = ক্ষুদ্রতর বৃত্তের পরিধি /ক্ষুদ্রতর বৃত্তের ব্যাস

যেকোনো দুইটি বৃত্তের পরিধি ও ব্যাসের অনুপাত সমান ।

প্রতিজ্ঞা ১ এর আলোকে মন্তব্য ও অনুসিদ্ধান্ত:

মন্তব্য:

যেকোনো বৃত্তের পরিধি ও ব্যাসের অনুপাত সবসময় সমান ও একই ধ্রুব সংখ্যা। এ ধ্রুব সংখ্যাটিকে গ্রিক বর্ণ ” (পাই) দ্বারা প্রকাশ করা হয়। য় একটি অমূলদ সংখ্যা এবং দশমিকে প্রকাশ π করলে এটি একটি অসীম দশমিক ভগ্নাংশ সংখ্যা ( π =  3.1415926535897932…).

মন্তব্য:

সাধারণত চার দশমিক স্থান পর্যন্ত ” এর আসন্ন মান ” = 3.1416 ব্যবহার করা হয়। কম্পিউটারের সাহায্যে ” এর মান এক লক্ষ কোটি দশমিক স্থান পর্যন্ত নির্ণীত হয়েছে। যেহেতু এর আসন্ন মান ব্যবহার করা হয় সেহেতু উত্তরও হবে আসন্ন। তাই উত্তরের পাশে ‘প্রায়’ লেখা অবশ্য কর্তব্য। পরবর্তী সমস্ত কাজে অন্য কোনোরূপ বলা না থাকলে চার দশমিক স্থান পর্যন্ত । এর আসন্ন
মান 3.1416 ব্যবহার করা হবে।

অনুসিদ্ধান্ত ২.

বৃত্তের ব্যাসার্ধ হলে, পরিধি হবে 2πr.

প্রমাণ: প্রতিজ্ঞা ১ এর আলোকে আমরা জানি,

পরিধি/ ব্যাস =π

বা, পরিধি = π ব্যাস

= π x 2r [ব্যাস = 2r]

= 2πr

ব্যাসার্ধ বিশিষ্ট যেকোনো বৃত্তের পরিধি 2πr.

প্রতিজ্ঞা ৩.

বৃত্তের কোনো চাপের উপর দন্ডায়মান কেন্দ্রস্থ কোণ ঐ বৃত্তচাপের সমানুপাতিক ।

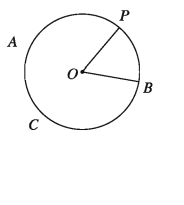
মনে করি, ABC বৃত্তের কেন্দ্র O এবং ব্যাসার্ধ OB । P বৃত্তের উপর অন্য একটি বিন্দু। ফলে BP বৃত্তের একটি চাপ এবং LPOB বৃত্তের একটি কেন্দ্রস্থ কোণ । তাহলে, কেন্দ্রস্থ ∠POB, চাপ BP এর সমানুপাতিক হবে। অর্থাৎ, কেন্দ্রস্থ ∠POB x চাপ BP.

 

 

প্রতিজ্ঞা ৪

রেডিয়ান কোণ একটি ধ্রুব কোণ ।

বিশেষ নির্বচন:

মনে করি, O কেন্দ্রবিশিষ্ট ABC বৃত্তে ∠POB এক রেডিয়ান কোণ। প্রমাণ করতে হবে যে, ∠POB একটি ধ্রুব কোণ।

অঙ্কন:

OB রেখাংশের (ব্যাসার্ধের) উপর OA লম্ব আঁকি।

 

 

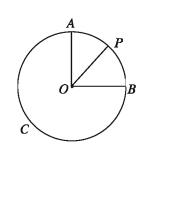
প্ৰমাণ:

OA লম্ব বৃত্তের পরিধিকে A বিন্দুতে ছেদ করে।

চাপ AB = পরিধির এক-চতুর্থাংশ =1 /4 x 2πr =  πr/2 = এবং চাপ PB = ব্যাসার্ধ r [∠POB = 1 রেডিয়ান] প্রতিজ্ঞা ৩ থেকে পাই,

∠POB/ ∠AOB = চাপ PB/ চাপ AB

∠POB = চাপ PB/ চাপ AB × ∠AOB

= r/(πr/2)  × এক সমকোণ [OA ব্যাসার্ধ এবং OB এর উপর  লম্ব]

= 2/π সমকোণ

যেহেতু সমকোণ ও π ধ্রুবক সেহেতু ∠ POB একটি ধ্রুব কোণ।

কোণের বৃত্তীয় পরিমাপ

সংজ্ঞা ১.

বৃত্তীয় পদ্ধতিতে (circular system) অর্থাৎ, রেডিয়ান এককে কোনো কোণের পরিমাপকে তার বৃত্তীয় পরিমাপ (circular measure) বলা হয়।

মনে করি, ∠MON যেকোনো একটি কোণ যার বৃত্তীয় পরিমাপ নির্ণয় করতে হবে। O বিন্দুকে কেন্দ্র করে OA = r ব্যাসার্ধ নিয়ে একটি বৃত্ত অঙ্কন করি। বৃত্তটি OM ও ON কে যথাক্রমে A ও B বিন্দুতে ছেদ করে। তাহলে AB চাপ দ্বারা উৎপন্ন কেন্দ্রস্থ কোণ ∠AOB। ব্যাসার্ধ r এর সমান করে AP চাপ নিই (চাপ ও ব্যাসার্ধ একই এককে হতে হবে)।

 

 

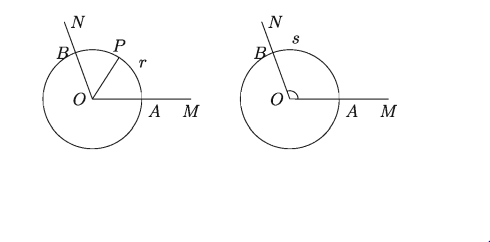
তাহলে, ∠AOP = 1 রেডিয়ান।

ধরি চাপ AB = s

প্রতিজ্ঞা ৩ অনুযায়ী,

∠MON/ ∠AOP =চাপ AB /চাপ AP = চাপ AB/ ব্যাসার্ধ OA = s/r

∠MON =  s/r x ∠AOP

s/r × 1 রেডিয়ান  = s/r রেডিয়ান

∠MON এর বৃত্তীয় পরিমাপ s/r, যেখানে কোণটি তার শীর্ষবিন্দুকে কেন্দ্র করে এবং r ব্যাসার্ধ নিয়ে অঙ্কিত বৃত্তে s পরিমাণ চাপ খন্ডিত করে।

প্রতিজ্ঞা ৫.

r ব্যাসার্ধের কোনো বৃত্তে s দৈর্ঘ্যের কোনো চাপ কেন্দ্রে ৪ পরিমাণ কোণ উৎপন্ন করলে s = r8 হবে।

 

 

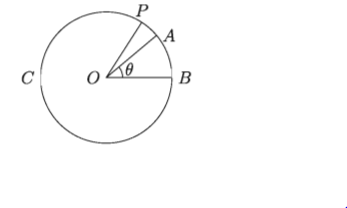
বিশেষ নির্বচন

মনে করি, O কেন্দ্রবিশিষ্ট ABC বৃত্তের ব্যাসার্ধ OB = একক, চাপ AB = 8 একক এবং AB চাপ দ্বারা উৎপন্ন কেন্দ্রস্থ ∠AOB= 8° ।

প্রমাণ করতে হবে যে, s = r8.

অঙ্কন:

B বিন্দুকে কেন্দ্র করে OB এর সমান ব্যাসার্ধ বিশিষ্ট BP চাপ আঁকি যেন তা ABC বৃত্তের পরিধিকে P বিন্দুতে ছেদ করে। O P যোগ করি।

প্রমাণ:

অঙ্কন অনুসারে ∠POB = 1c

আমরা জানি, কোনো বৃত্তচাপ দ্বারা উৎপন্ন কেন্দ্রস্থ কোণ ঐ বৃত্তচাপের সমানুপাতিক ।

চাপ AB /চাপ PB = ∠AOB /∠POB

বা, ৪ একক / r একক = 8°/1º

বা, s/r  = 8

বা, s = r8 (প্রমাণিত)

কোণের ডিগ্রি পরিমাপ ও রেডিয়ান (বৃত্তীয়) পরিমাপের সম্পর্ক

প্রতিজ্ঞা ৪ থেকে আমরা পাই,

1 রেডিয়ান = 2/π সমকোণ

অর্থাৎ, 1c = 2/π সমকোণ। [1 রেডিয়ান = 1c]

1 সমকোণ = (π/2)c

বা, 90° = (π/2)c

..1° =  (π/180)c  এবং 1c = (180/π)°

প্রতিজ্ঞা ৬.

1° = (π/180)c  এবং 1c = (180/π)°

লক্ষণীয়:

(i) 90° = 1 সমকোণ = π/2 রেডিয়ান = (π/2)c

অর্থাৎ, 180° = 2 সমকোণ = রেডিয়ান =πc

(ii) ষাটমুলক ও বৃত্তীয় পদ্ধতিতে একটি কোণের পরিমাপ যথাক্রমে D° ও Rc হলে

D° = ( D x π/180 )c =R

অর্থাৎ, D x π/180 = R

বা, D/ 180 = R/π

উপরোক্ত আলোচনা থেকে বহুল ব্যবহৃত কোণসমূহের ডিগ্রি ও রেডিয়ানের সম্পর্ক দেওয়া হলো:

(i) 1° = (π/180 )c

(ii) 30° – (30 × π/180)c = (π/6)c

(iii) 45° = (45 × π/180)c = (π/4)c

(iv) 60° = (60 × π/180)c = (π/3)c

(v) 90°= (90 × π/180)c = (π/2)c

(vi) 180° = (180 × π/180)c = (π)c

(vii) 360° = (360 × π/180)c = (2π)c

ব্যবহারিক ক্ষেত্রে রেডিয়ান প্রতীক (c) সাধারণত লিখা হয় না। সংক্ষেপে (রেডিয়ান প্রতীক উহ্য রেখে)

1° = 180, 30° = π/6, 45° = π/4,60° = π/3, 90° = π/2, 180° = π, 360° = 2π ইত্যাদি।

দ্রষ্টব্য:

1° = (π/180)c = 0.01745 (আসন্ন পাঁচ দশমিক স্থান পর্যন্ত)

1c = (180/π)°  = 57.29578° (আসন্ন পাঁচ দশমিক স্থান পর্যন্ত) = 57°1744.81″,

এক্ষেত্রে এর আসন্ন মান 3.1416 ব্যবহার করা হয়েছে।

দ্রষ্টব্য:

নিচের সমস্ত উদাহরণ এবং সমস্ত সমস্যায় এর আসন্ন মান চার দশমিক স্থান ( = 3.1416) পর্যন্ত ব্যবহার করা হবে। এর আসন্ন মান ব্যবহৃত হলে উত্তরে অবশ্যই ‘প্রায়’ কথাটি লিখতে হবে।

উদাহরণ ৩.

ক) 30°1236″ কে রেডিয়ানে প্রকাশ কর।

খ) 3π/13কে ডিগ্রি, মিনিট ও সেকেন্ডে 13 প্রকাশ কর।

সমাধান :

ক) 30°12′36″ = 30° (1236/60)’ -30° (123/5) =30° (63/5)’

={3063 /(5 x 60)}° = (3021/ 100)° = (3021/100)°

(3021 /100) x (π/180) রেডিয়ান [:.. 1° = πc/180]

= 3021π/ 18000 = .5273 রেডিয়ান (প্রায়)

30° 1236″ = .5273 (প্রায়)

খ) 3π/13 = (3π/13) x (π/180) ডিগ্রি [ : 1c = (180/π)°

= 540/13 ডিগ্রি =  41°32’18.46″.

3π/13  রেডিয়ান = 41° 32′ 18.46″

উদাহরণ ৪.

একটি ত্রিভুজের তিনটি কোণের অনুপাত 3 : 45, কোণ তিনটির বৃত্তীয় মান কত?

সমাধান:

ধরি, কোণ তিনটি যথাক্রমে 3xc, 4xc ও 5xc

প্রশ্নমতে,

3xc + 4xc + 5xc = πc [ত্রিভুজের তিন কোণের সমষ্টি 2 সমকোণ = πc]

বা, 12xc = πc

বা, x =  π/12

কোণ তিনটি যথাক্রমে

3xc = (3π/12)c  = (π/4)c

4xc = (4π/12)c  = (π/3)c

5xc = (5π/12)c  = (5π/12)c

নির্ণেয় কোণ তিনটির বৃত্তীয় মান : π/4, π/3, 5π/12

উদাহরণ ৫.

একটি চাকা 1.75 কিলোমিটার পথ যেতে 40 বার ঘুরে। চাকাটির ব্যাসার্ধ কত?

সমাধান:

ধরি, ঢাকার ব্যাসার্ধ r মিটার।

চাকার পরিধি = 2πr মিটার [ = 3.1416 ]

আমরা জানি, চাকাটি একবার ঘুরলে তার পরিধির সমান দূরত্ব অতিক্রম করে।

40 বার ঘুরায় চাকাটির মোট অতিক্রান্ত দূরত্ব = 40 x 2πr মি. = 80πr মিটার

প্রশ্নমতে, 80πr = 1750 [1.কি.মি. = 1000 মিটার]

বা, r = 1750/ 80π =  1750/ (80 x 3.1416) মিটার

= 6.963 মিটার (প্রায়)।

চাকার ব্যাসার্ধ 6.963 মিটার (প্রায়)।

উদাহরণ ৬.

পৃথিবীর ব্যাসার্ধ 6440 কিলোমিটার। ঢাকা ও জামালপুর পৃথিবীর কেন্দ্রে 2° কোণ উৎপন্ন করলে ঢাকা ও জামালপুরের দূরত্ব নির্ণয় কর।

সমাধান:

ব্যাসার্ধ ,r =6440 কি.মি.

পৃথিবীর কেন্দ্রে উৎপন্ন কোণ 8 = 2° = 2 x  πc/180 = π/90রেডিয়ান।

s = চাপের দৈর্ঘ্য = ঢাকা ও জামালপুরের দূরত্ব = r8 = 6440 x π/90 কি.মি.

= 644 x π/9 কি.মি.

= 224.8 কি.মি. (প্রায়)

নির্ণেয় দূরত্ব: 224.8 কি.মি. (প্রায়)।

উদাহরণ ৭.

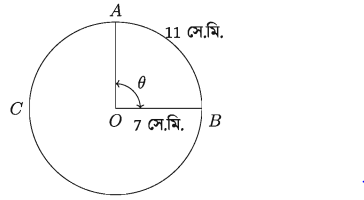
কোনো বৃত্তের ব্যাসার্ধ 7 সে.মি.। বৃত্তের 11 সে.মি. দীর্ঘ চাপের কেন্দ্রস্থ কোণের পরিমাণ নির্ণয় কর।

সমাধান:

ধরি, ABC বৃত্তের ব্যাসার্ধ OB = 7 সে.মি. এবং চাপ AB = 11 সে.মি.। AB চাপের = কেন্দ্রস্থ কোণের পরিমাণ ৪ নির্ণয় করতে হবে।

আমরা জানি, ৪ = s/r = 11 সে.মি. /7 সে.মি.

= 1.57 রেডিয়ান (প্রায়)

নির্ণেয় কোণের পরিমাণ: 1.57 রেডিয়ান (প্রায়)।

 

 

উদাহরণ ৮.

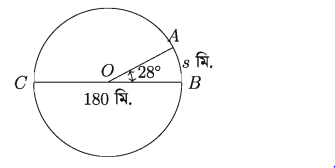
এহসান সাইকেলে চড়ে বৃত্তাকার পথে 10 সেকেন্ডে একটি বৃত্তচাপ অতিক্রম করে। যদি চাপটি কেন্দ্রে 28° কোণ উৎপন্ন করে এবং বৃত্তের ব্যাস 180 মিটার হয়, তবে এহসানের গতিবেগ নির্ণয় কর।

সমাধান:

ধরি, এহসান ABC বৃত্তের B বিন্দু থেকে যাত্রা করে 10 সেকেন্ড পরে পরিধির উপর A বিন্দুতে আসে।

তাহলে AB চাপ দ্বারা উৎপন্ন কেন্দ্রস্থ কোণ ∠AOB = 28°

OB = ব্যাসার্ধ = 180/ 2 মিটার = 90 মিটার

ধরি, চাপ AB = s মিটার

 

 

আমরা জানি,
s = r8

= 90 × 28 × π/180মিটার

= 14π মিটার

= 14 x 3.1416 মিটার (প্রায়)

= 43.98 মিটার (প্রায়)

এহসানের গতিবেগ = 43.9/10 মিটার/সেকেন্ড = 4.398 মিটার/সেকেন্ড = 4.4 মিটার/সেকেন্ড (প্রায়)

নির্ণেয় গতিবেগ: 4.4 মিটার/সেকেন্ড (প্রায়)

উদাহরণ ৯.

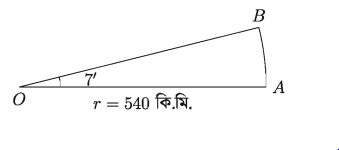
540 কিলোমিটার দূরে একটি বিন্দুতে কোনো পাহাড় ?’ কোণ উৎপন্ন করে। পাহাড়টির উচ্চতা নির্ণয় কর।

সমাধান:

মনে করি, AB পাহাড়টির পাদবিন্দু A থেকে 540 কি.মি. দূরে O বিন্দুতে পাহাড়টি 7′ কোণ উৎপন্ন করে।

তাহলে AO = r = ব্যাসার্ধ = 540 কি.মি.

কেন্দ্রস্থ কোণ ∠AOB = 7′ = (7/60)° = 7π/( 60 x 180) রেডিয়ান ।

পাহাড়ের উচ্চতা ≈ চাপ = s কি.মি.

 

 

আমরা জানি,

s = r8 = 540 x (7π/ 60 x 180) কি.মি.

= (7 x 3.1416 )/20 কি.মি. (প্রায়)

= 1.1 কি.মি. (প্রায়)

পাহাড়টির উচ্চতা 1.1 কি.মি. (প্রায়) বা 1100 মিটার (প্রায়)।