ক্ষেত্রফল সম্পর্কিত উপপাদ্য ও সম্পাদ্যের অনুশীলনী

আজকে আমরা ক্ষেত্রফল সম্পর্কিত উপপাদ্য ও সম্পাদ্যের অনুশীলনী আলোচনা করবো। এটি নবম – দশম শ্রেনী গণিতের ক্ষেত্রফল সম্পর্কিত উপপাদ্য ও সম্পাদ্য এর অন্তর্গত।

 

 

ক্ষেত্রফল সম্পর্কিত উপপাদ্য ও সম্পাদ্যের অনুশীলনী

১. ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য দেওয়া আছে; নিচের কোন ক্ষেত্রে সমকোণী ত্রিভুজ অঙ্কন সম্ভব নয়?

ক) 3 সে.মি., 4 সে.মি., 5 সে.মি.

খ) 6 সে.মি., ৪ সে.মি., 10 সে.মি.

গ) 5 সে.মি., 7 সে.মি., 9 সে.মি.

ঘ) 5 সে.মি., 12 সে.মি., 13 সে.মি.

২. সমতলীয় জ্যামিতিতে

(i) প্রত্যেক সীমাবদ্ধ সমতলক্ষেত্রের নির্দিষ্ট ক্ষেত্রফল রয়েছে

(ii) দুইটি  ত্রিভুজক্ষেত্রের ক্ষেত্রফল সমান হলেই ত্রিভুজ দুইটি সর্বসম

(iii) দুইটি ত্রিভুজ সর্বসম হলে এদের ক্ষেত্রফল সমান

নিচের কোনটি সঠিক?

ক) i ও ii

খ) i ও iii

গ) ii ও iii

ঘ) i, ii ও iii

পাশের চিত্রে, AABC সমবাহু, AD ⊥ BC এবং AB = 2

 

 

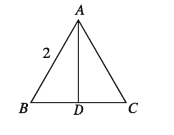
উপর্যুক্ত তথ্যের ভিত্তিতে ৩ ও ৪ নং প্রশ্নের উত্তর দাও :

BD =  কত?

ক) 1

খ) √2গ) 2

ঘ) 4

৪. ত্রিভুজটির উচ্চতা কত?

ক) 4 √3

খ) √3

গ) √3

ঘ) 2√3

৫. প্রমাণ কর যে, ত্রিভুজের যে কোনো মধ্যমা ত্রিভুজক্ষেত্রটিকে সমান ক্ষেত্রফল বিশিষ্ট দুইটি ত্রিভুজক্ষেত্রে বিভক্ত করে।

৬. প্রমাণ কর যে, কোনো বর্গক্ষেত্র তার কর্ণের উপর অঙ্কিত বর্গক্ষেত্রের অর্ধেক।

৭. প্রমাণ কর যে, সামান্তরিকের কর্ণদ্বয় সামান্তরিকক্ষেত্রটিকে চারটি সমান ত্রিভুজক্ষেত্রে বিভক্ত করে।

৮. একটি সামান্তরিকক্ষেত্র এবং সমান ক্ষেত্রফল বিশিষ্ট একটি আয়তক্ষেত্র একই ভূমির উপর এবং এর একই পাশে অবস্থিত। দেখাও যে, সামান্তরিকক্ষেত্রটির পরিসীমা আয়তক্ষেত্রটির পরিসীমা অপেক্ষা বৃহত্তর।

 

 

৯. ∆ABC এর AB ও AC বাহুদ্বয়ের মধ্যবিন্দু যথাক্রমে X ও Y। প্রমাণ কর যে, ∆AXY এর ক্ষেত্রফল = ∆ABC এর ক্ষেত্রফল।

১০. ABCD একটি ট্রাপিজিয়াম। এর AB ও CD বাহু দুইটি সমান্তরাল। ট্রাপিজিয়ামক্ষেত্র ABCD এর ক্ষেত্রফল নির্ণয় কর।

১১. সামান্তরিক ABCD এর অভ্যন্তরে P যেকোনো একটি বিন্দু। প্রমাণ কর যে, ∆PAB এর ক্ষেত্রফল + ∆PCD এর ক্ষেত্রফল = 1/2( সামান্তরিক্ষেত্র ABCD এর ক্ষেত্রফল)।

১২. ∆ABC এ BC ভূমির সমান্তরাল যেকোনো সরলরেখা AB ও AC বাহুকে যথাক্রমে D ও E বিন্দুতে ছেদ করে। প্রমাণ কর যে, ∆DBC = ∆EBC এবং ∆DBE = ∆CDE

১৩. ABC ত্রিভুজের ∠A  = এক সমকোণ। D, AC এর উপরস্থ একটি বিন্দু। প্রমাণ কর যে, BC2 + AD2 = BD2 + AC2 |

১৪. ABC একটি সমদ্বিবাহু সমকোণী ত্রিভুজ। BC এর অতিভুজ এবং P, BC এর উপর যেকোনো বিন্দু। প্রমাণ কর যে, PB2 + PC2 = 2PA2

১৫. ∆ABC এর ∠C স্থূলকোণ। AD, BC এর উপর লম্ব। দেখাও যে, AB2 = AC2 + BC2 + 2BC.CD

১৬. ∆ABC এর AC2 +C সূক্ষ্মকোণ। AD, BC এর উপর লম্ব। দেখাও যে, AB2 = AC2 + BC2 – 2BC.CD

১৭. APQR এ QD একটি মধ্যমা।

ক) উদ্দীপকের আলোকে আনুপাতিক চিত্র আঁক।

খ) প্রমাণ কর, PQ2 + QR2 = 2 ( PD2 + QD2)।

গ) যদি PQ = QR = PR হয়, তাহলে প্রমাণ কর, 4QD2 = 3PQ

 

১৮. ABCD সামান্তরিকের AB = 5 সে.মি., AD = 4 সে.মি. এবং ∠BAD = 75°। অপর একটি সামান্তরিক APML এর ∠LAP =  60°। ∠AED এর ক্ষেত্রফল ও APML = সামান্তরিকের ক্ষেত্রফল, ABCD সামান্তরিকের ক্ষেত্রফলের সমান।

ক) পেন্সিল, কম্পাস ও স্কেল ব্যবহার করে ∠BAD আঁক।

খ) ∆AED অঙ্কন কর। [অঙ্কন চিহ্ন ও বিবরণ আবশ্যক]।

গ) APML সামান্তরিকটি অঙ্কন কর। [অঙ্কন চিহ্ন ও বিবরণ আবশ্যক]।