আজকে আমরা ত্রিভুজক্ষেত্রের ক্ষেত্রফল সম্পর্কে আলোচনা করবো । যা উচ্চতর গণিতের স্থানাঙ্ক জ্যামিতি অংশের অন্তর্গত।

ত্রিভুজক্ষেত্রের ক্ষেত্রফল (Area of triangles)
আমরা জানি, তিনটি ভিন্ন বিন্দু একই সরলরেখায় অবস্থান না করলে ঐ তিনটি বিন্দুকে সরলরেখা দ্বারা যোগ করলে একটি ত্রিভুজক্ষেত্র পাওয়া যায়। উক্ত ত্রিভুজক্ষেত্রটি বাহুভেদে এবং কোণভেদে ভিন্ন ভিন্ন হতে পারে। এই অংশে আমরা একটি মাত্র সূত্রের সাহায্যে যেকোনো ত্রিভুজের বাহুর দৈর্ঘ্য নির্ণয়ের মাধ্যমে ত্রিভুজটির ক্ষেত্রফল নির্ণয় করতে সক্ষম হব। একই সূত্রের সাহায্যে যেকোনো চতুর্ভুজকে দুইটি ত্রিভুজ ক্ষেত্রে বিভক্ত করে চতুর্ভুজ ক্ষেত্রের ক্ষেত্রফল নির্ণয় করাও সম্ভব হবে।
এক্ষেত্রে আমরা ত্রিভুজ ক্ষেত্রটির পরিসীমা (বাহুগুলোর দৈর্ঘ্যের সমষ্টি) এবং বাহুর দৈর্ঘ্যের মাধ্যমে ক্ষেত্রফল নির্ণয় করব। যেকোনো ত্রিভুজ আকৃতি বা কোণাকৃতির জমির ক্ষেত্রফল নির্ণয়ের এই পদ্ধতি অর্থাৎ বাহুর দৈর্ঘ্যের মাধ্যমে ক্ষেত্রফল নির্ণয় অত্যন্ত গুরুত্বপূর্ণ। অর্থাৎ জমির ক্ষেত্রফল নির্ণয়ে এটি খুবই কার্যকর। কারণ হিসেবে বলা যায় ত্রিকোণাকার বা চৌকোণাকার জমির শীর্ষবিন্দুগুলোর স্থানাঙ্ক যদি জানা না থাকে বা সম্ভব না হয় কিন্তু যদি বাহুর দৈর্ঘ্য জানা থাকে তাহলেও আমরা ক্ষেত্রফল নির্ণয়ে সক্ষম হব। এই অংশে আমরা দুইটি পদ্ধতির মাধ্যমে ত্রিভুজ বা বহুভুজের ক্ষেত্রফল নির্ণয় করবো।

পদ্ধতি ১: বাহুর দৈর্ঘ্য ও পরিসীমার সাহায্যে ক্ষেত্রফল নির্ণয়
ক্ষেত্রফল নির্ণয়ের সূত্র:
পার্শ্বের চিত্রে ABC একটি ত্রিভুজ দেখানো হয়েছে। A (x1,y1), B(x2, y2) এবং C(x3, y3) তিনটি ভিন্ন বিন্দু এবং AB, BC ও CA ত্রিভুজের তিনটি বাহু। দূরত্ব নির্ণয়ের সূত্রের সাহায্যে সহজেই AB, BC ও CA বাহুর দৈর্ঘ্য নির্ণয় সম্ভব। যেমন:
AB বাহুর দৈর্ঘ্য ধরে C
C = √ {(x1 – x2 )2 + (y1 – y2)2} একক
BC বাহুর দৈর্ঘ্য a ধরে
a = √ {(x2 – x3)2 + (y2 – y3)2} একক
AC বাহুর দৈর্ঘ্য b ধরে
b = √{(x1 – x3)2 + (y1 – y3)2} একক

এখন ত্রিভুজটির পরিসীমা 2s ধরে
2s = a + b + c [পরিসীমা = বাহু তিনটির দৈর্ঘ্যের সমষ্টি]
অর্থাৎ s = 1/2(a + b + c) একক, এখানে ৪ হলো ত্রিভুজের পরিসীমার অর্ধেক।
আমরা s এবং a, b, c এর সাহায্যে সহজেই যেকোনো ত্রিভুজের ক্ষেত্রফল নির্ণয় করতে পারি।
ত্রিভুজ ক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সূত্র
ত্রিভুজ ABC এর AB বাহুর দৈর্ঘ্য c, BC বাহুর দৈর্ঘ্য a এবং CA বাহুর দৈর্ঘ্য b এবং পরিসীমা 2s হলে AABC এর ক্ষেত্রফল /s ( s – a) (s – b) (s – c) বর্গ একক [নবম-দশম শ্রেণির গণিত – বই এর পরিমিতি অংশে প্রমাণ দেওয়া আছে। শিক্ষার্থীরা প্রমাণটি দেখে নিবে।]
নিম্নোক্ত উদাহরণসমূহের মাধ্যমে সূত্রটির ব্যবহার সহজেই বুঝা যাবে।
লক্ষণীয়:
বিভিন্ন ত্রিভুজের ক্ষেত্রফল নির্ণয়ের বিভিন্ন সূত্র রয়েছে, কিন্তু একটি মাত্র সূত্রের সাহায্যে আমরা এখানে যেকোনো ত্রিভুজের ক্ষেত্রফল নির্ণয়ে সক্ষম হব।
উদাহরণ ৬.
একটি ত্রিভুজের তিনটি শীর্ষবিন্দু A (2, 5), B(- 1, 1 ) ও C(2, 1)। ত্রিভুজটির একটি মোটামুটি চিত্র আঁক এবং পরিসীমা ও বাহুর দৈর্ঘ্যের মাধ্যমে ক্ষেত্রফল নির্ণয় কর। ত্রিভুজটি কোন ধরনের ত্রিভুজ চিত্র দেখে আন্দাজ কর এবং তার সপক্ষে যুক্তি দাও।
সমাধান:
চিত্রে ত্রিভুজটির চিত্র দেখানো হলো।

AB বাহুর দৈর্ঘ্য, c=√{(−1 − 2)² + (1 − 5)²}
= √(9 + 16) = 5 একক
BC বাহুর দৈর্ঘ্য, a = √{(2+1)² + (1 − 1)2}
= √(9 +0) = 3 একক
AC বাহুর দৈর্ঘ্য, b=√{(2 − 2)² + (1 − 5)2}
= √(0 + 16) = 4 একক
s = 1/2(a+b+c) = 1/2(3 2 (3+4+5)
= 12 /2
= 6 একক
.:. ক্ষেত্রফল=√{s(s – a) (s – b) ( s – c)} বর্গ একক
= √6 (6-3) (6-4) (6 – 5) বর্গ একক
= √(6 × 3 × 2 × 1) বর্গ একক
= √(6 x 6)
= 6 বর্গ একক
চিত্র দেখে আমরা বুঝতে পারি এটি একটি সমকোণী ত্রিভুজ। পীথাগোরাসের উপপাদ্যের সাহায্যে এটি সহজেই প্রমাণ করা যায়।
AB2 = c2 = 52 = 25, BC2 = a2 = 32 = 9, CA2 = b2 = 42 = 16
BC2 + CA2 = 9 + 16 = 25 = AB2
ABC একটি সমকোণী ত্রিভুজ। AB অতিভুজ ও ∠ACB সমকোণ
উদাহরণ ৭.
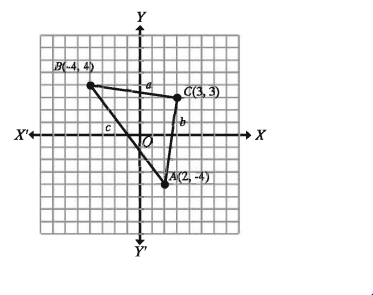
A(2, – 4), B( – 4, 4) এবং C(3,3) একটি ত্রিভুজের তিনটি শীর্ষ। ত্রিভুজটি আঁক এবং বাহুর দৈর্ঘ্য নির্ণয়ের মাধ্যমে এর ক্ষেত্রফল নির্ণয় কর। চিত্র দেখে ত্রিভুজটির একটি নাম দাও এবং এর সপক্ষে যুক্তি দেখাও ।
সমাধান:
ত্রিভুজটির চিত্র আঁকা হলো।
AB = c = √{(-4 − 2)² + (4 − (−4))2}
= √ (36 + 64)
= √100 = 10 একক
BC = a = √{3-(-4))² + (3 — 4)²}
= √49+1
= √50
= 5√2 একক
CA = b = √{(2-3)²+(-4-3)2}
= √(1 +49)
= √50
= 5√24 একক
এখন, s = 1/2(a+b+c)
= 1/2(10 + 5√2 +5√2)
= 5 + 5√2 একক
ক্ষেত্রফল =√ s (s – a) (s – b) (s – c) বর্গ একক
= √{(5 + 5√2)(5 + 5√2 – 10) (5 + 5√2 – 5√2) (5 + 5√2 – 5√2)} বর্গ একক
= (5+5√2 ) (5√2 – 5) . 5.5 বর্গ একক
= 5 √{(5+52) (5√2 – 5)} বর্গ একক
= 5 √{( 52 ) 2 – 52}
= 5√(50 – 25)
= 5√25 বর্গ একক
= 25 বর্গ একক
প্রদত্ত ত্রিভুজটি একটি সমদ্বিবাহু ত্রিভুজ। কেননা BC = CA = 5√2 একক। অর্থাৎ, ত্রিভুজটির দুইটি বাহু সমান।
আবার, AB 2 = 10² = 100
BC2 + CA2 = (5√2) 2 + (5√2 ) 2 = 50 + 50 = 100
AB2 = BC2 + CA2
.: ∆ABC একটি সমকোণী ত্রিভুজ।
অর্থাৎ ∆ABC একটি সমকোণী ও সমদ্বিবাহু ত্রিভুজ।
উদাহরণ ৮
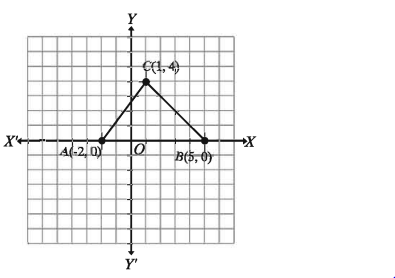
একটি ত্রিভুজের শীর্ষত্রয় যথাক্রমে A ( – 2,0 ), B (5, 0 ) এবং C(1, 4)। প্রত্যেকটি বাহুর দৈর্ঘ্য নির্ণয় কর এবং ত্রিভুজটির ক্ষেত্রফল নির্ণয় কর।
সমাধান:
ত্রিভুজটির চিত্র দেখানো হলো।
AB = c = √{(5− (−2))² + (0 – 0)²}
= √49 = 7 একক
BC= a = √{(1-5)² + (4-0)²}
= √(16+16)
= 4√2 PP
CA = b=√{(2-1)²+(0-4)2}
=√9 + 16 = 5 একক
s = 1/2 (a+b+c)
= 1/2(7+4√2+5)
= (12 + 4√2) = 6 + 2√2 একক
ক্ষেত্রফল = √s(s – a) (s—b) (s – c)
= √{(6 + 2√2) (6 + 2√2 − 7)(6 + 2√2 − 4√2)(6 +2√2 − 5)}
= √{(6 +2√√2)(2√√2 − 1)(6 − 2√2)(2√2 + 1)}
= √{ (6 + 2√2) (6 – 2√2) (2√2 + 1) (2√2 – 1) }বর্গ একক
= √{62 – (2√2) 2) ((2√2)2 – 12)}
= √28 . 7 = 14 বর্গ একক
প্রদত্ত ত্রিভুজটি একটি বিষমবাহু ত্রিভুজ। কারণ এর কোনো বাহুই অপর কোনো বাহুর সমান নয়।
লক্ষণীয়:
যে তিনটি ত্রিভুজক্ষেত্রের ক্ষেত্রফল নির্ণয় করা হলো তার ১মটি সমকোণী, ২য়টি সমদ্বিবাহু ও সমকোণী এবং তৃতীয়টি বিষমবাহু ত্রিভুজ। একটি মাত্র সূত্রের সাহায্যে প্রত্যেকটি ত্রিভুজের ক্ষেত্রফল নির্ণয় সম্ভব হয়েছে। অন্য যেকোনো ত্রিভুজের ক্ষেত্রেও ঠিক একইভাবে ক্ষেত্রফল নির্ণয় করা সম্ভব হবে। অনুশীলনীতে এ রকম আরও কয়েকটি ত্রিভুজের ক্ষেত্রফল সংক্রান্ত সমস্যা থাকবে।
উদাহরণ ৯.
একটি চতুর্ভুজের চারটি শীর্ষ যথাক্রমে A ( 1, 0 ), B (0,1), C (–1, 0) এবং D (0, − 1 ) । চতুর্ভুজটির চিত্র আঁক এবং যেকোনো দুই বাহু ও কর্ণের দৈর্ঘ্য নির্ণয়ের মাধ্যমে এর ক্ষেত্রফল নির্ণয় কর।
সমাধান:
পার্শ্বের চিত্রে বিন্দু পাতনের মাধ্যমে ABCD চতুর্ভুজটি দেখানো হলো। AB, BC, CD এবং DA চতুর্ভুজটির চারটি বাহু এবং AC ও BD চতুর্ভুজটির দুইটি কর্ণ ৷

বাহু, AB = c = √{(1-0)² + (0 −1)²} = √1 + 1 = √2
বাহু BC= a = √(0+1)² + (1 − 0)² = √1+1= √2
কর্ণ, AC = b = √(1+1)²+(0-0)² = √22 = 2 একক
বাহু, CD=√(-1 − 0)² + (0 + 1)² = √2
বাহু, DA = √(0-1)² + (−1 − 0)² = √24++ AB = BC = CD = DA = √2 একক
… চতুর্ভুজটি একটি বর্গ বা রম্বস।
AB² + BC² = (√2)² + (√2)² = 2+2 = 4 = AC2
.: চতুর্ভুজটি একটি বর্গক্ষেত্র।
চতুর্ভুজ ABCD এর ক্ষেত্রফল = 2x ত্রিভুজ ABC এর ক্ষেত্রফল
এখন ত্রিভুজ ABC এর পরিসীমা, 2s = AB + BC + CA = √2 + √2 + 2 = 2+2√2 একক
s = 1/2(2+ 2√2) = 1 + √2 একক
ত্রিভুজ ABC এর ক্ষেত্রফল = √ (s ( s – a ) ( s – b) (s – c) বর্গ একক
= √{(1 + √2)(1 + √2 – √2) (1 + √2 – 2) (1 + √2 – √2)} বর্গ একক
= √(√2 + 1) · 1 · (√2 – 1) . 1 বর্গ একক
= √(√2)2 – 1 বর্গ একক
= √2 − 1 বর্গ একক
= 1 বর্গ একক
ABCD চতুর্ভুজক্ষেত্র এর ক্ষেত্রফল = 2 × 1 বর্গ একক 2 বর্গ একক।
মন্তব্য:
বর্গের বাহুর দৈর্ঘ্যকে বর্গ করেও ক্ষেত্রফল পাওয়া যায়। আয়ত এর দৈর্ঘ্য ও প্রস্থ গুণ করেও ক্ষেত্রফল পাওয়া যায়। কিন্তু যেকোনো চতুর্ভুজের ক্ষেত্রফল নির্ণয় করা যায় না।
উদাহরণ ১০.
A (–1, 1), B(2, − 1 ), C (3,3) এবং D(1,6) দ্বারা গঠিত চতুর্ভুজটি অঙ্কন করে এর প্রতিটি বাহু ও একটি কর্ণের দৈর্ঘ্য নির্ণয় কর এবং চতুর্ভুজটির ক্ষেত্রফল নির্ণয় কর।
সমাধান:
বিন্দু পাতনের মাধ্যমে xy সমতলে ABCD চতুর্ভুজটি দেখানো হলো। ABCD চতুর্ভুজটির

বাহু AB = a = √(32 + 22) = √13 একক
বাহু BC = b = √(12 + 42) = √17 একক
বাহু CD = d = √(22 + 32) =√13 একক
বাহু DA = e = √(22 + 52) = √29 একক
কর্ণ AC = c = √(42 + 22) = √20 একক
∆ABC এ 2s = a+b+c = (√13+√17+√20) একক
= (3.6056+4.1231 + 4.4721) একক
= 12.2008 একক
s = 6.1004 একক
∆ABC এর ক্ষেত্রফল = √s ( s – a) (s – b) ( s – c) বর্গ একক –
= √(6.1004 × 2.4948 x 1.9773 x 1.6283) বর্গ একক
= 49.000 বর্গ একক = 7 বর্গ একক
∆ACD এ 2s = c + d+e = (√20 + √13 + √29) একক
= (4.4721 + 3.6056 + 5.3852) একক
= 13.4629 একক
s = 6.7315 একক।
∆ACD এর ক্ষেত্রফল = : √s ( s – c) (s – d) (s – e) বর্গ একক
= √(6.7315 × 2.2591 x 3.1256 x 1.3460) বর্গ একক
= √63.9744 বর্গ একক
= 7.9983 বর্গ একক
ABCD চতুর্ভুজ ক্ষেত্রের ক্ষেত্রফল ( 7.000 + 7.998) বর্গ একক
= 14.998 বর্গ একক 15 বর্গ একক (প্রায়)
মন্তব্য:
চতুর্ভুজটি বর্গ বা আয়ত বা সামান্তরিক বা রম্বস কোনোটিই নয়। এ ধরনের বিষম আকারের জমির ক্ষেত্রফল নির্ণয়ে এ পদ্ধতি অত্যন্ত কার্যকর।
উদাহরণ ১১
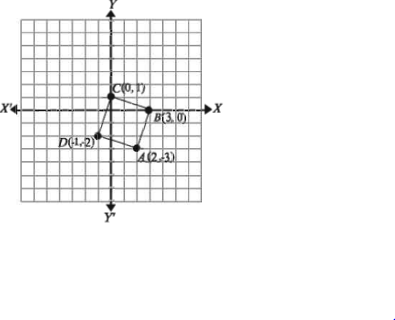
চারটি বিন্দুর স্থানাঙ্ক যথাক্রমে A (2, 3), B ( 3,0), C (0, 1) এবং D (–1, -2)।
ক) দেখাও যে, ABCD একটি রম্বস।
খ) AC ও BD এর দৈর্ঘ্য নির্ণয় কর এবং ABCD একটি বর্গ কিনা যাচাই কর।
গ) ত্রিভুজক্ষেত্রের মাধ্যমে চতুর্ভুজটির ক্ষেত্রফল নির্ণয় কর।
সমাধান:
ABCD চতুর্ভুজটি বিন্দু পাতনের মাধ্যমে দেখানো হলো।
ক) ধরি a, b, c, d যথাক্রমে AB, BC, CD এবং DA বাহুর দৈর্ঘ্য এবং কর্ণ AC = e ও কর্ণ BD = f ।
a = √{(3-2)²+(0+3)²} = √12+32 = √10 একক
b = √{(0 − 3)² + (1 − 0)²} = √32 +12= √10 একক
c = √{(−1 – 0)2 + (- 2 – 1)2} = √12 + 32 = √10 একক
d = √{(2+1)2 + (−3+ 2)²} = √32+12 = √10 একক
যেহেতু a = b = c = d = √10 একক
.:. ABCD একটি রম্বস ।
খ) কর্ণ AC = e = √{(0 – 2)2 + ( 1 + 3)2} = √4 + 16 = √20 একক
এবং কর্ণ BD = f = √[(−1 – 3)2 + (− 2 – 0)2} = √42 + 22 = √20 একক
দেখা যাচ্ছে AC = BD অর্থাৎ, কর্ণদ্বয় সমান
AC2 = (√20)2 = 20
AB2 + BC2 = (√10)2 + (V10) 2 = 10 + 10 = 20 = AC2
পীথাগোরাসের উপপাদ্য অনুযায়ী ZABC সমকোণ।
ABCD চতুর্ভুজটি একটি বর্গ।
গ) চতুর্ভুজ ABCD এর ক্ষেত্রফল =2 x ত্রিভুজ ABC এর ক্ষেত্রফল
এখানে ∆ABC এর ক্ষেত্রে
s = 1/2(a + b + c) = (√10+ √10+ √20)/2 = (2√10+2√5) /2 = √10+ √5
∆ABC এর ক্ষেত্রফল
= √s ( s – a) (s – b) (s – e) বর্গ একক
= √(√10+ √5)(√/10 + √5 − √/10)(√/10+ √5 − √/10)(√/10 + √5 − √20) বর্গ একক
= √(√10 + √5) . √5 . √5 . (√10 – 5) বর্গ একক .
√{5. ((V10) 2 – (√5) 2)}
= √5 . 5 = 5 বর্গ একক
ABCD বর্গের ক্ষেত্রফল = = 2 × 5 বর্গ একক = 10 বর্গ একক।
মন্তব্য:
সহজ পদ্ধতি ABCD বর্গটির ক্ষেত্রফল = (√10) 2 = 10 বর্গ একক।
পদ্ধতি ২: শীর্ষবিন্দুর স্থানাঙ্কের সাহায্যে ক্ষেত্রফল নির্ণয়
এই পদ্ধতিতে একটি ত্রিভুজের তিনটি শীর্ষবিন্দুর স্থানাঙ্কের সাহায্যে খুব সহজেই ত্রিভুজক্ষেত্রের ক্ষেত্রফল নির্ণয় করা যায়। একইভাবে যেকোনো বহুভুজের শীর্ষবিন্দুর স্থানাঙ্ক জানা থাকলেও বহুভুজের ক্ষেত্রফল নির্ণয় সম্ভব। বাস্তব ক্ষেত্রে এই পদ্ধতি ব্যবহার করা সম্ভব হয় না। এর কারণ হলো আমরা যদি একটি জমির ক্ষেত্রফল নির্ণয় করতে চাই এবং জমিটি যদি ত্রিকোণাকার বা চৌকোণাকার হয় তাহলে এই পদ্ধতিতে ক্ষেত্রফল নির্ণয় করা যাবে না। যেহেতু কৌণিক বিন্দুসমূহের স্থানাঙ্ক আমাদের জানা নাই বা জানা সম্ভব নয়। কিন্তু জমিটির বাহুর দৈর্ঘ্য আমরা সহজেই মেপে নিতে পারি এবং ১ নং পদ্ধতিতে ক্ষেত্রফল নির্ণয় করতে পারি। তাই উভয় পদ্ধতি সম্পর্কে শিক্ষার্থীদের ধারণা থাকা প্রয়োজন। ২ নং পদ্ধতির সাহায্যে ত্রিভুজ ও বহুভুজের ক্ষেত্রফল নির্ণয়ের কৌশল উদাহরণের সাহায্যে ব্যাখ্যা করা হলো:
ত্রিভুজক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সাধারণ সূত্র:
ধরি, A (x1,y1), B(x2, Y2) এবং C(x3, Y3) ত্রিভুজ ABC এর তিনটি শীর্ষবিন্দু। নিচের চিত্রের অনুরূপ A, B ও C বিন্দু ঘড়ির কাঁটার বিপরীত দিকে সাজানো।

বহুভুজ ABCDF এর ক্ষেত্রফল = ত্রিভুজক্ষেত্র ABC এর ক্ষেত্রফল + ট্রাপিজিয়ামক্ষেত্র ACDF এর ক্ষেত্রফল।
= ট্রাপিজিয়ামক্ষেত্র ABEF এর ক্ষেত্রফল + ট্রাপিজিয়ামক্ষেত্র BCDE এর ক্ষেত্রফল।
সুতরাং আমরা পাই,
ত্রিভুজক্ষেত্র ABC এর ক্ষেত্রফল = ট্রাপিজিয়ামক্ষেত্র ABEF এর ক্ষেত্রফল + ট্রাপিজিয়ামক্ষেত্র BCDE এর ক্ষেত্রফল – ট্রাপিজিয়ামক্ষেত্র ACDF এর ক্ষেত্রফল ।
ত্রিভুজক্ষেত্র ABC এর ক্ষেত্রফল
= 1/2 × (BE+AF) × EF + 1/2 × (CD+BE) × DE – 1/2 × (CD + AF) × DF
= 1/2 × (Y2 + Y1) × (x1 − x2) + 1/2 × (Y3 + Y2) × (x2 − x3) − 1/2 × (Y3 +31) × (X1 − X3)
= 1/2 (X1Y2+ X2Y3+ X3Y1-X2Y1 – X3Y2 – X1Y3) বর্গ একক
যেখানে গুণফলের দিক ধনাত্মক চিহ্ন হিসেবে নিয়ে পাওয়া গেছে 12 + 2Y3 + 3y1 এবং গুণফলের দিক ঋণাত্মক চিহ্ন হিসেবে নিয়ে পাওয়া গেছে – x2y2 -X3Y2 – X1Y3 .
উদাহরণ ১২.
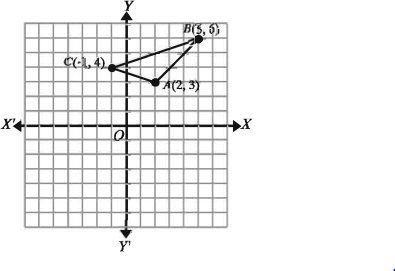
A (2, 3), B(5, 6) এবং C (–1, 4) শীর্ষবিশিষ্ট ABC ত্রিভুজের ক্ষেত্রফল নির্ণয় কর।
সমাধান:
A (2, 3), B(5, 6) এবং C (–1, 4) শীর্ষ তিনটিকে ঘড়ির কাঁটার বিপরীত দিকে নেওয়া হলো ।
∆ABC এর ক্ষেত্রফল
= 1 /2 ∣ 2 5 -1 2 ∣ বৰ্গ একক
∣ 3 6 4 3 ∣
= 1/2 ( 12 + 20 – 3 – 15 + 6 – 8) বর্গ একক
= 1/2 (12) বর্গ একক
= 6 বর্গ একক
উদাহরণ ১৩.
একটি ত্রিভুজের তিনটি শীর্ষ A (1, 3), B( 5, 1 ) এবং C (3, r) এর ক্ষেত্রফল 4 বর্গ একক হলে । এর সম্ভাব্য মানসমূহ নির্ণয় কর।
সমাধান :
A (1, 3), B( 5, 1 ) এবং C (3, r) শীর্ষ তিনটি ঘড়ির কাঁটার বিপরীত দিকে বিবেচনা করে ∆ABC এর ক্ষেত্রফল
= 1/2 ∣ 1 5 3 1 ∣ বর্গ একক
∣ 3 1 r 3 ∣
= ½ (1 + 5r + 9 – 15 – 3 – 1) বর্গ একক
= 1/2(4r – 8) = (2r – 4) বর্গ একক
প্রশ্নমতে, |(2r – 4)| = 4
বা, ±(2r – 4) = 4
বা, 2r – 4 = ±4
অর্থাৎ, 2r = 0 বা, ৪
r = 0, 4

৩ thoughts on “ত্রিভুজক্ষেত্রের ক্ষেত্রফল”