আজকে আমরা আলোচনা করবো গণিতের ফাংশন সম্পর্কে । যা উচ্চতর গণিতের সেট ও ফাংশন অংশের অন্তর্গত।
গণিতের ফাংশন
সেটের মতো ফাংশনের ধারণাও গণিতে একটি অত্যন্ত গুরুত্বপূর্ণ বিষয়। ব্যবহারিক প্রয়োজনে দুইটি চলক অথবা দুইটি সেটের মধ্যে সম্পর্ক বিবেচনা করা হয়।
উদাহরণ ২০.
বৃত্তের ব্যাসার্ধ ও পরিসীমার মধ্যে যে সম্পর্ক তাকে p = – 2nr লিখে প্রকাশ করা হয় যেখানে ” চলক বৃত্তের ব্যাসার্ধ ও p চলক বৃত্তের পরিসীমা নির্দেশ করে। এখানে । এর প্রত্যেক সম্ভাব্য মানের জন্য p এর একটি ও কেবল একটি মান নির্দিষ্ট হয়। আমরা বলি, p চলক r চলকের একটি ফাংশন এবং লিখি p = f(r), যেখানে f(r) = 2nr ।
এই ফাংশনীয় সম্পর্কটি দ্বারা r এর ব্যাপ্তি সেট X থেকে p এর ব্যাপ্তি সেট Y এ একটি ফাংশন সংজ্ঞায়িত হয়েছে বলেও ধরা হয়। এই ফাংশনকে X থেকে Y তে বর্ণিত অন্বয় {(r,p) : r ∈ X এবং p ∈ Y ও p = 2nr} রূপেও বিবেচনা করা হয়। অন্বয়ের ধারণা নবম-দশম শ্রেণির গণিত বইএ ব্যাখ্যা করা হয়েছে।

সংজ্ঞা ৫ (ফাংশন)
যদি X ও Y সেট হয় এবং কোনো নিয়মের অধীনে X সেটের প্রত্যেক উপাদানের সঙ্গে Y সেটের একটি ও কেবল একটি উপাদানকে সংশ্লিষ্ট করা হয় তবে ঐ নিয়মকে X থেকে Y এ বর্ণিত একটি ফাংশন বলা হয়। এরূপ ফাংশনকে f, g, F, G ইত্যাদি প্রতীক দ্বারা নির্দেশ করা হয়।
সংজ্ঞা ৬ (ডোমেন ও কোডোমেন)
যদি X সেট হতে Y সেটে f একটি ফাংশন হয়, তবে তাকে f : X → Y লিখে প্রকাশ করা হয়। X সেটকে f : X + Y ফাংশনের ডোমেন (domain) এবং Y সেটকে এর কোডোমেন (codomain) বলা হয়।
সংজ্ঞা ৭ (প্রতিবিম্ব ও প্রাক প্রতিবিম্ব).
যদি f : X → Y ফাংশনের অধীনে x ∈ X এর সাথে y ∈ Y সংশ্লিষ্ট হয়, তবে এই ফাংশনের অধীনে y কে এর প্রতিবিম্ব বা ইমেজ (image) এবং x কে y এর প্রাক প্রতিবিম্ব (preimage) বলা হয় এবং y = f(x) লিখে তা প্রকাশ করা হয়।
সংজ্ঞা ৮ (রেঞ্জ).
f : x + y ফাংশনের অধীনে Y এর যে সকল উপাদান X এর কোনো উপাদানের ইমেজ হয়, এদের সেটকে f ফাংশনের রেঞ্জ (range) বলা হয় এবং “রেঞ্জ f” দ্বারা প্রকাশ করা হয়। অর্থাৎ রেঞ্জ f = {y : y = f(x) যেখানে x ∈ X} = {f(x) : x ∈ X}। লক্ষণীয় যে রেঞ্জ f কোডোমেন Y এর উপসেট।
ফাংশনকে বিভিন্নভাবে বর্ণনা করা যায়। নিচের উদাহরণগুলো লক্ষ কর।

উদাহরণ ২১.
f : x → 2x + 1, x ∈ Z; পূর্ণ সংখ্যার সেট Z হতে z এ একটি ফাংশন বর্ণনা করে। এই ফাংশনের অধীনে পূর্ণসংখ্যা x এর প্রতিবিম্ব y = f(x) = 2x + 1; ফাংশনটির ডোমেন, ডোম f = Z এবং ফাংশনটির রেঞ্জ, রেঞ্জ f {y: y = 2x + 1, x ∈ Z} সকল বিজোড় পূর্ণসংখ্যার সেট।
উদাহরণ ২২.
ক্রমজোড়ের সেট F = { (0, 0), (1, 1), (–1, 1), (2, 4), (2, 4), ( 3, 9), (-3, 9) } একটি ফাংশন বর্ণনা করে, যার ডোমেন হলো F এর অন্তর্ভুক্ত ক্রমজোড়গুলোর প্রথম অংশকগুলোর সেট এবং রেঞ্জ হলো F এর অন্তর্ভুক্ত ক্রমজোড়গুলোর দ্বিতীয় অংশকগুলোর সেট।
অর্থাৎ ডোম F = {0, 1, – 1, 2, – 2, 3, – 3} এবং রেঞ্জ F = {0, 1, 4, 9}
একটু লক্ষ করলে এক্ষেত্রে দেখা যাবে যে F এর অধীনে x ∈ ডোম F এর প্রতিবিম্ব F(x) = x2 উল্লেখ্য যে, একটি ক্রমজোড়ের সেট কেবল তখনই একটি ফাংশন বর্ণনা করে যখন ভিন্ন ভিন্ন ক্রমজোড়ের প্রথম অংশক ভিন্ন হয়।
উদাহরণ ২৩
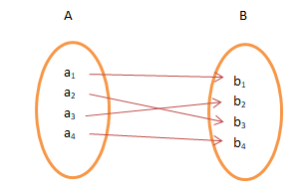
নিচে বর্ণিত ফাংশন F এর ডোমেনকে A ও রেঞ্জকে B ধরে ফাংশনটিকে চিত্র দ্বারা বর্ণনা করা যায়, যেখানে A এর প্রত্যেক বিন্দু থেকে একটি ও কেবল একটি তীর চিহ্নিত রেখা আরম্ভ হয়ে B সেটের একটি ও কেবল একটি বিন্দুতে শেষ হয়েছে (বামের চিত্র)। উল্লেখ্য যে, ফাংশনের কোডোমেন হিসেবে একটি সেট Y (যার উপসেট B) নিয়েও ফাংশনটিকে চিত্রিত করা যায় (ডানের চিত্র)।
ফাংশন: মান নির্ণয় :
