আজকে আমাদের আলোচনার বিষয়ঃ গণিতে অন্বয়। এটি নবম – দশম শ্রেনী গণিতের সেট ও ফাংশন এর অন্তর্গত।

গণিতে অন্বয়
আমরা জানি, বাংলাদেশের রাজধানী ঢাকা, ভারতের রাজধানী নতুন দিল্লী এবং থাইল্যান্ডের রাজধানী ব্যাংকক। এখানে দেশের সাথে রাজধানীর একটি অন্বয় বা সম্পর্ক আছে। এ সম্পর্ক হচ্ছে দেশ-রাজধানী অন্বয়। উক্ত সম্পর্ককে সেট আকারে নিম্নরূপে দেখানো যায় :
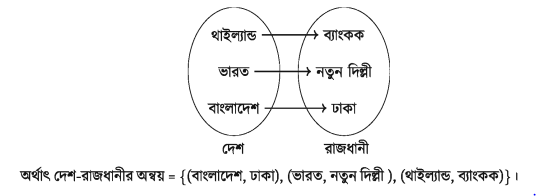
যদি A ও B দুইটি সেট হয় তবে সেটদ্বয়ের কার্তেসীয় গুণজ Ax B সেটের অন্তর্গত ক্রমজোড়গুলোর অশূন্য উপসেট R কে A সেট হতে B সেটের একটি অন্বয় বা সম্পর্ক বলা হয়। এখানে, R সেট AX B সেটের একটি উপসেট অর্থাৎ, R⊆ Ax B
উদাহরণ ১৫.
মনে করি, A = { 3,5} এবং B = {2, 4}
A x B = {3,5} × {2, 4} = {(3,2), (3, 4), (5, 2), (5,4)}
R⊆ {(3,2), (3,4), (5, 2), (5, 4)}
যখন A সেটের একটি উপাদান ও B সেটের একটি উপাদান এবং (x, y) ∈ R হয় তবে লেখা হয় x R y এবং পড়া হয় x, y এর সাথে অন্বিত (r is related to y) অর্থাৎ উপাদান উপাদান I, y এর সাথে R সম্পর্কযুক্ত।
যদি x > y শর্ত হয় তবে, R = { (3, 2), ( 5, 2 ), ( 5, 4)}
এবং যদি x < y শর্ত হয় তবে, R = { ( 3, 4) }
আবার, A সেট হতে A সেটের একটি অন্বয় অর্থাৎ RCAX A হলে, R কে A এর অন্বয় বলা হয়।
A এবং B দুইটি সেটের উপাদানগুলোর মধ্যে সম্পর্ক দেওয়া থাকলে x ∈ A এর সংগে সম্পর্কিত y ∈ B নিয়ে যে সব ক্রমজোড় (x, y) পাওয়া যায়, এদের অশূন্য উপসেট হচ্ছে একটি অন্বয়।
উদাহরণ ১৬.
যদি P = {2, 3, 4}, Q = {4, 6} এবং P ও Q এর উপাদানগুলোর মধ্যে y : = সম্পর্ক বিবেচনায় থাকে তবে সংশ্লিষ্ট অন্বয় নির্ণয় কর।
সমাধান:
দেওয়া আছে, P = {2, 3, 4} এবং Q = { 4, 6}
প্রশ্নানুসারে, R = {(x, y) : x ∈ P, y Q এবং y = 2x}
এখানে, P × Q = {2, 3, 4} x {4, 6} = {(2, 4), (2, 6), ( 3, 4), ( 3, 6 ), ( 4, 4), ( 4, 6 ) }
R = {(2, 4), ( 3, 6) }
নির্ণেয় অন্বয় {(2, 4), ( 3, 6) }
উদাহরণ ১৭.
যদি A = {1, 2, 3}, B = {0, 2, 4} এবং A ও B এর উপাদানগুলোর মধ্যে x = y − 1 সম্পর্ক বিবেচনায় থাকে, তবে সংশ্লিষ্ট অন্বয় বর্ণনা কর।
সমাধান:
দেওয়া আছে, A = {1, 2, 3}, B = {0, 2, 4}
প্রশ্নানসারে, অন্বয় R = {(x, y) : x ∈ A, y ∈ B এবং x = y − 1}
এখানে, A × B = {1, 2, 3} x {0, 2, 4}
= {(1, 0), (1, 2), (1, 4), (2, 0), (2, 2), (2, 4), (3, 0), (3, 2), (3, 4)}
R = {(1, 2),(3, 4)}
