গণিতে ক্রমজোড়

আজকে আমাদের আলোচনার বিষয়ঃ গণিতে ক্রমজোড় । এটি নবম – দশম শ্রেনী গণিতের সেট ও ফাংশন এর অন্তর্গত।

 

 

গণিতে ক্রমজোড়

অষ্টম শ্রেণির আমেনা এবং সুমেনা বার্ষিক পরীক্ষায় মেধা তালিকায় যথাক্রমে প্রথম ও দ্বিতীয় হলো । মেধা অনুসারে তাদেরকে (আমেনা, সুমেনা) জোড়া আকারে লেখা যায়। এরূপ নির্দিষ্ট করে দেওয়া জোড়াকে একটি ক্রমজোড় বলে।

সুতরাং, একজোড়া উপাদানের মধ্যে কোনটি প্রথম অবস্থানে আর কোনটি দ্বিতীয় অবস্থানে থাকবে, তা নির্দিষ্ট করে জোড়া আকারে প্রকাশকে ক্রমজোড় বলা হয়।

যদি কোনো ক্রমজোড়ের প্রথম উপাদান বা পদ x এবং দ্বিতীয় উপাদান বা পদ y হয়, তবে ক্রমজোড়টিকে (x, y) দিয়ে প্রকাশ করা হয়। ক্রমজোড় (x, y) ও (a,b) সমান বা (x, y) = (a,b) হবে যদি x = a এবং y = b হয়।

 

 

উদাহরণ ১১.

(2x + y 3 ) = (6, x – y) হলে (x,y) নির্ণয় কর।

সমাধান:

দেওয়া আছে, ( 2x + y 3 ) = (6x – 1 )

ক্রমজোড়ের শর্তমতে,

2x + y = 6 …… (1)

x – y = 3 ….. (2)

সমীকরণ (1) ও (2) যোগ করে পাই, 3x = 9 বা x =3

সমীকরণ (1) এ x এর মান বসিয়ে পাই, 6 + y = 6 বা y = 0

(x, y) = (3,0)

 

 

কার্তেসীয় গুণজ (Cartesian Product )

করিম সাহেব তাঁর বাড়ির একটি ঘরের ভিতরের দেওয়ালে সাদা বা নীল রং এবং বাইরের দেওয়ালে লাল বা হলুদ বা সবুজ রং এর লেপন দেওয়ার সিদ্ধান্ত নিলেন। ভিতরের দেওয়ালে রং এর সেট A {সাদা, নীল} এবং বাইরের দেওয়ালে রং এর সেট B {লাল, হলুদ ও সবুজ}। করিম সাহেব তাঁর ঘরের রং লেপন (সাদা, লাল), (সাদা, হলুদ), (সাদা, সবুজ), (নীল, লাল), (নীল, হলুদ), (নীল, সবুজ) ক্রমজোড় আকারে দিতে পারেন।

উক্ত ক্রমজোড়ের সেটকে নিচের মতো করে লেখা হয়:

Ax B = {(সাদা, লাল), (সাদা, হলুদ), (সাদা, সবুজ), (নীল, লাল), (নীল, হলুদ), (নীল, সবুজ)}

উপরোক্ত ক্রমজোড়ের সেটটিকেই কার্তেসীয় গুণজ সেট বলা হয়।

সেট গঠন পদ্ধতিতে, Ax B = {(x, y) : x ∈ A এবং y ∈ B }

A × B কে পড়া হয় A ক্রস B।

উদাহরণ ১২.

P = {1, 2, 3}, Q = {3, 4}, R = P⋂ Q হলে P x R এবং R x Q নির্ণয় কর।

সমাধান:

দেওয়া আছে, P = {1, 2, 3}, Q = { 3, 4}

এবং R = P⋂Q = {1, 2, 3} { 3, 4} = {3}

P × R = {1, 2, 3} x {3} = { (1, 3), (2, 3), (3, 3)}

এবং R × Q = {3} x { 3, 4} = { (3, 3), ( 3, 4)}

 

 

উদাহরণ ১৩.

যে সকল স্বাভাবিক সংখ্যা দ্বারা 311 এবং 419 কে ভাগ করলে প্রতি ক্ষেত্রে 23 অবশিষ্ট থাকে এদের সেট নির্ণয় কর।

সমাধান:

যে স্বাভাবিক সংখ্যা দ্বারা 311 এবং 419 কে ভাগ করলে প্রতিক্ষেত্রে 23 অবশিষ্ট থাকে, সে সংখ্যা হবে 23 অপেক্ষা বড় এবং 311 – 23 = 288 এবং 419 – 23 = 396 এর সাধারণ গুণনীয়ক।

মনে করি, 23 অপেক্ষা বড় 288 এর গুণনীয়কসমূহের সেট A।

এখানে, 288 = 1 x 288 = 2 x 144 = 3 x 96 = 4 x 72 = 6 x 48 = 8 x 36 = 9 x 32 = 12 x 24 = 16 x 18

A= {24, 32, 36, 48, 72, 96, 144, 288}

মনে করি, 23 অপেক্ষা বড় 396 এর গুণনীয়কসমূহের সেট B

এখানে, 396 = 1 x 396 = 2 x 198 = 3 x 132 = 4 x 99 = 6 x 66 = 9 x 44 = 11 × 36 = 12 x 33 = 18 x 22

B = {33, 36, 44, 66, 99, 132, 198, 396)

A⋂B = {24, 32, 36, 48, 72, 96, 144, 288} {33, 36, 44, 66, 99, 132, 198, 396)

A⋂B = { 36}

নির্ণেয় সেট {36}

উদাহরণ ১৪.

100 জন শিক্ষার্থীর মধ্যে কোনো পরীক্ষায় ৪৪ জন বাংলায়, 80 জন গণিতে এবং 70 জন উভয় বিষয়ে পাশ করেছে। ভেনচিত্রের সাহায্যে তথ্যগুলো প্রকাশ কর এবং কতজন শিক্ষার্থী উভয় বিষয়ে ফেল করেছে, তা নির্ণয় কর।

 

 

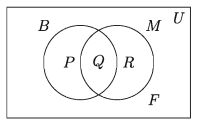
সমাধান:

ভেনচিত্রে আয়তাকার ক্ষেত্রটি 100 জন শিক্ষার্থীর সেট U এবং বাংলায় ও গণিতে পাশ শিক্ষার্থীদের সেট যথাক্রমে B ও M দ্বারা নির্দেশ করে। ফলে ভেনচিত্রটি চারটি নিশ্ছেদ সেটে বিভক্ত হয়েছে, যাদেরকে P, Q, R, F দ্বারা চিহ্নিত করা হলো।

এখানে, উভয় বিষয়ে পাশ শিক্ষার্থীদের সেট Q = B⋂M, যার সদস্য সংখ্যা 70

P = শুধু বাংলায় পাশ শিক্ষার্থীদের সেট, যার সদস্য সংখ্যা = 88 70 = 18

R = শুধু গণিতে পাশ শিক্ষার্থীদের সেট, যার সদস্য সংখ্যা = 80-70 = 10

P⋃Q⋃R = B⋃M, যেকোনো একটি বিষয়ে এবং উভয় বিষয়ে পাশ শিক্ষার্থীদের সেট, যার সদস্য সংখ্যা = 18 + 10 + 70 = 98

F = উভয় বিষয়ে ফেল করা শিক্ষার্থীদের সেট, যার সদস্য সংখ্যা = 100 – 98 = 2

উভয় বিষয়ে ফেল করেছে 2 জন শিক্ষার্থী।