আজকে আমাদের আলোচনার বিষয়ঃ গণিতে ফাংশন। এটি নবম – দশম শ্রেনী গণিতের সেট ও ফাংশন এর অন্তর্গত।
গণিতে ফাংশন
ফাংশন হচ্ছে বিশেষ ধরনের অন্বয় । X ও Y দুইটি সেট, X সেটের প্রতি‘টি সদস্য, Y সেটের একটি‘ মাত্র সদস্যে‘র সাথে সম্পর্কি‘ত হলে, এ সম্পর্ককে ফাংশন (function) বলে। ফাংশন‘কে সাধারণ‘ত ইংরেজি ছো‘ট হাতে‘র অক্ষ‘রে (f, g, h ) প্রকা‘শ ক‘রা হয়।
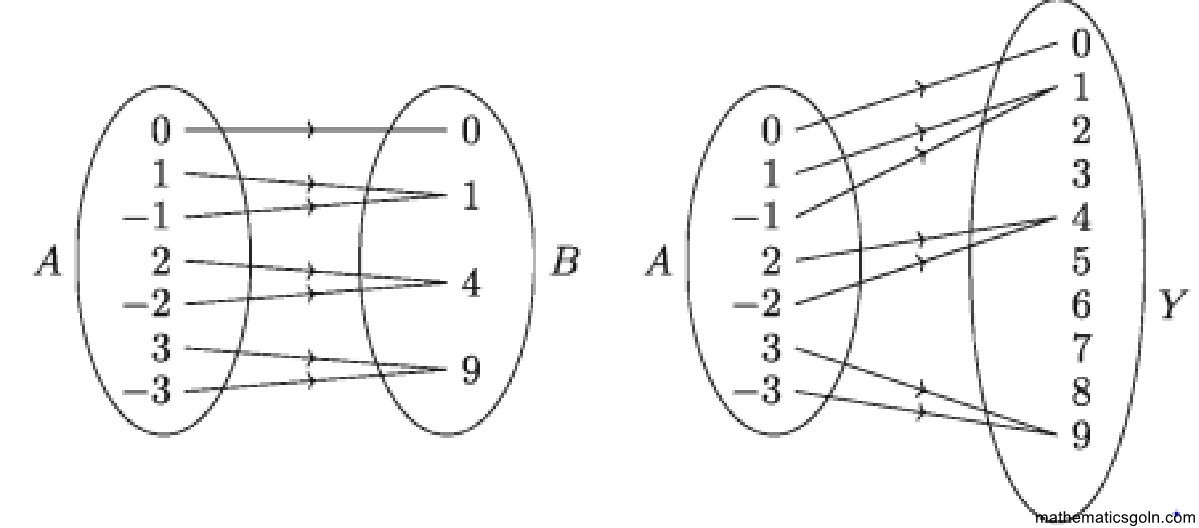
নিচের A ও B সেটের অন্বয় লক্ষ করি:
যখন y = x + 2, তখন
x = 1 হলে, y = 3
x = 2 হলে, y = 4
x = 3 হলে, y = 5
অর্থাৎ x এর একটি মানের জন্য y এর মাত্র একটি মান পাওয়া যায় এবং x ও y-এর মধ্যে সম্পর্ক তৈরি হয় y = x + 2 দ্বারা। সুতরাং দুইটি চলক x এবং y এমনভাবে সম্পর্কযুক্ত যেন এর যেকোনো একটি মানের জন্য y এর একটি মাত্র মান পাওয়া যায়, তবে y কে x এর ফাংশন বলা হয়। এর ফাংশনকে সাধারণত y, f(x), g (x), F(x) ইত্যাদি দ্বারা প্রকাশ করা হয় ।

মনে করি, y = x2 – 2x + 3 একটি ফাংশন। এখানে, x এর যে কোনো একটি মানের জন্য এর y একটি মাত্র মান পাওয়া যাবে। এখানে, x এবং y উভয়ই চলক তবে, x এর মানের উপর y এর মান নির্ভরশীল। কাজেই হচ্ছে স্বাধীন চলক এবং y হচ্ছে অধীন চলক।
উদাহরণ ১৮.
f(x) = x2 – 4x + 3 হলে, f(−1) নির্ণয় কর।
সমাধান:
দেওয়া আছে, f(x) = x2 – 4x + 3
f(-1)=(-1)² – 4(-1)+31 +4+3=8

উদাহরণ ১৯.
যদি g(x) = x3 + ax2 – 3x – 6 হয়, তবে a এর কোন মানের জন্য g(-2) = 0?
সমাধান:
দেওয়া আছে, g (x) = x3 + ax2 – 3x – 6
g(-2) = (-2)3 + a(-2)² -3(-2) – 6
= 8 + 4a +6 – 6 = 4a – 8
প্রশ্নানুসারে g(-2) = 0
4a – 8 = 0 বা, 4a = 8 বা, a = 2
a = 2 হলে, g (-2) = 0 হবে।
