আজকে আমাদের আলোচনার বিষয়ঃ গণিতে সেট। এটি নবম – দশম শ্রেনী গণিতের সেট ও ফাংশন এর অন্তর্গত।

গণিতে সেট
বাস্তব বা চিন্তা জগতের সু-সংজ্ঞায়িত বস্তুর সমাবেশ বা সংগ্রহকে সেট বলে। যেমন, নবম-দশম শ্রেণির বাংলা, ইংরেজি ও গণিত বিষয়ে তিনটি পাঠ্য বইয়ের সেট। প্রথম দশটি বিজোড় স্বাভাবিক সংখ্যার সেট, পূর্ণসংখ্যার সেট, বাস্তব সংখ্যার সেট ইত্যাদি। সেটকে সাধারণত ইংরেজি বর্ণমালার বড় হাতের অক্ষর A, B, C, … X, Y, Z দ্বারা প্রকাশ করা হয়।
যেমন, 2, 4, 6 সংখ্যা তিনটির সেট A = {2, 4, 6}
সেটের প্রত্যেক বস্তু বা সদস্যকে সেটের উপাদান (element) বলা হয়। যেমন, B = {a, b} হলে, B সেটের উপাদান a এবং b; উপাদান প্রকাশের চিহ্ন ∈ ।
a ∈ B এবং পড়া হয় a, B এর সদস্য (a belongs to B)
b∈ B এবং পড়া হয় b, B এর সদস্য (b belongs to B)
উপরের B সেটে উপাদান নেই।
C ∉ B এবং পড়া হয় c, B এর সদস্য নয় (c does not belong to B) |
সেট প্রকাশের পদ্ধতি
সেটকে দুই পদ্ধতিতে প্রকাশ করা হয়। যথা: তালিকা পদ্ধতি (Roster Method বা Tabular Method) ও সেট গঠন পদ্ধতি (Set Builder Method) ।
তালিকা পদ্ধতি:
এ পদ্ধতিতে সেটের সকল উপাদান সুনির্দিষ্টভাবে উল্লেখ করে দ্বিতীয় বন্ধনী {} এর মধ্যে আবদ্ধ করা হয় এবং একাধিক উপাদান থাকলে ‘কমা’ ব্যবহার করে উপাদানগুলোকে আলাদা করা হয়। যেমন, A = {a, b}, B = {2, 4, 6}, C = {নিলয়, তিশা, শুভ্রা} ইত্যাদি।
সেট গঠন পদ্ধতি :
এ পদ্ধতিতে সেটের সকল উপাদান সুনির্দিষ্টভাবে উল্লেখ না করে উপাদান নির্ধারণের জন্য সাধারণ ধর্মের উল্লেখ থাকে। যেমন: A {x : x স্বাভাবিক বিজোড় সংখ্যা }, B = {x : = নবম শ্রেণির প্রথম পাঁচজন শিক্ষার্থী} ইত্যাদি। এখানে, ‘: দ্বারা ‘এরূপ যেন’ বা সংক্ষেপে ‘যেন’ (such that) বোঝায়। যেহেতু এ পদ্ধতিতে সেটের উপাদান নির্ধারণের জন্য শর্ত বা নিয়ম (Rule) দেওয়া থাকে, এ জন্য এ পদ্ধতিকে Rule Method ও বলা হয়।

উদাহরণ ১.
A = { 7, 14, 21, 28 } সেটটিকে সেট গঠন পদ্ধতিতে প্রকাশ কর।
সমাধান:
A সেটের উপাদানসমূহ 7, 14, 21, 28
এখানে, প্রত্যেকটি উপাদান 7 দ্বারা বিভাজ্য, অর্থাৎ 7 এর গুণিতক এবং 28 এর বড় নয়।
A = {x : x, 7 এর গুণিতক এবং 0 < x < 28}
উদাহরণ ২.
B = {x : x, 28 এর গুণনীয়ক} সেটটিকে তালিকা পদ্ধতিতে প্রকাশ কর।
সমাধান:
এখানে, 28 = 1 x 28 = 2 × 14 = 4 × 7
28 এর গুণনীয়কসমূহ 1, 2, 4, 7, 14, 28
নির্ণেয় সেট B = {1, 2, 4, 7, 14, 28
উদাহরণ ৩.
C = {x : x ধনাত্মক পূর্ণসংখ্যা এবং x2 < 18} সেটটিকে তালিকা পদ্ধতিতে প্রকাশ কর।
সমাধান:
ধনাত্মক পূর্ণসংখ্যাসমূহ 1, 2, 3, 4, 5, …
এখানে,
x = 1 হলে, x2 = 12 = 1; x = 2 হলে, x 2 = 22 = 4
x = 3 হলে, x2 = 32 = 9; x = 4 হলে, x 2 = 42 = 16
x = 5 হলে, x2 = 52 = 25; যা 18 এর চেয়ে বড়।
.:. শর্তানুসারে গ্রহণযোগ্য ধনাত্মক পূর্ণসংখ্যাসমূহ 1, 2, 3 এবং 4
.:. নির্ণেয় সেট C = {1, 2, 3, 4}
সসীম সেট (Finite Set)
যে সেটের উপাদান সংখ্যা গণনা করে নির্ধারণ করা যায়, তাকে সসীম সেট বলে। যেমন, D = {x, y, 2}, E = {3, 6, 9, 60}, F = {x : x মৌলিক সংখ্যা এবং 30 < < 70} ইত্যাদি সসীম সেট। এখানে, D সেটে 3 টি E সেটে 20 টি এবং F সেটে 9 টি উপাদান আছে।
অসীম সেট (Infinite Set)
যে সেটের উপাদান সংখ্যা গণনা করে শেষ করা যায় না, তাকে অসীম সেট বলে। যেমন, A = {x : x বিজোড় স্বাভাবিক সংখ্যা}, স্বাভাবিক সংখ্যার সেট N = {1, 2, 3, 4, …}, পূর্ণসংখ্যার সেট Z = {…, −3, −2, -1,0,1,2,3…}, মূলদ সংখ্যার সেট Q = { : a ও b পূর্ণসংখ্যা এবং b≠ 0}, বাস্তব সংখ্যার সেট R ইত্যাদি অসীম সেট।

উদাহরণ ৪.
দেখাও যে, সকল স্বাভাবিক সংখ্যার সেট একটি অসীম সেট।
সমাধান:
স্বাভাবিক সংখ্যার সেট N = {1, 2, 3, 4, 5, 6, 7, 8, }
N সেট থেকে বিজোড় স্বাভাবিক সংখ্যাসমূহ নিয়ে গঠিত সেট A = {1, 3, 5, 7,
N সেট থেকে জোড় স্বাভাবিক সংখ্যাসমূহ নিয়ে গঠিত সেট B = {2,4,6,8,…}
N সেট থেকে 3 এর গুণিতকসমূহের সেট C = {3, 6, 9, 12, …} ইত্যাদি।
এখানে, N সেট থেকে গঠিত উপরের সেটসমূহের উপাদান সংখ্যা গণনা করে নির্ধারণ করা যায় না। ফলে A, B, C অসীম সেট।
… N একটি অসীম সেট।
ফাঁকা সেট (Empty Set)
যে সেটের কোনো উপাদান নেই তাকে ফাঁকা সেট বলে। ফাঁকা সেটকে দ্বারা প্রকাশ করা হয়। যেমন: একটি বালিকা বিদ্যালয়ের তিনজন ছাত্রের সেট, {x ∈N : 10 < < 11}, { ∈ N : x মৌলিক সংখ্যা এবং 23 < x < 29} ইত্যাদি।
ভেনচিত্র (Venn Diagram)
জন ভেন (১৮৩৪-১৯২৩) সেটের কার্যবিধি চিত্রের সাহায্যে প্রকাশ করেন। এতে বিবেচনাধীন সেটগুলোকে সমতলে অবস্থিত বিভিন্ন আকারের জ্যামিতিক চিত্র যেমন আয়ত, বৃত্ত এবং ত্রিভুজ ব্যবহার করা হয়। জন ভেনের নামানুসারে চিত্রগুলো ভেন চিত্র নামে পরিচিত।
উপসেট (Subset)
A {a,b} একটি সেট। এই সেটের উপাদান থেকে {a, b}, {a}, {6} সেটগুলো গঠন করা = যায়। আবার, কোনো উপাদান না নিয়ে Ø সেট গঠন কর যায়। এখানে, গঠিত {a, b}, {a}, {b}, Ø প্রত্যেকটি A সেটের উপসেট। সুতরাং কোনো সেট থেকে যতগুলো সেট গঠন করা যায়, এদের প্রত্যেকটি সেটকে ঐ সেটের উপসেট বলা হয়। উপসেটের চিহ্ন C। যদি B সেট A এর উপসেট হয় তবে B C A লেখা হয়।
B, A এর উপসেট অথবা B is a subset of A। উপরের উপসেটগুলোর মধ্যে {a, b} সেট A এর সমান। প্রত্যেকটি সেট নিজের উপসেট। আবার, যেকোনো সেট থেকে প সেট গঠন করা যায়। যেকোনো সেটের উপসেট।
ধরি P = {1,2,3} এবং Q = {2,3}, R = {1, 3} তাহলে P, Q এবং R প্রত্যেকে P এর উপসেট। অর্থাৎ PCP,QCP এবং REP
প্রকৃত উপসেট (Proper Subset)
কোনো সেট থেকে গঠিত উপসেটের মধ্যে যে উপসেটগুলোর উপাদান সংখ্যা প্রদত্ত সেটের উপাদান সংখ্যা অপেক্ষা কম এদেরকে প্রকৃত উপসেট বলে। যেমন, A = { 3, 4, 5, 6} এবং B = {3,5} দুইটি সেট। এখানে, B এর সব উপাদান A সেটে বিদ্যমান এবং B সেটের উপাদান সংখ্যা A সেটের উপাদান সংখ্যা থেকে কম।
.:. B, A এর একটি প্রকৃত উপসেট এবং B C A লিখে প্রকাশ করা হয়।
উপসেটের উদাহরণে Q ও R প্রত্যেকে P এর প্রকৃত উপসেট। উল্লেখ্য ফাঁকা সেট বা যেকোনো সেটের প্রকৃত উপসেট।
উদাহরণ ৫.
P = {x, y, z} এর উপসেটগুলো লিখ এবং সেগুলো থেকে প্রকৃত উপসেট বাছাই কর।
সমাধান:
দেওয়া আছে, P = {x, y, 2}
P এর উপসেটসমূহ {x, y, 2}, {x, y}, {x, 2}, {1, 2}, {c}, {3}, {2}, ∅
P এর প্রকৃত উপসেটসমূহ {x, y}, {c, 2}, {1, 2}, {r}, {u}, {2}, ∅
দ্রষ্টব্য:
কোন সেটের উপাদান সংখ্যা n হলে ওই সেটের উপসেটের সংখ্যা 2” এবং প্রকৃত উপসেটের সংখ্যা 2n – 1।

সেটের সমতা (Equivalent Set)
দুইটি সেটের উপাদান একই হলে, সেট দুইটিকে সমান বলা হয়। যেমন: A { 3, 5, 7} এবং = B = {5, 3, 3, 7} দুইটি সমান সেট এবং A = B চিহ্ন দ্বারা লেখা হয়। লক্ষ করি A = B যদি এবং কেবল যদি A⊆ B এবং B C A হয়।
আবার, A = {3, 5, 7}, B = {5, 3, 3, 7} এবং C = { 7, 7, 3, 5, 5 } হলে A, B ও C সেট তিনটি সমতা বোঝায়। অর্থাৎ, A = B = C
দ্রষ্টব্য:
সেটের উপাদানগুলোর ক্রম বদলালে বা কোনো উপাদান পুনরাবৃত্তি করলে সেটের কোনো পরিবর্তন হয় না।
সেটের অন্তর (Difference of Sets )
মনে করি, = {1, 2, 3, 4, 5} এবং B = {3,5}। সেট A থেকে সেট B এর উপাদানগুলো বাদ দিলে যে সেটটি হয় তা {1, 2, 4} এবং লেখা হয় A\ B বা A- B এবং পড়া হয় A বাদ B।
.. A B {1, 2, 3, 4, 5} {3, 5} = {1,2,4}
উদাহরণ ৬.
P {x : x, 12 এর গুণনীয়কসমূহ} এবং Q {x : x, 3 এর গুণিতক এবং = x ≤ 12} হলে P – Q নির্ণয় কর।
সমাধান:
দেওয়া আছে, P = {x : x, 12 এর গুণনীয়কসমূহ}
এখানে, 12 এর গুণনীয়কসমূহ 1, 2, 3, 4, 6, 12
.. P= {1, 2, 3, 4, 6, 12}
আবার, Q = {x : x, 3 এর গুণিতক এবং x ≤ 12}
এখানে, 12 পর্যন্ত 3 এর গুণিতকসমূহ 3, 6, 9, 12
.. Q = {3, 6, 9, 12}
.. P-Q={1, 2, 3, 4, 6, 12} {3, 6, 9, 12} = {1,2,4}
নির্ণেয় সেট: {1, 2, 4}
সার্বিক সেট (Universal Set)
আলোচনায় সংশ্লিষ্ট সকল সেট একটি নির্দিষ্ট সেটের উপসেট। যেমন: A {x, y} সেটটি B = {x, y, z} এর একটি উপসেট। এখানে, B সেটকে A সেটের সাপেক্ষে সার্বিক সেট বলে।
সুতরাং আলোচনা সংশ্লিষ্ট সকল সেট যদি একটি নির্দিষ্ট সেটের উপসেট হয় তবে ঐ নির্দিষ্ট সেটকে তার উপসেটগুলোর সাপেক্ষে সার্বিক সেট বলে।
সার্বিক সেটকে সাধারণত U দ্বারা প্রকাশ করা হয়। তবে অন্য প্রতীকের সাহায্যেও সার্বিক সেট প্রকাশ করা যায়। যেমন: সকল জোড় স্বাভাবিক সংখ্যার সেট C {2, 4, 6, … } এবং সকল স্বাভাবিক = সংখ্যার সেট N {1, 2, 3, 4, 5, 6,} হলে C সেটের সাপেক্ষে সার্বিক সেট হবে N ।
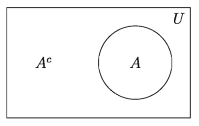
পূরক সেট (Complement of a Set)
U সার্বিক সেট এবং A সেটটি U এর উপসেট। A সেটের বহির্ভূত সকল উপাদান নিয়ে গঠিত সেটকে A সেটের পূরক সেট বলে। A এর পূরক সেটকে AS বা A’ দ্বারা প্রকাশ করা হয়। গাণিতিকভাবে A = U\A
মনে করি, P ও Q দুইটি সেট এবং P সেটের যেসব উপাদান Q সেটের উপাদান নয়, ঐ উপাদানগুলোর সেটকে P এর প্রেক্ষিতে Q এর পূরক সেট বলা হয় এবং লেখা হয় Q = P\Q
উদাহরণ ৭.
U = {1, 2, 3, 4, 5, 6, 7}, A = {2, 4, 6, 7} এবং B = {1,3,5} হলে A© ও B© নির্ণয় কর।
সমাধান: A = U\ A = {1, 2, 3, 4, 5, 6, 7} \ {2, 4, 6, 7} = {1, 3, 5 } এবং B© = U \ B = {1, 2, 3, 4, 5, 6, 7} \ {1, 3, 5} = {2, 4, 6, 7}
নির্ণেয় সেট A = {1, 3, 5} এবং B = {2, 4, 6, 7}
সংযোগ সেট (Union of Sets )
দুই বা ততোধিক সেটের সকল উপাদান নিয়ে গঠিত সেটকে সংযোগ সেট বলা হয়। মনে করি, A ও B দুইটি সেট। A ও B সেটের সংযোগকে AUB দ্বারা প্রকাশ করা হয় এবং পড়া হয় A সংযোগ B অথবা A Union B। সেট গঠন পদ্ধতিতে AUB = {x : x ∈ A অথবা E B} ।
উদাহরণ ৮.
C = {3, 4, 5} এবং D = {4, 6, 8} হলে, CUD নির্ণয় কর।
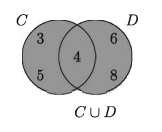
সমাধান:
দেওয়া আছে, C = { 3, 4, 5} এবং D = { 4, 6, 8}
CUD = {3, 4, 5} U { 4, 6, 8} = { 3, 4, 5, 6, 8}
নির্ণেয় সেট: {3, 4, 5, 6, 8}
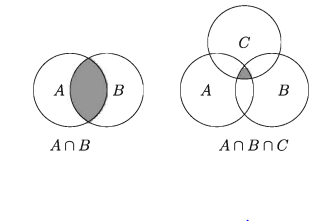
ছেদ সেট (Intersection of Sets )
দুই বা ততোধিক সেটের সাধারণ উপাদান নিয়ে গঠিত সেটকে ছেদ সেট বলে। মনে করি, A ও B দুইটি সেট। A ও B এর ছেদ সেটকে An B দ্বারা প্রকাশ করা হয় এবং পড়া হয় A ছেদ B বা A intersection B। সেট গঠন পদ্ধতিতে AnB = {x : x ∈ A এবং x ∈ B }
উদাহরণ ৯.
P = {x ∈ N : 2 < x < 6} এবং Q = {x ∈ N : x জোড় সংখ্যা এবং x ≤ 8} হলে, PnQ নির্ণয় কর।
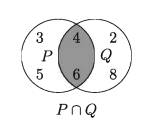
সমাধান:
দেওয়া আছে,
P = {x ∈N : 2 < < 6} = { 3, 4, 5, 6}
Q = {x ∈ N : x জোড় সংখ্যা এবং x < 8} = {2, 4, 6, 8} PnQ = {3,4,5,6} n (2,4,6,8} = {4,6}
নির্ণেয় সেট {4, 6}
নিশ্ছেদ সেট (Disjoint Set )
দুইটি সেটের মধ্যে যদি কোনো সাধারণ উপাদান না থাকে তবে সেট দুইটিকে পরস্পর নিশ্ছেদ সেট বলে। মনে করি, A ও B দুইটি সেট। AnB = Ø হলে A ও B পরস্পর নিশ্ছেদ সেট হবে।
শক্তি সেট (Power Sets )
A = {m, n} একটি সেট। A সেটের উপসেটসমূহ হলো {m, n}, {m}, {n}, ব; এখানে উপসেটসমূহের সেট {{m,n},{m}, {n}, 0} কে A সেটের শক্তি সেট বলা হয়। A সেটের শক্তি সেটকে P(A) দ্বারা প্রকাশ করা হয়। সুতরাং কোনো সেটের সকল উপসেট দ্বারা গঠিত সেটকে ঐ সেটের শক্তি সেট বলা হয়।
উদাহরণ ১০.
A = 0, B = {a}, C = {a, b} সেট তিনটির শক্তি সেটগুলোর উপাদান সংখ্যা কত?
সমাধান:
এখানে, P(A) = {0}
A সেটের উপাদান সংখ্যা শূন্য এবং এর শক্তি সেটের উপাদান সংখ্যা = 1 = 20
আবার, P(B) = {{0}, 0}
B সেটের উপাদান সংখ্যা 1 এবং এর শক্তি সেটের উপাদান সংখ্যা = 2 = 21
এবং P(C) = {{a}, {b}, {a, b}, 0}
C সেটের উপাদান সংখ্যা 2 এবং এর শক্তি সেটের উপাদান সংখ্যা = 4 = 22
সুতরাং, কোনো সেটের উপাদান সংখ্যা n হলে, ঐ সেটের শক্তি সেটের উপাদান সংখ্যা হবে 2n।
সেটের অভেদাবলী [ 1/2 ] :
সেটের অভেদাবলী [ 2/2 ] :
