গনিতের সেট

আজকে আমরা আলোচনা করবো  গনিতের সেট সম্পর্কে । যা উচ্চতর গণিতের সেট ও ফাংশন অংশের অন্তর্গত।

 

 

 গনিতের সেট (Set)

বাস্তব বা চিন্তা জগতের বস্তুর যেকোনো সুনির্ধারিত সংগ্রহকে সেট বলা হয়।

যেমন, S = {1, 4, 9, 16, 25, 36, 49, 64, 81, 100 তালিকাটি 10 থেকে বড় নয় এমন স্বাভাবিক সংখ্যার বর্গের সেট। সেটকে এভাবে তালিকার সাহায্যে বর্ণনা করাকে তালিকা পদ্ধতি বলা হয়। যে সকল বস্তু নিয়ে সেট গঠিত এদের প্রত্যেককে ঐ সেটের উপাদান বলা হয়।, A সেটের উপাদান হলে লেখা হয় x ∈ A এবং x, A সেটের উপাদান না হলে লেখা হয় ÇA। উপরোক্ত সেট S কে লেখা যায়

S = {x : 3 100 থেকে বড় নয় এমন পূর্ণবর্গ সংখ্যা)। এই পদ্ধতিকে সেট গঠন পদ্ধতি বলা হয়।

সার্বিক সেট (Universal Set)

মনে করি
S = {x : ধনাত্মক পূর্ণসংখ্যা এবং 5x ≤ 16}
T = {x : x ধনাত্মক পূর্ণসংখ্যা এবং 2 < 20}
P = {x : 2 ধনাত্মক পূর্ণসংখ্যা এবং কি < 2}

এই সেট তিনটির উপাদানসমূহ U = {x : ধনাত্মক পূর্ণ সংখ্যা} সেটটির উপাদান নিয়ে গঠিত। [U কে S, T, P সেটের জন্য সার্বিক সেট বিবেচনা করা যায়।

সেট সংক্রান্ত কোনো আলোচনায় একটি নির্দিষ্ট সেটকে সার্বিক সেট বলা হয়, যদি আলোচনাধীন সকল সেটের উপাদানসমূহ ঐ নির্দিষ্ট সেটের অন্তর্ভুক্ত হয়।

 

 

কয়েকটি বিশেষ সংখ্যা সেট

N = {1, 2, 3, · — } অর্থাৎ সকল স্বাভাবিক সংখ্যা বা ধনাত্মক পূর্ণ সংখ্যার সেট।

Z = […, – 2, -1, 0, 1, 2, 3, } অর্থাৎ সকল পূর্ণ সংখ্যার সেট।

Q = { x:x 2, যেখানে p যেকোনো পূর্ণ সংখ্যা এবং g যেকোনো ধনাত্মক পূর্ণ সংখ্যা} অর্থাৎ,
সকল মূলদ সংখ্যার সেট।

R = {x: x বাস্তব সংখ্যা} অর্থাৎ সকল বাস্তব সংখ্যার সেট।

 

উপসেট (Subset)

A ও B সেট হলে A কে B এর উপসেট বলা হয় যদি ও কেবল যদি A এর প্রত্যেক উপাদান B এর উপাদান হয় এবং একে A⊂ B লিখে প্রকাশ করা হয়। যেমন A = {2, 3}, B 2, 3, 5, 7} এর উপসেট। A, B এর উপসেট না হলে ALB লেখা হয়। যেমন A = {1,3}, B = {2,3,5,7) এর উপসেট নয়।

উদাহরণ ১.

যদি A = { ধনাত্মক পূর্ণ সংখ্যা}, B = {0} এবং X = {x : পূর্ণ সংখ্যা} হয়, তবে A, B এবং X এর মধ্যে সম্পর্ক কী?

সমাধান:

এখানে ASX, BEX, BA

ফাঁকা সেট (Empty Set)

অনেক সময় এরূপ সেট বিবেচনা করতে হয় যাতে কোনো উপাদান থাকে না। এরূপ সেটকে ফাঁকা সেট বলা হয় এবং / অথবা {} লিখে প্রকাশ করা হয় ।

উদাহরণ ২.

{x : x বাস্তব সংখ্যা এবং x2 < 0} একটি ফাঁকা সেট, কেননা কোনো বাস্তব সংখ্যার বর্গ ঋণাত্মক নয়।

উদাহরণ ৩.

F = = {x: x ২০১৪ সাল পর্যন্ত ফুটবলের বিশ্বকাপ বিজয়ী আফ্রিকার দেশ } একটি ফাঁকা সেট, কেননা আফ্রিকার কোনো দেশই ২০১৪ সাল পর্যন্ত ফুটবলের বিশ্বকাপ জয় করতে পারেনি।

 

 

সেট সমতা (Equality of Sets )

A ও B সেট যদি এমন হয় যে এদের উপাদানগুলো একই তবে A ও B একই সেট এবং তা A = B লিখে প্রকাশ করা হয়। যেমন A = {1, 2, 3, 4}, B = {1, 2, 2, 3, 4, 4, 4}। লক্ষ কর কোনো সেটে একই উপাদান বার বার থাকলেও সেটা একবার থাকার মতই বিবেচনা করা হচ্ছে। A = B হয় যদি ও কেবল যদি A ⊂ B এবং B CA হয়। সেট সমতা প্রমাণে এই তথ্য খুবই প্রয়োজনীয়।

প্রকৃত উপসেট (Proper subset)

A কে B এর প্রকৃত উপসেট বলা হয় যদি ও কেবল যদি A⊂ B এবং A + B অর্থাৎ A এর প্রত্যেক উপাদান B এরও উপাদান এবং B তে অন্তত একটি উপাদান আছে যা A তে নেই। যেমন
A = {1, 2}, B = {1, 2, 3} । A, B এর প্রকৃত উপসেট বুঝাতে ACB লেখা হয়।

ক) যেকোনো সেট A এর জন্য ACA। এর কারণ x ∈ A ⇒ x ∈ A

খ) যেকোনো সেট A এর জন্য CA। এর কারণ CA না হলে তে একটি উপাদান আছে যা A তে নাই।
কিন্তু ইহা কখনই সত্য নয় কারণ ফাঁকা সেট। অতএব Ø C A উল্লেখ্য ফাঁকা সেট বা যেকোনো সেটের প্রকৃত উপসেট।

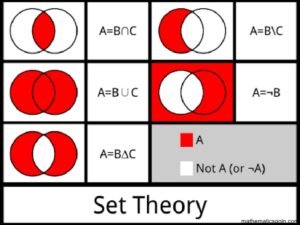
সেটের অন্তর (Difference of Sets )

A ও B সেট হলে A \ B সেটটি হচ্ছে {x: x ∈ A এবং B }।

A \ B কে A বাদ B সেট বলা হয় এবং A এর যে সকল উপাদান B তে আছে সেগুলো A থেকে বর্জন করে A\B গঠন করা হয়। A\B∈A

উদাহরণ ৪.

A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} এবং B = {0, 2, 4, 6, 8, 10} হলে A \ B = {1, 3, 5, 7, 9}।

পূরক সেট (Complementary Set)

সার্বিক সেট U এবং ACU হলে A এর পূরক সেট হচ্ছে U\A

অর্থাৎ U\A – (x:x ∈ U এবং x∉ A}।

সার্বিক সেট থেকে A সেটের উপাদানগুলো বর্জন করলেই A এর পূরক সেট পাওয়া যায় এবং তাকে A বা A লিখে প্রকাশ করা হয়।

 

 

উদাহরণ ৫.

যদি সার্বিক সেট [ সকল পূর্ণ সংখ্যার সেট হয় এবং এ সকল ঋণাত্মক পূর্ণ সংখ্যার সেট হয়, তবে (t/ সাপেক্ষে) A এর পূরক সেট A বা A = {0, 1, 2, 3, … }

শক্তি সেট (Power Set)

A সেটের সকল উপসেটের সেটকে A এর শক্তি সেট বলা হয় এবং P(A) দ্বারা নির্দেশ করা হয়। উল্লেখ্য যে CA। কাজেই , P(A) এরও উপাদান।

A সেট

P(A) শক্তি সেট

A = Ø
P(A) = {Ø}
A = (a) P(A) = {Ø,A) |
A = (a,b)
P(A) = {0, {a}, {b}, A}
A = {a, b, c}
P(A) = {≈, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, A}

উদাহরণ 6.

A = {a, b} এবং B = {h, c} হলে দেখাও যে, P(A) UP(B) P(AUB)।

সমাধান:

এখানে, P(A) = (0, (a}, {6}, { a, b } } P(B) = (0, (b}, {c}, {b, c}} ।
P(A) UP(B) = {0, {a}, {b}, {c}, {a, b}, {b,c}} AUB (a,b,c), P(AUB) – {Ø, {a}, {b}, {c}, {a, b), (a, c), (b, c), (a, b, c)} |

সুতরাং, P(A) UP(B) P(AUB) |

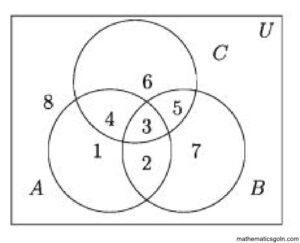
ভেনচিত্র (Venn Diagram)

সেট সংক্রান্ত তথ্যাদি অনেক সময় চিত্রে প্রকাশ করা সুবিধাজনক। উদ্ভাবক John Venn (১৮৩৪ ১৯২৩) এর নামানুসারে এরূপ চিত্রকে ভেনচিত্র বলা হয়। গণিত বইতে এ সম্পর্কে বিশদ আলোচনা করা হয়েছে।

উদাহরণ ৭.

সার্বিক সেট L এর সাপেক্ষে A সেট এর পূরক সেট A’ এর চিত্ররূপ :

 

সেটের সংযোগ (Union of Sets )

A ও B সেট হলে এদের সংযোগ সেট হচ্ছে AUB (2:26 A অথবা B অর্থাৎ A ও B উভয় সেটের সকল উপাদান নিয়ে গঠিত সেটই AUB।

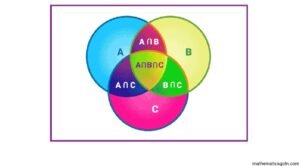
সেটের ছেদ (Intersection of Sets )

A ও B সেট হলে এদের ছেন সেট হচ্ছে An B = {x: x ∈ A এবং E B }। অর্থাৎ A ও B সেটের সকল সাধারণ উপাদান নিয়ে গঠিত সেটই A∩B

উদাহরণ ৮.

সার্বিক সেট = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} এর দুইটি উপসেট A = {x: x মৌলিক সংখ্যা} এবং B = {x : বিজোড় সংখ্যা}।

তাহলে A = {2, 3, 5, 7} এবং B = {1, 3, 5, 7, 9) ।

সুতরাং AUB = {1, 2, 3, 5, 7, 9), AnB – 3, 5, 7},

A’ = {0,1,4,6,8,9), B’ = {0,2,4,6,8},

A’ U B’ = {0, 1, 2, 4, 6, 8, 9], A’ ∩ B’ = {0, 4, 6, 8}.

(A∩B) = {0, 1, 2, 4, 6, 8, 9], (AUB) = {0, 4, 6, 8} ।

নিচ্ছেদ সেট (Disjoint Set)

যদি A ও B সেট এমন হয় যে AnB = a, তবে A ও B কে নিশ্ছেদ সেট বলা হয়।

উদাহরণ ৯.

A = {x : ধনাত্মক পূর্ণ সংখ্যা} এবং B = {z ঋণাত্মক পূর্ণ সংখ্যা} হলে A ও B সেটদ্বয় নিশ্ছেদ, কেননা A∩B = ∅

উদাহরণ ১০.

A = {x: x∊R এবং 0 ≤ x ≤ 2 } এবং B = {x: x∊N এবং 0 ≤ x ≤ 2 } হলে B⊆A,AUB,A, A∩B = B = (1,2)

উদাহরণ ১১.

A = {x: x∊R এবং 15 15 2} এবং B = {x: x ∈ R এবং 0 < 1 < 1} হলে, AUB = {n: R S 2} এবং AB = B অর্থাৎ A ও B নিশ্ছেদ।

কার্তেসীয় গুণজসেট (Cartesian Product Set)

দুইটি সেট A এবং B এর কার্তেসীয় গুণজ Ax B = {(2, y ) : x ∊ A এবং y ∊ B ) ।

উদাহরণ ১২.

A = {1, 2}, B = {a, b, c ) দুইটি সেট। সুতরাং এই দুইটি সেটের কার্তেসীয় গুণজ সেট A × B = {(1, a), (1, 6), (1, 2), (2, 0), (2, 6), (2, 0)}।

আরও দেখুনঃ

• মাধ্যমিক ৯ম ও ১০ম শ্রেণি উচ্চতর গণিত, ২০২৩, এনসিটিবি, বাংলা