আমাদের আজকের আলোচনার বিষয় গসাগুর খেলা – যা মৌলিক উৎপাদকের গাছ এর অন্তর্ভুক্ত। গণিত হল জ্ঞানের একটি ক্ষেত্র যাতে সংখ্যা, সূত্র এবং সম্পর্কিত কাঠামো, আকার এবং সেগুলির মধ্যে থাকা স্থানগুলি এবং পরিমাণ এবং তাদের পরিবর্তনগুলি অন্তর্ভুক্ত থাকে। এই বিষয়গুলি যথাক্রমে সংখ্যা তত্ত্বের প্রধান উপশাখা,বীজগণিত, জ্যামিতি, এবং বিশ্লেষণ। তবে একাডেমিক শৃঙ্খলার জন্য একটি সাধারণ সংজ্ঞা সম্পর্কে গণিতবিদদের মধ্যে কোন সাধারণ ঐকমত্য নেই।
গণিতে সংখ্যা ও অন্যান্য পরিমাপযোগ্য রাশিসমূহের মধ্যকার সম্পর্ক বর্ণনা করা হয়। গণিতবিদগন বিশৃঙ্খল ও অসমাধানযুক্ত সমস্যাকে শৃঙ্খলভাবে উপস্থাপনের প্রক্রিয়া খুঁজে বেড়ান ও তা সমাধানে নতুন ধারণা প্রদান করে থাকেন।গাণিতিক প্রমাণের মাধ্যমে এই ধারণাগুলির সত্যতা যাচাই করা হয়। গাণিতিক সমস্যা সমাধান সম্পর্কিত গবেষণায় বছরের পর বছর, যুগের পর যুগ বা শত শত বছর পর্যন্ত লেগে যেতে পারে। গণিতের সার্বজনীন ভাষা ব্যবহার করে বিজ্ঞানীরা একে অপরের সাথে ধারণার আদান-প্রদান করেন। গণিত তাই বিজ্ঞানের ভাষা।
গসাগুর খেলা
তোমরা গসাগু নির্ণয়ের একাধিক পদ্ধতি সম্পর্কে পূর্বের শ্রেণিতে জেনেছ। নিচের পদ্ধতিটাও নিশ্চয়ই তোমাদের অজানা নয়।
 গসাগু = ২ × ৩ = ৬
গসাগু = ২ × ৩ = ৬
কিন্তু কেন এভাবে গসাগু পাওয়া যায় সেটা কি বলতে পারবে?
চলো গসাগু মানে কী সেটা একটু বোঝার চেষ্টা করি।
গসাগু’র পূর্ণরূপ হচ্ছে গরিষ্ঠ সাধারণ গুণনীয়ক।
“একটি সংখ্যার সবগুলো মৌলিক উৎপাদক যদি অন্য একটি সংখ্যার মধ্যে থাকে তাহলে ১ম সংখ্যা ২য় সংখ্যার ‘গুণনীয়ক হবে।”
তাহলে দুইটি সংখ্যার সাধারণ গুণনীয়ক হবে এমন একটি সংখ্যা যার সবগুলো মৌলিক উৎপাদকই ঐ দুইটি সংখ্যার মৌলিক উৎপাদকের গাছে থাকবে।
এখন, গসাগু অর্থাৎ গরিষ্ঠ সাধারণ গুণনীয়ক হচ্ছে সবচেয়ে বড় সাধারণ গুণনীয়ক। সেক্ষেত্রে তোমরা দুইটি সংখ্যারই মৌলিক উৎপাদকের গাছে পাওয়া যাবে এমন সবগুলো মৌলিক উৎপাদক খুঁজে বের করলে তাদের গুণফলই হবে গসাগু। চাইলে চেষ্টা করে দেখতে পারো এই গুণফলের চেয়ে বড় কোন সংখ্যা নিলে সেটা দুইটি সংখ্যারই সাধারণ উৎপাদক হতে পারে কিনা?
এবার ভেবে দেখতো মৌলিক উৎপাদকের গাছের সাহায্যে কীভাবে গসাগু ‘নির্ণয়ের খেলাটি খেলতে হবে? গসাগু’র খেলার নিয়ম:
- দুইটি সংখ্যার মৌলিক ‘উৎপাদকের গাছ আঁকো।
- দুইটি সংখ্যার মৌলিক ‘উৎপাদকের গাছেই আছে এমন মৌলিক ‘উৎপাদকগুলো চিহ্নিত করো। এগুলো হচ্ছে ঐ সংখ্যা দুইটির সাধারণ মৌলিক ‘উৎপাদক।
- এবার সাধারণ মৌলিক ‘উৎপাদকগুলোর গুণফলই হবে ঐ সংখ্যার গসাগু।
ছবিতে গসাগু’র খেলার মাধ্যমে ১৮ ও ১২ এর গসাগু নির্ণয় দেখে নাও।
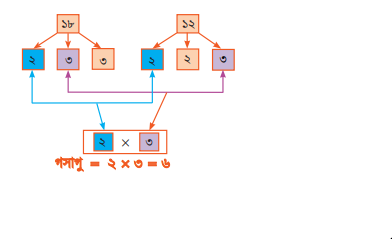
পাশের দেখানো মৌলিক ‘উৎপাদকের গাছের সাহায্যে গসাগু নির্ণয়ের পদ্ধতি এবং গসাগু খেলা অংশের শুরুতে দেখানো পদ্ধতির মধ্যে কোনো মিল খুঁজে পাচ্ছ কি?
নিচের ছবিটা দেখলে খুব সহজেই বুঝতে পারবে যে দুটি পদ্ধতি আসলে একই।
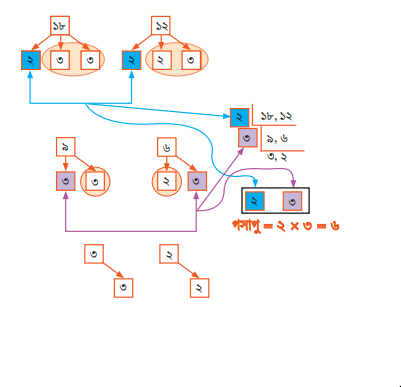
‘১ মৌলিক উৎপাদকের গাছে না থাকলেও কিছু সব সংখ্যার উৎপাদক/গুণনীয়ক।’
যদি দুইটি সংখ্যার মধ্যে ১ ছাড়া অন্য কোনো সাধারণ গুণনীয়ক না থাকে অর্থাৎ তাদের গসাগু ১ হয় তাহলে সংখ্যা দুইটিকে আমরা সহমৌলিক সংখ্যা (Co-prime numbers) বলি।
যেমন: ৪ ও ৯ এর গসাগু ১। তাই ৪ ও ৯ পরস্পর সহমৌলিক।
