ঘন জ্যামিতির ঘনবস্তু

আজকে আমরা ঘন জ্যামিতির ঘনবস্তু আলোচনা করবো। যা উচ্চতর গণিতের  ঘন জ্যামিতি অংশের অন্তর্গত।

 

 

ঘন জ্যামিতির ঘনবস্তু

আমরা জানি, একখানা বই বা একখানা ইট বা একটি বাক্স বা একটি গোলাকার বল সবই ঘনবস্তু । তারা প্রত্যেকেই কিছু পরিমান স্থান (space) দখল করে থাকে। আবার একখণ্ড পাথর বা কাঠ, ইটের একটি খণ্ড, কয়লার টুকরা, এঁটেল মাটির শুকনা খণ্ড ইত্যাদিও ঘনবস্তুর উদাহরণ। তবে এগুলো বিষম ঘনবস্তু।

সমতল অথবা বক্রতল দ্বারা বেষ্টিত শূন্যের কিছুটা স্থান দখল করে থাকে এরূপ বস্তুকে ঘনবস্তু (solid) বলা হয়। সমতলস্থ কোনো স্থানকে বেষ্টন করতে হলে যেমন কমপক্ষে তিনটি সরল রেখা দরকার তেমনি জাগতিক কোনো স্থানকে বেষ্টন করতে হলে অন্তত চারটি সমতল দরকার। এই তলগুলো ঘনবস্তুর তল বা পৃষ্ঠতল (surface) এবং এদের দুটি সমতল যে রেখায় ছেদ করে, তাকে ঐ ঘনবস্তুর ধার (edge) বলা হয়। একটি বাক্সের বা একখানা ইটের ছয়টি পৃষ্ঠতল আছে এবং বারটি ধার আছে। একটি ক্রিকেট বল মাত্র একটি বক্রতল দ্বারা আবদ্ধ।

সুষম ঘনবস্তুর আয়তন ও তলের ক্ষেত্রফল

১. আয়তিক ঘন বা আয়তাকার ঘনবস্তু (Rectangular Parallelopiped)

 

 

তিনজোড়া সমান্তরাল সমতল দ্বারা আবদ্ধ ঘনবস্তুকে সামান্তরিক ঘনবস্তু বলা হয়। এই ছয়টি সমতলের প্রত্যেকটি একটি সামান্তরিক এবং বিপরীত পৃষ্ঠগুলো সর্বতোভাবে সমান। সামান্তরিক ঘনবস্তুর ছয়টি তলে বিভক্ত বারটি ধার আছে।

যে সামান্তরিক ঘনবস্তুর পৃষ্ঠতলগুলো আয়তক্ষেত্র, তাকে আয়তাকার ঘনবস্তু বলা হয়। যে আয়তাকার ঘনবস্তুর পৃষ্ঠতলগুলো বর্গক্ষেত্র, তাকে ঘনক বলা হয়। উপরোক্ত চিত্রে আয়তাকার ঘনবস্তুর এবং ঘনকের পৃষ্ঠগুলো ABCD, A’B’C’D’, BCC’B’, ADD’A’, ABB’A’, DCC’D’ এবং ধারগুলো AB, AB, CD, CD, BC, BC’, AD, A’D’, AA’, BB’, CC’, DD’। তবে চিত্রে কেবল একটি কর্ণ BD’ দেখানো হয়েছে, অন্যগুলো অনুরূপভাবে আঁকতে হবে।

মনে করি, আয়তাকার ঘনবস্তুর দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে AB = a একক, AD = b একক এবং AA’ = c একক।

ক) আয়তাকার ঘনবস্তুর সমগ্র তলের ক্ষেত্রফল (Area of the whole surface)
= ছয়টি পৃষ্ঠের ক্ষেত্রফলের সমষ্টি

= 2 (ABCD তলের ক্ষেত্রফল + ABB’A’ তলের ক্ষেত্রফল + ADD’A’ তলের ক্ষেত্রফল)

= 2 (ab + ac + bc) বর্গ একক = 2 (ab + bc + ca) বর্গ একক

খ) আয়তন (Volume) = AB × AD x AA’ ঘন একক = abc ঘন একক

গ) কর্ণ BD’ = √(BD2 + DD2) = √(AB2+ AD2+DD’2) = √(a2 + b2 + c2) = একক

 

 

২. ঘনক (Cube) আকৃতির ঘনবস্তু

ঘনকের ক্ষেত্রে, a = b = c, অতএব

ক) সমগ্র তলের ক্ষেত্রফল = 2 (a2 + a2 + c2) = 6a2 বর্গ একক

খ) আয়তন = a . a . a = a3 ঘন একক

গ) কর্ণ = √(a2 + a2 + a2) = √3a একক

উদাহরণ ১.

একটি আয়তাকার ঘনবস্তুর দৈর্ঘ্য, প্রস্থ ও উচ্চতার অনুপাত 4 : 3 : 2 এবং তার সমগ্র তলের ক্ষেত্রফল 468 বর্গমিটার হলে, তার কর্ণ ও আয়তন নির্ণয় কর।

সমাধান:

মনে করি, দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 4x, 3x ও 2x মিটার।

তাহলে, 2(4x .3x + 3x .2x + 2x .4x ) = 468

বা, 52×2 = 468

বা, x2 = 9

x = 3

ঘনবস্তুর দৈর্ঘ্য 12 মিটার, প্রস্থ 9 মিটার এবং উচ্চতা 6 মিটার

কর্ণের দৈর্ঘ্য √(122 +92 + 62) মিটার

= √(144 +81 +36)

= √261 মিটার ≈ 16.16 মিটার (প্রায়)

এবং আয়তন = 12 x 9 x 6 = 648 ঘনমিটার।

৩. প্রিজম (Prism )

যে ঘনবস্তুর দুই প্রান্ত সর্বসম ও সমান্তরাল বহুভুজ দ্বারা আবদ্ধ এবং অন্যান্য তলগুলো সামান্তরিক তাকে প্রিজম বলে। প্রিজমের দুই প্রান্তকে ইহার ভূমি এবং অন্যান্য তলগুলোকে পার্শ্বতল বলে। সবগুলো পার্শ্বতল আয়তাকার হলে প্রিজমটিকে খাড়া বা সমপ্রিজম এবং অন্যক্ষেত্রে প্রিজমটিকে তীর্যক প্রিজম বলা হয়। বাস্তব ক্ষেত্রে খাড়া প্রিজমই অধিক ব্যবহৃত হয়। ভূমির তলের নামের উপর নির্ভর করে কোন প্রিজমের নামকরণ করা হয়। যেমন, ত্রিভুজাকার প্রিজম, চতুর্ভুজাকার প্রিজম, পঞ্চভুজাকার প্রিজম ইত্যাদি।

 

 

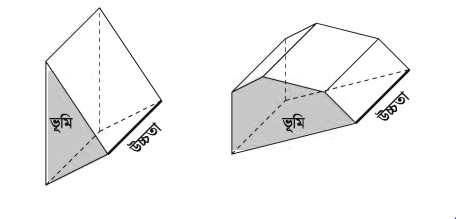
ভূমি সুষম বহুভূজ হলে প্রিজমকে সুষম প্রিজম (regular prism) বলে। ভূমি সুষম না হলে ইহাকে বিষম প্রিজম (irregular prism) বলা হয়। সংজ্ঞানুসারে আয়তাকার ঘনবস্তু ও ঘনক উভয়কেই প্রিজম বলা হয়। কাঁচের তৈরি খাড়া ত্রিভুজাকার প্রিজম আলোকরশ্মির বিচ্ছুরণের জন্য ব্যবহৃত হয়।

ক) প্রিজমের সমগ্রতলের ক্ষেত্রফল

= 2 (ভূমির ক্ষেত্রফল) + পার্শ্বতলগুলোর ক্ষেত্রফল

= 2 (ভূমির ক্ষেত্রফল) + ভূমির পরিসীমা × উচ্চতা

খ) আয়তন = ভূমির ক্ষেত্রফল × উচ্চতা

উদাহরণ ২.

একটি ত্রিভুজাকার প্রিজমের ভূমির বাহুগুলোর দৈর্ঘ্য যথাক্রমে 3, 4 ও 5 সে.মি. এবং উচ্চতা ৪ সে.মি.। ইহার সমগ্রতলের ক্ষেত্রফল ও আয়তন নির্ণয় কর।

সমাধান:

প্রিজমের ভূমির বাহুগুলোর দৈর্ঘ্য যথাক্রমে 3,4 ও 5 সে.মি.।

যেহেতু 32 + 42 = 52, ইহার ভূমি একটি সমকোণী ত্রিভুজ যার ক্ষেত্রফল = 1/2 x 4 x 3 = 6 বর্গ = সে.মি. সুতরাং, প্রিজমটির সমগ্রতলের ক্ষেত্রফল = 2 x 6 + (3+4+ 5 ) x 8 = 12 +96 = 108 বর্গ সে.মি. এবং ইহার আয়তন = 6 x 8 = 48 ঘন সে.মি.

অতএব প্রিজমটির সমগ্রতলের ক্ষেত্রফল 108 বর্গ সে.মি. এবং আয়তন 48 ঘন সে.মি.।

৪. পিরামিড (Pyramid)

বহুভুজের উপর অবস্থিত যে ঘনবস্তুর একটি শীর্ষবিন্দু থাকে এবং যার পার্শ্বতলগুলোর প্রত্যেকটি ত্রিভুজাকার তাকে পিরামিড বলে।

 

 

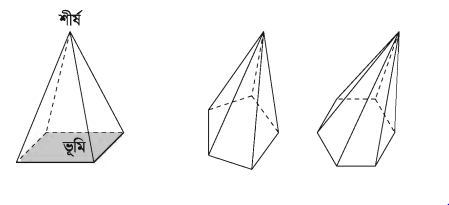
পিরামিডের ভূমি যেকোনো আকারের বহুভুজ এবং তার পার্শ্বতলগুলোও যেকোনো ধরনের ত্রিভুজ হতে পারে। তবে ভূমি সুষম বহুভুজ এবং পার্শ্বতলগুলো সর্বসম ত্রিভুজ হলে তাকে সুষম পিরামিড বলা হয়। সুষম পিরামিডগুলো খুবই দৃষ্টিনন্দন। শীর্ষবিন্দু ও ভূমির যেকোনো কৌণিক বিন্দুর সংযোজক রেখাকে পিরামিডের ধার বলে। শীর্ষ হতে ভূমির উপর অঙ্কিত লম্বদৈর্ঘ্যকে পিরামিডের উচ্চতা বলা হয়। তবে আমরা পিরামিড বলতে সচরাচর বর্গাকার ভূমির উপর অবস্থিত চারটি সর্বসম ত্রিভুজ দ্বারা বেষ্টিত ঘনবস্তুকেই বুঝি। এই ধরনের পিরামিডের বহুল ব্যবহার আছে।

চারটি সমবাহু ত্রিভুজ দ্বারা বেষ্টিত ঘনবস্তুকে সুষম চতুস্থলক (regular tetrahedron) বলে যা একটি পিরামিড। এই পিরামিডের 3 + 3=  6 টি ধার ও 4 টি কৌণিক বিন্দু আছে। ইহার = শীর্ষ হতে ভূমির উপর অঙ্কিত লম্ব ভূমির ভরকেন্দ্রে পতিত হয়।

ক) পিরামিডের সমগ্রতলের ক্ষেত্রফল = ভূমির ক্ষেত্রফল + পার্শ্বতলগুলোর ক্ষেত্রফল

কিন্তু পার্শ্বতলগুলো সর্বসম ত্রিভুজ হলে,

পিরামিডের সমগ্রতলের ক্ষেত্রফল = ভূমির ক্ষেত্রফল + 1/2(ভূমির পরিধি × হেলানো  উচ্চতা)

কোনো পিরামিডের উচ্চতা h, ভূমিক্ষেত্রের অন্তবৃত্তের ব্যাসার্ধ r এবং হেলানো উচ্চতা l হলে, l = √(h² + r2 )

খ) আয়তন  = 1/3 × ভূমির ক্ষেত্রফল × উচ্চতা

 

 

উদাহরণ ৩.

10 সে.মি. বাহুবিশিষ্ট বর্গাকার ভূমির উপর অবস্থিত একটি পিরামিডের উচ্চতা 12 সে.মি.। ইহার সমগ্রতলের ক্ষেত্রফল ও আয়তন নির্ণয় কর।

সমাধান:

পিরামিডের ভূমির কেন্দ্রবিন্দু হতে যেকোনো বাহুর লম্ব দূরত্ব r = 10/2সে.মি. = 5 সে.মি. , পিরামিডের উচ্চতা 12 সে.মি.।

অতএব ইহার যেকোনো পার্শ্বতলের হেলানো উচ্চতা = ✓(h2 + r2) = ✓(122 + 52)

= √(144 + 25) = ✓169 = 13 সে.মি.।

পিরামিডের সমগ্রতলের ক্ষেত্রফল = [10 × 10 + 1/2 ( 4 x 10) × 13] বর্গ সে.মি.

= 100 + 260 = 360 বর্গ সে.মি.

এবং ইহার আয়তন  = 1/3 x (10 x 10) × 12 ঘন সে.মি. =  10 x 10 x 4 = 400 ঘন সে.মি.।

অতএব পিরামিডটির সমগ্রতলের ক্ষেত্রফল 360 বর্গ সে.মি. এবং আয়তন 400 ঘন সে.মি.।

৫. সমবৃত্তভূমিক কোণক (Right circular cone)

কোনো সমকোণী ত্রিভুজের সমকোণ সংলগ্ন একটি বাহুকে অক্ষ (axis) ধরে তার চতুর্দিকে ত্রিভুজটিকে একবার ঘুরিয়ে আনলে যে ঘনবস্তু উৎপন্ন হয়, তাকে সমবৃত্তভূমিক কোণক বলা হয়।

 

 

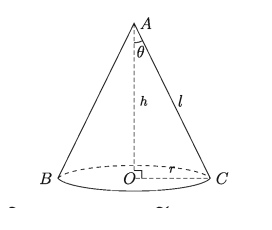
চিত্রে, OAC সমকোণী ত্রিভুজকে OA রেখার চতুর্দিকে ঘোরানোর ফলে ABC সমবৃত্তভূমিক কোণক উৎপন্ন হয়েছে। এক্ষেত্রে ত্রিভুজের শীর্ষকোণ LOAC = 0 হলে, কে কোণকের অর্ধশীর্ষকোণ (semi vertical angle) বলা হয়।

কোণকের উচ্চতা OA = h, ভূমির ব্যাসার্ধ OC = r এবং হেলানো উচ্চতা AC হলে = l হলে

ক) বক্রতলের ক্ষেত্রফল = 1/2× ভূমির পরিধি × হেলানো উচ্চতা

= 1 /2  x 2πr x l = πrl বর্গ একক

খ) সমগ্রতলের ক্ষেত্রফল = বক্রতলের ক্ষেত্রফল + ভূমিতলের ক্ষেত্রফল

= πrl + πr2 = πr (r + 1) বর্গ একক

গ) আয়তন = 1/3 × ভূমির ক্ষেত্রফল × উচ্চতা

= 1/3πr2h ঘন একক। [আয়তনের এই সূত্রটি নির্ণয় পদ্ধতি উচ্চতর শ্রেণিতে শিখানো হবে]

উদাহরণ ৪.

একটি সমবৃত্তভূমিক কোণকের উচ্চতা 12 সে.মি. এবং ভূমির ব্যাস 10 সে.মি. হলে তার হেলানো উচ্চতা, বক্রতলের ও সমগ্রতলের ক্ষেত্রফল এবং আয়তন নির্ণয় কর।

সমাধান:

ভূমির ব্যাসার্ধ r = 10/2 সে.মি. -= 5 সে.মি.

হেলানো উচ্চতা l = ✓(h2 + r2) = ✓(122 + 52)  = 13 সে.মি.

বক্রতলের ক্ষেত্রফল  = πrl = π x 5 × 13 = 204.2035 বর্গ সে.মি. (প্রায়)

সমগ্রতলের ক্ষেত্রফল = πr ( 1 + r) = π x 5 x ( 13 + 5 ) = 282.7433 বর্গ সে.মি. (প্রায়)

আয়তন = 1/3πr2h = 1/3 π x 52 x 12 = 314.1593 ঘন সে.মি. (প্রায়)।

৬. গোলক ( Sphere)

কোনো অর্ধবৃত্ত ক্ষেত্রের ব্যাসকে অক্ষ ধরে ঐ ব্যাসের চতুর্দিকে অর্ধবৃত্ত ক্ষেত্রকে একবার ঘুরিয়ে আনলে যে ঘনবস্তু উৎপন্ন হয় তাকে গোলক বলে। অর্ধবৃত্তটির কেন্দ্রই গোলকের কেন্দ্র। এই ঘূর্ণনের ফলে অর্ধবৃত্ত যে তল উৎপন্ন করে তাই হল গোলকের তল।

 

 

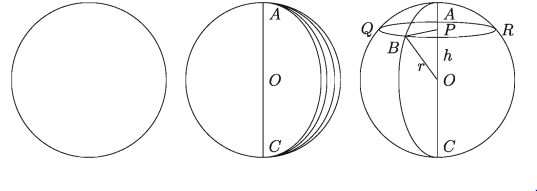
CQAR গোলকের কেন্দ্র O, ব্যাসার্ধ OA = OB = OC এবং কেন্দ্র O থেকে h দূরত্বে P = বিন্দুর মধ্য দিয়ে OA রেখার সাথে লম্ব হয় এরূপ একটি সমতল গোলকটিকে ছেদ করে একটি QBR বৃত্ত উৎপন্ন করেছে। এই বৃত্তের কেন্দ্র P এবং ব্যাসার্ধ PB।

OB² = OP² + PB²

PB2 = OB² – OP² = r2 – h2

গোলকের ব্যাসার্ধ r হলে,

ক) গোলকের পৃষ্ঠতলের ক্ষেত্রফল = 4πr²

খ) আয়তন = 4/3πr3 ঘন একক

গ) h উচ্চতায় তলচ্ছেদে উৎপন্ন বৃত্তের ব্যাসার্ধ = √(r2 – h2) একক ।

উদাহরণ ৫.

2 4 সে.মি. ব্যাসের একটি লৌহ গোলককে পিটিয়ে সে.মি. পুরু একটি বৃত্তাকার 3 লৌহপাত প্রস্তুত করা হল। ঐ পাতের ব্যাসার্ধ কত?

সমাধান:

লৌহ গোলকের ব্যাসার্ধ  = 4/ 2 সে.মি.।  = 2 সে.মি.

তার আয়তন = = 4/3π x 23 = 32/3π  ঘন সে.মি.।

মনে করি, পাতের ব্যাসার্ধ = r সে.মি.। পাতটি 2/3 সে.মি. পুরু।

.: পাতের আয়তন = πr2 x 2/3 ঘন সে.মি.  ।  = 2/3πr2

শর্তানুসারে, 2/3πr2 =  32/3π

বা, r2 = 16

বা, r = 4

পাতের ব্যাসার্ধ = 4 সে.মি.

 

 

উদাহরণ ৬.

সমান উচ্চতা বিশিষ্ট একটি সমবৃত্তভূমিক কোণক, একটি অর্ধ গোলক ও একটি সিলিন্ডার সমান সমান ভূমির উপর অবস্থিত। দেখাও যে, তাদের আয়তনের অনুপাত 1 : 2 : 3।

সমাধান:

মনে করি, সাধারণ উচ্চতা ও ভূমির ব্যাসার্ধ যথাক্রমে h এবং r একক। যেহেতু অর্ধ গোলকের উচ্চতা ও ব্যাসার্ধ সমান সুতরাং,

h = r

তাহলে কোণকের আয়তন = 1/3πr2h  ঘন একক  = 1/3πr3  ঘন একক

অর্ধ গোলকের আয়তন = 1/2(4/3πr3)  ঘন একক  = 2/3πr3 ঘন একক

সিলিন্ডারের আয়তন = πr2h = πr3 ঘন একক

.:. নির্ণেয় অনুপাত = 1/3πr3 : 2/3πr3 : πr3 = 1/3 : 2/3 : 1 = 1: 2: 3

উদাহরণ ৭.

একটি আয়তাকার লৌহ ফলকের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 10, 8 ও সে.মি.। এই ফলকটিকে গলিয়ে – সে.মি. ব্যাসার্ধ বিশিষ্ট কতগুলো গোলাকার গুলি প্রস্তুত করা যাবে?

সমাধান:

লৌহ ফলকের আয়তন = 10 x 8 x 11/2 ঘন সে.মি.

= 440 ঘন সে.মি.

মনে করি, গুলির সংখ্যা = n.

n সংখ্যক গুলির আয়তন = n x 4/3π (1/2)3 =  nπ/6  ঘন সে.মি.

প্রশ্নানুসারে, nπ/6 = 440 বা, n = (440 x 6)/π = 840.34

.:. নির্ণেয় গুলির সংখ্যা 840 টি।

উদাহরণ ৮

একটি সমবৃত্তভূমিক কোণকের আয়তন V, বক্রতলের ক্ষেত্রফল S, ভূমির ব্যাসার্ধ r, উচ্চতা । এবং অর্ধ শীর্ষকোণ α হলে দেখাও যে,
ক) S = πh²tanα/ cosα =  πr3sina বর্গ একক

খ) V = 1/3πh3tanα = πr3/3tanα ঘন একক

 

 

সমাধান:

উপরের চিত্রে, কোণকের উচ্চতা OA = h হেলানো উচ্চতা AC = l, ভূমির ব্যাসার্ধ OC = r এবং অর্ধ শীর্ষকোণ ∠OAC = α ।

সুতরাং, হেলানো উচ্চতা = √(h2 +r2)

চিত্র হতে দেখা যায় যে, tanα = r/h

r= htanα, h = r/cotα = rtanα

ক ) S = πrl =  πг√(h²+h²tan²α) =  πгh√(1 + tan²α)  = πrh√sес2α  = πrhsесα = π(htanα)hsесα = πh2tanα/cosα বর্গ একক

আবার , S = πrhsecα = 9πr/cosα)rcotα =  πr² cosα/ cosα sinα  = πr² sinα বর্গ একক

খ) V = 1/3πr²h = 1/3π(htanα)2h = 1/3πh3tan²α = 1/3π (r/tanα)3 tan²α  = πr3/3 tanαঘন একক

৭. যৌগিক ঘনবস্তু (Compound solid)

দুইটি ঘনবস্তুর সমন্বয়ে গঠিত ঘনবস্তুকে যৌগিক ঘনবস্তু বলে। নিম্নে যৌগিক ঘনবস্তুর কিছু উদাহরণ দেয়া হল:

ক) একটি আয়তাকার ঘনবস্তুর উপরের তল যদি একটি খাড়া প্রিজমের কোনো একটি তলের সমান হয় তবে ঘনবস্তুর উপর মিলিয়ে প্রিজমটি বসালে একটি যৌগিক ঘনবস্তু হয়।

খ) একটি প্রিজমের ভূমি ও একটি চতুস্তলকের ভূমি সর্বসম হলে এবং চতুস্তলকটিকে প্রিজমের উপর বসালে একটি যৌগিক ঘনবস্তু হয়।

গ) একটি অর্ধগোলকের ব্যাসার্ধ ও একটি সমবৃত্তভূমিক কোণকের ভূমির ব্যাসার্ধ সমান হলে এবং কোণকটিকে অর্ধগোলকের উপর বসালে একটি নতুন ঘনবস্তু সৃষ্টি হয়।

ঘ) দুইটি অর্ধগোলক ও একটি সমবৃত্তভূমিক সিলিন্ডারের সমন্বয়ে গঠিত যৌগিক ঘনবস্তুকে ক্যাপসুল বলা যেতে পারে।

এভাবে দুই বা দুইয়ের অধিক ঘনবস্তুর সমন্বয়ে বিভিন্ন প্রকারের যৌগিক ঘনবস্তু তৈরি করা যায়। অনেক দৃষ্টিনন্দন স্থাপনাও যৌগিক ঘনবস্তু। ব্যায়াম করার অনেক উপকরণও একাধিক ঘনবস্তুর সমন্বয়ে তৈরি করা হয়।

 

 

উদাহরণ ৯.

একটি ক্যাপসুলের দৈর্ঘ্য 15 সে.মি.। ইহার সিলিন্ডার আকৃতির অংশের ব্যাসার্ধ 3 সে.মি. হলে, সমগ্রতলের ক্ষেত্রফল ও আয়তন নির্ণয় কর।

সমাধান:

ক্যাপসুলের সম্পূর্ণ দৈর্ঘ্য 15 সে.মি.। যেহেতু ক্যাপসুলের দুই প্রান্ত অর্ধগোলকাকৃতির, সেহেতু ইহার সিলিন্ডার আকৃতির অংশের দৈর্ঘ্য,l  15 – ( 3 + 3) = 9 সে.মি.।

সুতরাং ক্যাপসুলের সমগ্রতলের ক্ষেত্রফল = দুই প্রান্তের অর্ধগোলাকৃতি অংশের পৃষ্ঠতলের ক্ষেত্রফল + সিলিন্ডার আকৃতির অংশের পৃষ্ঠতলের ক্ষেত্রফল

= 2 × 1/2 × 4/3πr2 + πr2l = 4/3π( 3 )3 + π(3)2 x 9 = 90π = 282.74 বর্গ সে.মি. (প্রায়)।

এবং ক্যাপসুলটির আয়তন

2 × 1/2 × 4/3πr3 × 4/3π(3)3 + π(3)2 × 9 = 117π =  367.57 ঘন সে.মি. (প্রায়)।

 

 

উদাহরণ ১০.

একটি লোহার ফাঁপা গোলকের বাইরের ব্যাস 15 সে.মি. এবং বেধ 2 সে.মি.।

ক) গোলকের ফাঁপা অংশের আয়তন নির্ণয় কর।

খ) গোলকে ব্যবহৃত লোহা দিয়ে একটি নিরেট গোলক তৈরি করা হল। নিরেট গোলকের পৃষ্ঠতলের ক্ষেত্রফল নির্ণয় কর।

গ) নিরেট গোলকটি একটি ঘনক আকৃতির বাক্সে ঠিকভাবে এঁটে গেল। বাক্সটির অনধিকৃত অংশের আয়তন নির্ণয় কর।

সমাধান:

ক) দেওয়া আছে, গোলকের বাইরের ব্যাস 15 সে.মি.

গোলকের বাইরের ব্যাসার্ধ : = 15 /2 সে.মি. = 7.5 সে.মি. এবং গোলকের বেধ 2 সে.মি.

গোলকের ফাঁপা অংশের ব্যাসার্ধ = (7.5 – 2 ) সে.মি. = 5.5 সে.মি.

গোলকের ফাঁপা অংশের আয়তন = = 4/3πr3 =  4/3π x (5.5) 3 = 696.9116 ঘন সে.মি. (প্রায়)

খ) এখানে, গোলকের ব্যাসার্ধ 7.5 সে.মি.

গোলকের আয়তন = 4/3π x (7.5 ) 3 = 1767.15 ঘন সে.মি. (প্রায়)

গোলকে ব্যবহৃত লোহার আয়তন = (1767.15 – 696.9116 ) = 1070.2384 ঘন সে.মি. (প্রায়)

মনে করি, নিরেট গোলকের ব্যাসার্ধ r সে.মি.

নিরেট গোলকের আয়তন = 4/3π × r3 ঘন সে.মি.

যেহেতু ফাঁপা গোলকে ব্যবহৃত লোহা দিয়ে নিরেট গোলকটি তৈরি করা হয়েছে, সেহেতু লোহার আয়তন নিরেট গোলকের আয়তনের সমান।

4/3π × r3 = 1070.2384

বা, r3 = 255.5

বা, r = 6.3454 সে.মি.

নিরেট গোলকটির পৃষ্ঠতলের ক্ষেত্রফল : 4π × (6.3454) 2 = 505.9748 বর্গ সে.মি. (প্রায়)

গ) নিরেট গোলকের ব্যাসার্ধ 6.3454 সে.মি.

নিরেট গোলকের ব্যাস 2 x 6.3454 সে.মি. = 12.6908 সে.মি.

যেহেতু নিরেট গোলকটি ঘনক আকৃতির বাক্সে ঠিকভাবে এঁটে যায়, সেহেতু বাক্সটির দৈর্ঘ্য হবে নিরেট গোলকের ব্যাসের সমান।সুতরাং ঘনক আকৃতির বাক্সের দৈর্ঘ্য = 12.6908 সে.মি.

.: বাক্সটির আয়তন = ( 12.6908 )3 = 2043.9346 ঘন সে.মি. (প্রায়)

নিরেট গোলকের আয়তন = ফাঁপা গোলকে ব্যবহৃত লোহার আয়তন (প্রায়) = 1070.2384 ঘন সে.মি.

বাক্সটির অনধিকৃত অংশের আয়তন = (2043.9346 -1070.2384) = 973.6962 ঘন সে.মি. (প্রায়)

আরও দেখুনঃ

• ভেক্টর রাশির জ্যামিতিক প্রতিরূপ: দিক নির্দেশক রেখাংশ

• স্মল অয়েল সার্কিট ব্রেকার এর সুবিধা ও অসুবিধা