আজকে আমাদের আলোচনার বিষয়ঃ চতুর্ভুজ অঙ্কন। এটি নবম – দশম শ্রেনী গণিতের ব্যবহারিক জ্যামিতি এর অন্তর্গত।

চতুর্ভুজ অঙ্কন
আমরা দেখেছি যে, ত্রিভুজের তিনটি উপাত্ত দেওয়া থাকলে অনেক ক্ষেত্রেই ত্রিভুজটি নির্দিষ্টভাবে আঁকা সম্ভব। কিন্তু চতুর্ভুজের চারটি বাহু দেওয়া থাকলেই একটি নির্দিষ্ট চতুর্ভুজ আঁকা যায় না। নির্দিষ্ট চতুৰ্ভুজ আঁকার জন্য পাঁচটি স্বতন্ত্র উপাত্ত প্রয়োজন হয়। নিম্নে বর্ণিত পাঁচটি উপাত্ত জানা থাকলে, নির্দিষ্ট চতুর্ভুজ আঁকা যায়।
১. চারটি বাহু ও একটি কোণ
২. চারটি বাহু ও একটি কর্ণ
৩. তিনটি বাহু ও দুইটি কর্ণ
৪. তিনটি বাহু ও এদের অন্তর্ভুক্ত দুইটি কোণ
৫. দুইটি বাহু ও তিনটি কোণ।
অষ্টম শ্রেণিতে উল্লেখিত উপাত্ত দিয়ে চতুর্ভুজ অঙ্কন বিষয়ে আলোচনা করা হয়েছে। অঙ্কনের কৌশল লক্ষ করে দেখা যায় কিছু ক্ষেত্রে সরাসরি চতুর্ভুজ আঁকা হয়। আবার কিছু ক্ষেত্রে ত্রিভুজ অঙ্কনের মাধ্যমে চতুর্ভুজ আঁকা হয়। যেহেতু কর্ণ চতুর্ভুজকে দুইটি ত্রিভুজে বিভক্ত করে, সেহেতু উপাত্ত হিসাবে একটি বা দুইটি কর্ণ প্রদত্ত হলে ত্রিভুজ অঙ্কনের মাধ্যমে চতুর্ভুজ আঁকা সম্ভব হয়।
১. চারটি বাহু ও একটি কোণ
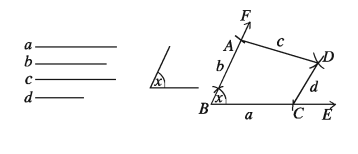
২. চারটি বাহু ও একটি কর্ণ
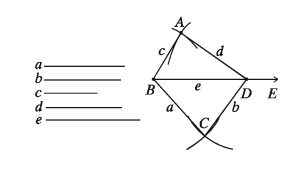
৩. তিনটি বাহু ও দুইটি কর্ণ
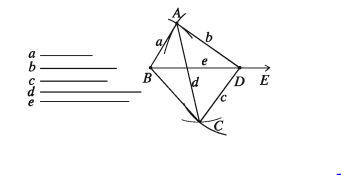
৪. তিনটি বাহু ও এদের অন্তর্ভুক্ত দুইটি কোণ
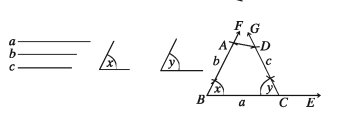
৫. দুইটি বাহু ও তিনটি কোণ।
বিশেষ ধরনের চতুর্ভুজ অঙ্কনের জন্য অনেক সময় এমন উপাত্ত দেওয়া থাকে যা থেকে নির্দিষ্ট চতুর্ভুজ আঁকার জন্য প্রয়োজনীয় পাঁচটি স্বতন্ত্র উপাত্ত পাওয়া যায়। তাহলে ঐ উপাত্তের সাহায্যেও চতুর্ভুজটি আঁকা যায়। যেমন, সামান্তরিকের দুইটি সংলগ্ন বাহু ও এদের অন্তর্ভুক্ত কোণটি দেওয়া থাকলে সামান্তরিকটি আঁকা যায়। এখানে তিনটি মাত্র উপাত্ত দেওয়া আছে। আবার বর্গের মাত্র একটি বাহু দেওয়া থাকলেই বর্গটি আঁকা যায়। কারণ, তাতে পাঁচটি উপাত্ত, যথা: বর্গের চার সমান বাহু ও এক কোণ (সমকোণ নির্দিষ্ট হয়।
সম্পাদ্য ৪.
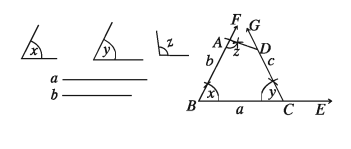
সামান্তরিকের দুইটি কর্ণ ও এদের অন্তর্ভুক্ত একটি কোণ দেওয়া আছে। সামান্তরিকটি আঁকতে হবে।
মনে করি, সামান্তরিকের কর্ণ দুইটি a ও b এবং কর্ণদ্বয়ের অন্তর্ভুক্ত একটি কোণ ∠x দেওয়া আছে। সামান্তরিকটি আঁকতে হবে।
অঙ্কন :
যেকোনো রশ্মি AE থেকে a. এর সমান AC রেখাংশ নিই। AC এর মধ্যবিন্দু O নির্ণয় করি। O বিন্দুতে ∠x এর সমান ∠AOP আঁকি।
OP এর বিপরীত রশ্মি OQ অঙ্কন করি। OP এর বিপরীত রশ্মি OQ অঙ্কন করি। OQ রশ্মিদ্বয় থেকে = 1/2b এর সমান যথাক্রমে OB ও OD রেখাংশদ্বয় নিই। A, B, A, D; C, B ও C, D যোগ করি।
তাহলে, ABCD ই উদ্দিষ্ট সামান্তরিক।
প্রমাণ:
∆AOB ও ∆COD এ OA = OC = 1/2a, OB = OD = 1/2b [অঙ্কনানুসারে]
এবং অন্তর্ভুক্ত ∠AOB = অন্তর্ভুক্ত ∠COD [ বিপ্রতীপ কোণ]
অতএব, ∆AOB = ∆COD
সুতরাং, AB = CD এবং ∠ABO = ∠CDO; কিন্তু কোণ দুইটি একান্তর কোণ।
AB ও CD সমান ও সমান্তরাল।
অনুরূপভাবে, AD ও BC সমান ও সমান্তরাল।
সুতরাং, ABCD একটি সামান্তরিক যার কর্ণদ্বয় AC = AO + OC = 1/2a + 1/2a = a ও BD = BO + OD = 1/2b + 1/2b = b এবং
কর্ণ দুইটির অন্তর্ভুক্ত ∠AOB = ∠a
অতএব, ABCD ই নির্ণেয় সামান্তরিক।
সম্পাদ্য ৫.
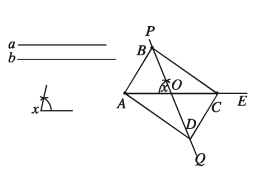
সামান্তরিকের দুইটি কর্ণ ও একটি বাহু দেওয়া আছে। সামান্তরিকটি আঁকতে হবে।
মনে করি সামান্তরিকের দুইটি কর্ণ a ও b এবং একটি বাহু দেওয়া আছে। সামান্তরিকটি আঁকতে হবে।
অঙ্কন:
a ও b কর্ণদ্বয়কে সমান দুইভাগে বিভক্ত করি। যেকোনো রশ্মি AX থেকে c এর সমান AB নিই। A ও B কে কেন্দ্র করে যথাক্রমে a/2 ও b/2 এর সমান ব্যাসার্ধ নিয়ে 2 2 AB এর একই পাশে দুইটি বৃত্তচাপ আঁকি। মনে করি, বৃত্তচাপ দুইটি পরস্পরকে O বিন্দুতে ছেদ করে। A, O ও B, O যোগ করি। AO কে AE বরাবর এবং BO কে BF বরাবর বর্ধিত a করি। OE থেকে a/2 = OC এবং OF থেকে b/2 = OD নিই। A, D, D, C ও B, C যোগ করি।
তাহলে, ABCD ই উদ্দিষ্ট সামান্তরিক।
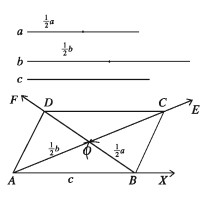
প্রমাণ:
∆AOB ও ∆COD এ
OA = OC = a/2; OB = OD = = b/2 [অঙ্কনানুসারে]
এবং অন্তর্ভুক্ত ∠AOB = অন্তর্ভুক্ত ∠COD [বিপ্রতীপ কোণ]
∆AOB = ∆COD
AB = CD এবং ∠ABO = ∠ODC; কিন্তু কোণ দুইটি একান্তর কোণ।
AB ও CD সমান ও সমান্তরাল।
অনুরূপভাবে, AD ও BC সমান ও সমান্তরাল।
অতএব, ABCD ই নির্ণেয় সামান্তরিক।
উদাহরণ ৩.
ট্রাপিজিয়ামের দুইটি সমান্তরাল বাহু এবং এদের মধ্যে বৃহত্তর বাহু সংলগ্ন দুইটি কোণ দেওয়া আছে। ট্রাপিজিয়ামটি আঁক।
মনে করি, ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয় a এবং b, যেখানে a > b এবং বৃহত্তর বাহু . সংলগ্ন কোণদ্বয় ∠x ও ∠y। ট্রাপিজিয়ামটি আঁকতে হবে।
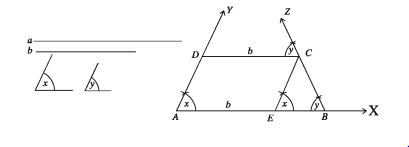
অঙ্কন :
যেকোনো রশ্মি AX থেকে AB = a নিই। AB রেখাংশের A বিন্দুতে ∠x এর সমান ∠BAY এবং B বিন্দুতে ∠y এর সমান ∠ABZ আঁকি।
এবার AB রেখাংশ থেকে AE = b কেটে নিই। E বিন্দুতে EC || AY আঁকি যা BZ রশ্মিতে C বিন্দুতে ছেদ করে। এবার CD || BA আঁকি। CD রেখাংশ AY রশ্মিকে D বিন্দুতে ছেদ করে।
তাহলে, ABCD ই উদ্দিষ্ট ট্রাপিজিয়াম।
প্রমাণ:
অঙ্কনানুসারে, AE || CD এবং AD || EC সুতরাং AECD একটি সামান্তরিক এবং CD = AE = b।
এখন, চতুর্ভুজ ABCD এ AB = a, CD = b, AB || CD এবং ∠BAD = ∠x, ∠ABC = ∠y [অঙ্কন অনুসারে]
অতএব, ABCD ই নির্ণেয় ট্রাপিজিয়াম।
উদাহরণ ৪.
ABC ত্রিভুজের ∠B = 60°, ∠C = 45° এবং পরিসীমা p= 13 সে.মি.।
ক) স্কেল ও কম্পাস দিয়ে ∠B ও ∠C আঁক।
খ) ত্রিভুজটি অঙ্কন কর। (অঙ্কনের চিহ্ন ও বিবরণ আবশ্যক)
গ) একটি রম্বস আঁক যার বাহুর দৈর্ঘ্য এর সমান এবং একটি কোণ ∠B এর সমান। (অঙ্কনের চিহ্ন ও বিবরণ আবশ্যক)
সমাধান :
ক)
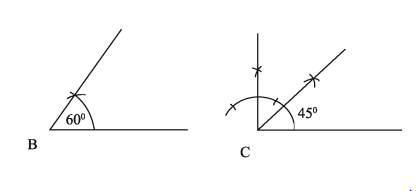
খ)
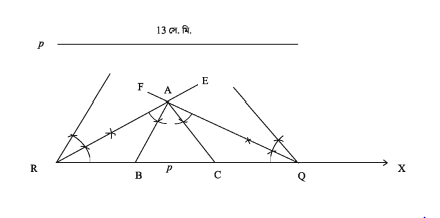
যেকোনো রশ্মি RX থেকে RQ = p কেটে নেই। R বিন্দুতে 1/2∠B এবং Q বিন্দুতে 1/2∠c এর সমান করে যথাক্রমে ∠ERX ও ∠FQR আঁকি। ER ও FQ A বিন্দুতে ছেদ করে। এবার A বিন্দুতে ER এর যে পাশে ∠ERX অবস্থিত সে ই পাশে ∠RAB = 1/2∠B এবং FQ এর যে পাশে ∠FQR অবস্থিত সে ই পাশে ∠QAC = 1/2∠C আঁকি। AB ও AC রেখাংশ, RQ কে যথাক্রমে B C বিন্দুতে ছেদ করে।
ABC উদ্দিষ্ট ত্রিভুজ।
গ) রম্বসের বাহুর দৈর্ঘ্য 1/3p, একটি কোণ ∠B = 60° দেওয়া আছে। রম্বসটি আঁকতে হবে।
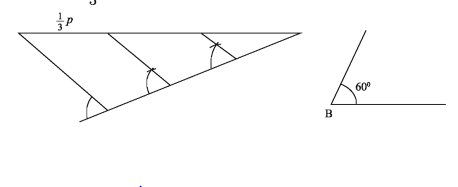
BX যেকোনো রশ্মি থেকে BA = 1/3p কাটি। B বিন্দুতে ∠ABE = 60° আঁকি। BE থেকে BC = AB নেই। আবার A ও C বিন্দুকে কেন্দ্র করে 1/3p এর সমান ব্যাসার্ধ নিয়ে ∠ABC এর অভ্যন্তরে দুইটি বৃত্তচাপ আঁকি। বৃত্তচাপদ্বয় পরস্পর D বিন্দুতে ছেদ করে। A, D, C, D যোগ করি।
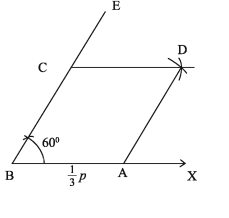
ABCD উদ্দিষ্ট রম্বস।
