আজকে আমাদের আলোচনার বিষয়ঃ চতুর্ভুজ ক্ষেত্রের ক্ষেত্রফল। এটি নবম – দশম শ্রেনী গণিতের পরিমিতি অংশের অন্তর্গত।

চতুর্ভুজ ক্ষেত্রের ক্ষেত্রফল
১. আয়তক্ষেত্রের ক্ষেত্রফল
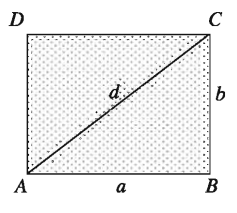
মনে করি, ABCD আয়তক্ষেত্রের দৈর্ঘ্য AB = a, প্রস্থ BC = b এবং কর্ণ AC = d
আমরা জানি, আয়তক্ষেত্রের কর্ণ আয়তক্ষেত্রটিকে সমান দুইটি ত্রিভুজক্ষেত্রে বিভক্ত করে।
আয়তক্ষেত্র ABCD এর ক্ষেত্রফল = 2 × ∆ABC এর ক্ষেত্রফল
= 2 × 1/2 a.b = ab
লক্ষ করি, আয়তক্ষেত্রটির পরিসীমা s = 2 (a + b) এবং ABC ত্রিভুজটি সমকোণী।
AC2 = AB2 + BC2 বা, d2 = a2 + b2
d = √(a2 + b2)
২. বর্গক্ষেত্রের ক্ষেত্রফল :
মনে করি, ABCD বর্গক্ষেত্রের প্রতি বাহুর দৈর্ঘ্য a এবং কর্ণ d
AC কর্ণ বর্গক্ষেত্রক্ষত্রটিকে সমান দুইটি ত্রিভুজক্ষত্রে বিভক্ত করে।
বর্গক্ষেত্র ABCD এর ক্ষেত্রফল = 2 × ∆ABC এর ক্ষেত্রফল
= 2 × 1/2 a.a = a2 = (বাহুর দৈর্ঘ্য) 2
লক্ষ করি, বর্গক্ষেত্রের পরিসীমা s = 4a এবং
কর্ণ d = √(a2 + a2) = √2a2 = √2a

৩. সামান্তরিকক্ষেত্রের ক্ষেত্রফল :
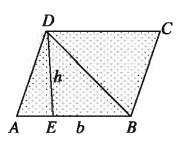
ক) ভূমি ও উচ্চতা দেওয়া আছে:
মনে করি, ABCD সামান্তরিকক্ষেত্রের ভূমি AB b এবং = উচ্চতা DE = h । BD কর্ণ সামান্তরিকক্ষেত্রটিকে সমান দুইটি ত্রিভুজক্ষেত্রে বিভক্ত করে।
সামান্তরিকক্ষেত্র ABCD এর ক্ষেত্রফল
= 2 × ∆ABD এর ক্ষেত্রফল = 2 × 1/2b.h = bh .
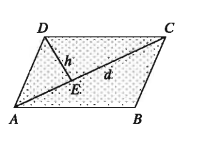
খ) একটি কর্ণের দৈর্ঘ্য এবং ঐ কর্ণের বিপরীত কৌণিক বিন্দু থেকে উক্ত কর্ণের উপর অঙ্কিত লম্বের দৈর্ঘ্য দেওয়া আছে :
মনে করি, ABCD সামান্তরিকের কর্ণ AC = d এবং এর বিপরীত কৌণিক বিন্দু D থেকে AC এর উপর অঙ্কিত লম্ব DE = h। কর্ণ AC সামান্তরিকক্ষেত্রটিকে সমান দুইটি ত্রিভুজক্ষেত্রে বিভক্ত করে।
সামান্তরিকক্ষেত্র ABCD এর ক্ষেত্রফল 1 = 1/2 × ∆ACD এর ক্ষেত্রফল = 2 × 1/2d.h = dh
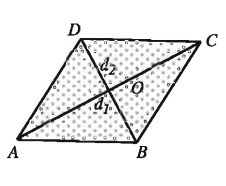
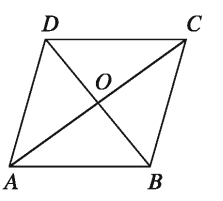
৪. রম্বসের ক্ষেত্রফল:
রম্বসের দুইটি কর্ণ দেওয়া আছে। মনে করি, ABCD রম্বসের কর্ণ AC = d1, কর্ণ BD = d2 এবং কর্ণদ্বয় পরস্পর O বিন্দুতে ছেদ করে।
কর্ণ AC রম্বসক্ষেত্রটিকে সমান দুইটি ত্রিভুজক্ষেত্রে বিভক্ত করে। আমরা জানি, রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে।
∆ACD এর উচ্চতা = d2/2
রম্বস ABCD এর ক্ষেত্রফল
= 2 × ∆ACD এর ক্ষেত্রফল =2 × 1/2d1.d2/2 = 1/2d1d2
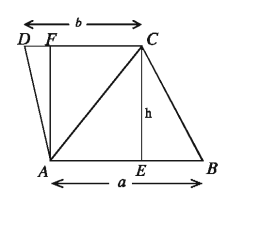
৫. ট্রাপিজিয়ামক্ষেত্রের ক্ষেত্রফল :
ট্রাপিজিয়ামক্ষেত্রের সমান্তরাল দুইটি বাহু এবং এদের মধ্যবর্তী লম্ব দূরত্ব দেওয়া আছে। মনে করি, ABCD ট্রাপিজিয়ামক্ষেত্রের সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্য যথাক্রমে AB = a একক, CD b একক এবং এদের মধ্যবর্তী দূরত্ব CE = AF = h। কর্ণ AC ট্রাপিজিয়াম ABCD ক্ষেত্রটিকে ∆ABC ও ∆ACD ক্ষেত্রে বিভক্ত করে।
ট্রাপিজিয়াম ABCD এর ক্ষেত্রফল
= ∆ABC এর ক্ষেত্রফল + ∆ACD এর ক্ষেত্রফল
= 1/2AB × CE + 1/2CD × AF
= 1/2 ah + 1/2bh = h(a + b)/2
উদাহরণ ৮.
একটি আয়তাকার ঘরের দৈর্ঘ্য প্রস্থের 3/2 গুণ। এর ক্ষেত্রফল 384 বর্গমিটার হলে, 2 পরিসীমা ও কর্ণের দৈর্ঘ্য নির্ণয় কর।
সমাধান:
মনে করি, আয়তাকার ঘরের প্রস্থ x মিটার।
ঘরের দৈর্ঘ্য 3/2x এবং ক্ষেত্রফল = 3/2 × x = 3/2×2
প্রশ্নানুসারে, 3/2×2 = 384
বা, 3×2 = 768
বা, x2 = 256
x = 16 মিটার।
আয়তাকার ঘরের দৈর্ঘ্য = 3/2 × 16 = 24 মিটার এবং প্রস্থ = 16 মিটার।
ঘরটির পরিসীমা = 2 (24 + 16) মিটার ৪০ মিটার এবং কর্ণের দৈর্ঘ্য √(242 + 162) মিটার = √832 মিটার = 28.84 মিটার (প্রায়)
নির্ণেয় পরিসীমা 80 মিটার এবং কর্ণের দৈর্ঘ্য 28.84 মিটার (প্রায়)
উদাহরণ ৯.
একটি আয়তক্ষেত্রের ক্ষেত্রফল 2000 বর্গমিটার। যদি এর দৈর্ঘ্য 10 মিটার কম হত তাহলে এটি একটি বর্গক্ষেত্র হত। আয়তক্ষেত্রটির দৈর্ঘ্য ও প্রস্থ নির্ণয় কর।
সমাধান:
মনে করি, আয়তক্ষেত্রটির দৈর্ঘ্য x মিটার এবং প্রস্থ y মিটার।
আয়তক্ষেত্রটির ক্ষেত্রফল = xy বর্গমিটার।
প্রশ্নানুসারে, xy = 2000 ( 1 ) এবং x – 10 = y ….( 2 )
সমীকরণ (1) এ y = x – 10 বসিয়ে পাই
x (x – 10 ) = 2000
x2 – 10x – 2000 = 0
বা, x2 – 50x + 40x – 2000 = 0
বা, (x – 50 ) ( x + 40 ) = 0
x= 50 অথবা x = -40
কিন্তু দৈর্ঘ্য ঋণাত্মক হতে পারে না।
:. x = 50
এখন, সমীকরণ (2) এ x এর মান বসিয়ে পাই, y = 50 – 10 = 40
আয়তক্ষেত্রটির দৈর্ঘ্য 50 মিটার এবং প্রস্থ 40 মিটার।
উদাহরণ ১০.
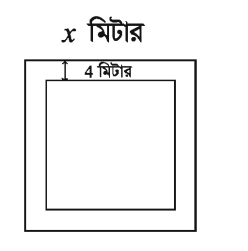
বর্গাকার একটি মাঠের ভিতরে চারদিকে 4 মিটার চওড়া একটি রাস্তা আছে। যদি রাস্তার ক্ষেত্রফল 1 হেক্টর হয়, তবে রাস্তা বাদে মাঠের ভিতরের ক্ষেত্রফল নির্ণয় কর।
সমাধান:
মনে করি, বর্গাকার মাঠের দৈর্ঘ্য x মিটার।
এর ক্ষেত্রফল x2 বর্গমিটার।
মাঠের ভিতরে চারদিকে 4 মিটার চওড়া একটি রাস্তা আছে।
রাস্তা বাদে বর্গাকার মাঠের দৈর্ঘ্য = (x – 2 x 4 ) বা, (x – 8 ) মিটার
রাস্তা বাদে বর্গাকার মাঠের ক্ষেত্রফল = ( x – 8)2 বর্গমিটার
সুতরাং রাস্তার ক্ষেত্রফল = x2 – (x – 8 ) 2 বর্গমিটার
আমরা জানি, 1 হেক্টর = 10000 বর্গমিটার
প্রশ্নানুসারে, x2 – (x – 8 ) 2 = 10000
বা, x2 – x2 + 16x – 64 = 10000
বা, 16x = 10064
x = 629
রাস্তা বাদে বর্গাকার মাঠের ক্ষেত্রফল
= ( 629 – 8 ) 2 বর্গমিটার
= 385641 বর্গমিটার
= 38.56 হেক্টর (প্রায়)
নির্ণেয় ক্ষেত্রফল = 38.56 হেক্টর (প্রায়)।
উদাহরণ ১১.
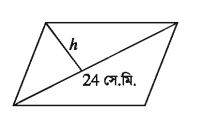
একটি সামান্তরিকক্ষেত্রের ক্ষেত্রফল 120 বর্গ সে.মি. এবং একটি কর্ণ 24 সে.মি.।
সমাধান:
মনে করি, সামান্তরিকক্ষেত্রের একটি কর্ণ d = 24 সে. মি. এবং এর বিপরীত কৌণিক বিন্দু থেকে কর্ণের উপর অঙ্কিত লম্বের দৈর্ঘ্য h সে.মি.।
সামান্তরিকক্ষেত্রটির ক্ষেত্রফল = dh বর্গ সে.মি.
প্রশানুসারে, dh = 120
বা, h = 120/d = 120/24 = 5
নির্ণেয় লম্বের দৈর্ঘ্য 5 সে.মি.।
উদাহরণ ১২.
একটি সামান্তরিকের বাহুর দৈর্ঘ্য 12 মিটার ও ৪ মিটার এবং ক্ষুদ্রতম কর্ণটি 10 মিটার হলে, অপর কর্ণটির দৈর্ঘ্য নির্ণয় কর।
সমাধান :
মনে করি, ABCD সামান্তরিকের AB = a = 12 মিটার, AD = c = = ৪ মিটার এবং কর্ণ BD = b = 10 মিটার। D ও C থেকে AB এর উপর এবং AB এর বর্ধিতাংশের উপর DF ও CE লম্ব টানি। A, C ও B, D যোগ করি।
∆ABD এর অর্ধপরিসীমা s = (12 + 10 +8)/2 মিটার = 15 মিটার
∆ABD এর ক্ষেত্রফল = √{s ( s – a) ( s – b) (s – c)} =√{ 15 ( 15 – 12 ) ( 15 – 10 ) (15 – 8 )} বর্গমিটার
=√(15 x 3 x 5 x 7 )বর্গমিটার = √1575 বর্গমিটার = 39.68 বর্গমিটার (প্রায়)
আবার, ∆ ক্ষেত্র ABD এর ক্ষেত্রফল = 1/2AB × DF
বা, 39.68 = 1/2 × 12 × DF
বা, 6DF = 39.68. DF = 6.61 (প্রায়)
এখন, বা, BCE সমকোণী ।
.: BE2 = BC2 – CE2 = AD2 – DF2 = 82 – (6.61 ) 2 = 20.31
BE = 4.5 (প্রায়)
অতএব, AE = AB + BE = 12 + 4.5 = 16.5 (প্রায়)
∆ACE সমকোণী থেকে পাই
AC2 = AE2 + CE 2 = ( 16.5 ) 2 + (6.61 ) 2 = 315.94
AC = 17.77 (প্রায়)
নির্ণেয় কর্ণের দৈর্ঘ্য 17.77 মিটার (প্রায়)

উদাহরণ ১৩.
একটি রম্বসের একটি কর্ণ 10 মিটার এবং ক্ষেত্রফল 120 বর্গমিটার হলে, অপর কর্ণ এবং পরিসীমা নির্ণয় কর।
সমাধান :
মনে করি, ABCD রম্বসের কর্ণ BD = d1 = 10 মিটার এবং অপর কর্ণ d2 মিটার ।
রম্বসটির ক্ষেত্রফল = 1/2d1d2 বর্গমিটার
প্রশ্নানুসারে, 1/2d1d2 = 120
বা, d2 = (120 x 2)/ 10 = 24 মিটার।
আমরা জানি, রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে।
..OD = OB = 10/2 মিটার =5 মিটার এবং OA = OC = 24/2 মিটার = 12 মিটার
∆AOD সমকোণী ত্রিভুজে
AD2 = OA 2 + OD2 = 122 + 52
AD = 13
রম্বসের প্রতি বাহুর দৈর্ঘ্য 13 মিটার। রম্বসের পরিসীমা = 4 × 13 মিটার = 52 মিটার
নির্ণেয় কর্ণের দৈর্ঘ্য 24 মিটার এবং পরিসীমা 52 মিটার।
উদাহরণ ১৪.
একটি ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্য যথক্রমে 91 সে.মি. ও 51 সে.মি. এবং অপর বাহু দুইটির দৈর্ঘ্য যথাক্রমে 37 সে.মি. ও 13 সে.মি.। ট্রাপিজিয়ামটির ক্ষেত্রফল নির্ণয় কর।
সমাধান :
মনে করি, ABCD ট্রাপিজিয়ামের AB = 91 সে.মি. CD = 51 সে.মি. থেকে। D ও C থেকে AB এর উপর যথাক্রমে DE ও CF লম্ব টানি।
CDEF একটি আয়তক্ষেত্র।
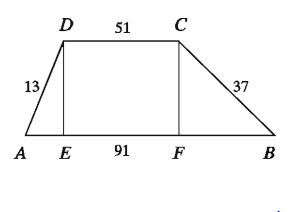
EF = CD = 51 সে.মি.।
ধরি, AE = x এবং DE = CF = h
BF = AB – AF = 91 – (AE + EF) = 91 – ( x + 51 ) = 40 – x
সমকোণী ∆ADE থেকে পাই,
AE2 + DE2 = AD2 বা, x2 + h2 = 132 বা, x2 + h2 = 169 … (1)
আবার সমকোণী ত্রিভুজ BCF এর ক্ষেত্রে
BF2 + CF2 = BC2
বা, ( 40 – x ) 2 + h2 = 372
বা, 1600 – 80x + x2+ h² = 1369
বা, 1600 – 80x + 169 = 1369 [(1) এর সাহায্যে]
বা, 1600 + 169–1369 = 80x
বা, 80x = 400
x = 5
সমীকরণ (1) এ x এর মান বসিয়ে পাই,
52+h2 169
বা, h² = 169 – 25 = 144
h = 12
ট্রাপিজিয়াম ABCD এর ক্ষেত্রফল = 1/2(AB+ CD). h
= 1/2(91 + 51 ) x 12 বর্গ সে.মি. = 71 x 12 বর্গ সে.মি. = 852 বর্গ সে.মি.
নির্ণেয় ক্ষেত্রফল 852 বর্গ সে.মি.।