চতুর্ভুজ ক্ষেত্রের ক্ষেত্রফল

আজকে আমাদের আলোচনার বিষয়ঃ চতুর্ভুজ ক্ষেত্রের ক্ষেত্রফল। এটি অষ্টম শ্রেনী গণিতের চতুর্ভুজ এর অন্তর্গত।

 

 

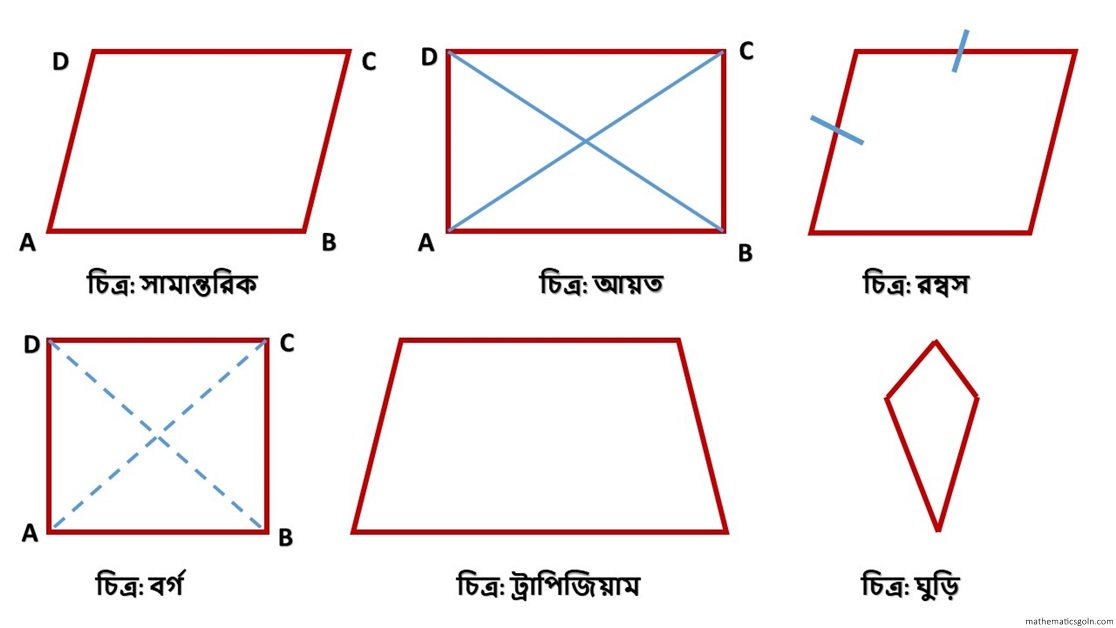
চতুর্ভুজ ক্ষেত্রের ক্ষেত্রফল

চারটি রেখাংশ দ্বারা আবদ্ধ চিত্র একটি চতুর্ভুজ । চিত্র দ্বারা আবদ্ধ ক্ষেত্রটি একটি চতুর্ভুজক্ষেত্র ।

চতুর্ভুজের চারটি বাহু আছে । যে চারটি রেখাংশ দ্বারা ক্ষেত্রটি আবদ্ধ হয়, এ চারটি রেখাংশই চতুর্ভুজের বাহু ।

A, B, C ও D বিন্দু চারটির যেকোনো তিনটি সমরেখ নয়। AB, BC, CD ও DA রেখাংশ চারটি সংযোগে ABCD চতুর্ভুজ গঠিত হয়েছে। AB, BC, CD ও DA চতুর্ভুজটির চারটি বাহু । A, B, C ও D চারটি কৌণিক বিন্দু বা শীর্ষবিন্দু। ∠ABC, ∠BCD, ∠CDA ও ∠DAB চতুর্ভুজের চারটি কোণ ।

একটি চতুর্ভুজের একটি কর্ণ দ্বারা চতুর্ভুজক্ষেত্রটি দুইটি ত্রিভুজক্ষেত্রে বিভক্ত হয় । অতএব, চতুর্ভুজক্ষেত্রের ক্ষেত্রফল ত্রিভুজদ্বয়ের ক্ষেত্রফলের যোগফলের সমান । পূর্ববর্তী শ্রেণিতে আমরা বর্গক্ষেত্র ও আয়তক্ষেত্রের ক্ষেত্রফল নির্ণয় করতে শিখেছি । আবার আয়ত ও সামান্তরিকের ভূমি ও উচ্চতা একই হলেও উল্লিখিত ক্ষেত্রদ্বয়ের ক্ষেত্রফল সমান । নিচে রম্বস ও ট্রাপিজিয়ামক্ষেত্রের ক্ষেত্রফল নির্ণয়কৌশল নিয়ে আলোচনা করা হবে ।

 

 

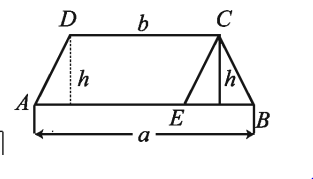
(ক) ট্রাপিজিয়ামক্ষেত্রের ক্ষেত্রফল

ABCD একটি ট্রাপিজিয়াম যেখানে AB ॥ CD, AB=a, CD=b এবং AB ও CD এর লম্ব দূরত্ব =h C বিন্দু দিয়ে DA।। CE আঁকি ।

.: AECD একটি সামান্তরিক। চিত্র থেকে

ABCD ট্রাপিজিয়ামক্ষেত্রের ক্ষেত্রফল = AECD সামান্তরিকক্ষেত্রের ক্ষেত্রফল + CEB ত্রিভুজক্ষেত্রের
ক্ষেত্রফল

= b x h+1/2(a−b) x h

= 1/2(a + b) x h

ট্রাপিজিয়াম ক্ষেত্রের ক্ষেত্রফল = সমান্তরাল বাহুদ্বয়ের সমষ্টির গড় × উচ্চতা

 

 

রম্বসক্ষেত্রের ক্ষেত্রফল

রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে। তাই রম্বসের কর্ণদ্বয়ের দৈর্ঘ্য জানা থাকলে সহজেই রম্বসক্ষেত্রের ক্ষেত্রফল নির্ণয় করা যায় ।

মনে করি, ABCD রম্বসের AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করে । কর্ণদ্বয়ের দৈর্ঘ্যকে যথাক্রমে a ও b দ্বারা নির্দেশ করি ।

রম্বসক্ষেত্রের ক্ষেত্রফল = DAC ত্রিভুজক্ষেত্রের ক্ষেত্রফল + BAC ত্রিভুজক্ষেত্রের ক্ষেত্রফল

= 1/2. a x 1/2b + 1/2 a x -1/2b

= 1/2 a x b

রম্বসক্ষেত্রের ক্ষেত্রফল = কর্ণদ্বয়ের গুণফলের অর্ধেক