আজকে আমাদের আলোচনার বিষয়ঃ চতুর্ভুজ সংক্রান্ত উপপাদ্য । এটি অষ্টম শ্রেনী গণিতের চতুর্ভুজ এর অন্তর্গত।

চতুর্ভুজ সংক্রান্ত উপপাদ্য
বিভিন্ন প্রকারের চতুর্ভুজের কিছু সাধারণ ধর্ম রয়েছে। এ ধর্মগুলো উপপাদ্য আকারে প্রমাণ করা হলো ।
উপপাদ্য ১
চতুর্ভুজের চারটি কোণের সমষ্টি চার সমকোণ ।
বিশেষ নির্বচন
মনে করি, ABCD একটি চতুর্ভূজ ।
প্রমাণ করতে হবে যে, ZA+ 2B + ZC + D = 4 সমকোণ।
অঙ্কন:
A ও C যোগ করি। AC কর্ণটি চতুর্ভুজটিকে ABC ও AADC দুইটি ত্রিভুজে বিভক্ত করেছে।

প্রমাণঃ
| ধাপ | যথার্থতা |
| (১) ∆ABC ∠BAC + ∠ACB + ∠B = 2 সমকোণ ।
(২) অনুরূপভাবে, ∆DAC এ ∠DAC + ∠ACD +∠D = 2 সমকোণ । (৩) অতএব, ∠DAC + ∠ACD + ∠D + ∠BAC + ∠ACB + ∠B = ( 2 + 2 ) সমকোণ (8) ∠DAC + ∠BAC = ∠A এবং ∠ACD+∠ACB=∠C সুতরাং, ∠A+ ∠B + ∠C + ∠D = 4 সমকোণ (প্রমাণিত) |
[ ত্রিভুজের তিন কোণের সমষ্টি 2 সমকোণ ]
[ ত্রিভুজের তিন কোণের সমষ্টি 2 সমকোণ ] [ (১) ও (২) থেকে ] [সন্নিহিত কোণের যোগফল । [সন্নিহিত কোণের যোগফল ] [ (৩) থেকে ] |
উপপাদ্য ২
সামান্তরিকের বিপরীত বাহু ও কোণগুলো পরস্পর সমান ।
বিশেষ নির্বচন :
মনে করি, ABCD একটি সামান্তরিক এবং AC ও BD তার দুইটি কর্ণ ।
প্রমাণ করতে হবে যে,
(ক) AB বাহু = CD বাহু, AD বাহু = BC বাহু
(খ) ∠BAD = ∠BCD, ∠ABC = ∠ADC

| ধাপ | যথার্থতা |
| (১) AB || DC এবং AC তাদের ছেদক, সুতরাং ∠BAC = ∠ACD
(২) আবার, BC | AD এবং AC তাদের ছেদক, সুতরাং ∠ACB = ∠DAC (৩) এখন ∆ABC ও ∆ADC এ ∠BAC = ∠ACD, ∠ACB = ∠DAC এবং AC বাহু সাধারণ । :. ∆ABC ≌ ∆ADC অতএব, AB = CD, BC = AD ও ∠ABC = ∠ADC অনুরূপভাবে, প্রমাণ করা যায় যে, ∆BAD ≌ ∆BCD সুতরাং, ∠BAD = ∠BCD [প্রমাণিত] |
[একান্তর কোণ সমান ]
[একান্তর কোণ সমান ] [ ত্রিভুজের কোণ-বাহু-কোণ উপপাদ্য ] |
উপপাদ্য ৩
সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে ।
বিশেষ নির্বচন :
মনে করি, ABCD সামান্তরিকের AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করে ।
প্রমাণ করতে হবে যে, AO = CO, BO = DO

প্ৰমাণ :
| ধাপ | যথার্থতা |
| (১) AB ও DC রেখাদ্বয় সমান্তরাল এবং AC এদের ছেদক । অতএব, ∠BAC = একান্তর ∠ACD
(২) AB ও DC রেখাদ্বয় সমান্তরাল এবং BD এদের ছেদক। সুতরাং, ∠BDC = একান্তর ∠ABD (৩) এখন, ∆AOB ও ∆COD এ সুতরাং, ∆AOB ≌ ∆COD অতএব, AO = CO এবং BO = DO (প্রমাণিত) |
[একান্তর কোণ সমান]
[একান্তর কোণ সমান ∠BAC = ∠ACD; ∠BDC = ∠ABD [ ত্রিভুজের কোণ-বাহু-কোণ উপপাদ্য] |
উপপাদ্য ৪
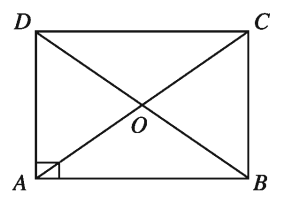
আয়তের কর্ণদ্বয় সমান ও পরস্পরকে সমদ্বিখণ্ডিত করে ।
বিশেষ নির্বচন :
মনে করি, ABCD আয়তের AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করে ।
প্রমাণ করতে হবে যে,
(i) AC = BD
(ii) AO = CO, BO = DO
প্ৰমাণ :
| ধাপ | যথার্থতা |
| (১) আয়ত একটি সামান্তরিক । সুতরাং, AO=CO, BO=DO(২) এখন ∆ABD ও ∆ACD এ AB = DC এবং AD = ADঅন্তর্ভূক্ত ∠DAB = অন্তর্ভূক্ত ∠ADCসুতরাং, ∆ABD = ∆ACDঅতএব, AC = BD (প্রমাণিত) |
[সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে]
[ সামান্তরিকের বিপরীত বাহু পরস্পর সমান [ সাধারণ বাহু ] প্রত্যেকে সমকোণ |
উপপাদ্য ৫
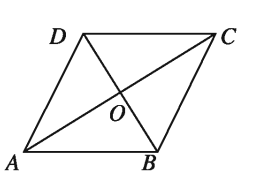
রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে।
বিশেষ নির্বচন :
মনে করি, ABCD রম্বসের AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করে ।
প্রমাণ করতে হবে যে,
(i) ∠AOB = ∠BOC = ∠COD = ∠DOA = 1 সমকোণ
(ii) AO = CO, BO = DO
প্ৰমাণ :
| ধাপ | যথার্থতা |
| (১) রম্বস একটি সামান্তরিক । সুতরাং, AO=CO, BO=DO
(২) এখন ∆AOB ও ∆BOC এ AB = BC AO=CO এবং OB = OB অতএব, ∆AOB = ∆BOC |
[ সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে ]
[ রম্বসের বাহুগুলো সমান ] [ (১) থেকে ] [ সাধারণ বাহু ] [ ত্রিভুজের বাহু-বাহু-বাহু উপপাদ্য ] |
সুতরাং ∠AOB = ∠BOC.
∠AOB + ∠BOC = 1 সরলকোণ = 2 সমকোণ ।
∠AOB = ∠BOC =1 সমকোণ ।
অনুরূপভাবে, প্রমাণ করা যায় যে,
∠COD = ∠DOA = 1 সমকোণ (প্রমাণিত)
