সমতলীয় জ্যামিতিক চিত্র বৃত্ত

আজকে আমাদের  আলোচনার বিষয়ঃ সমতলীয় জ্যামিতিক চিত্র বৃত্ত। এটি নবম – দশম শ্রেনী গণিতের বৃত্ত এর অন্তর্গত।

 

 

সমতলীয় জ্যামিতিক চিত্র বৃত্ত

বৃত্ত একটি সমতলীয় জ্যামিতিক চিত্র যার বিন্দুগুলো কোনো নির্দিষ্ট বিন্দু থেকে সমদূরত্বে অবস্থিত। নির্দিষ্ট বিন্দুটি বৃত্তের কেন্দ্র। নির্দিষ্ট বিন্দু থেকে সমদূরত্ব বজায় রেখে কোনো বিন্দু যে আবদ্ধ পথ চিত্রিত করে তাই বৃত্ত। কেন্দ্র হতে বৃত্তস্থ কোনো বিন্দুর দূরত্বকে ব্যাসার্ধ বলে।

মনে করি, O সমতলের কোনো নির্দিষ্ট বিন্দু এবং , নির্দিষ্ট পরিমাপ। সমতলস্থ যে সকল বিন্দু O থেকে দূরত্বে অবস্থিত, এদের সেট বৃত্ত, যার কেন্দ্র O ও ব্যাসার্ধ । চিত্রে O বৃত্তের কেন্দ্র, A, B ও C বৃত্তস্থ বিন্দু। OA, OB ও OC এর প্রত্যেকটি বৃত্তটির ব্যাসার্ধ।

সমতলস্থ কতিপয় বিন্দুকে সমবৃত্ত বিন্দু বলা হয় যদি বিন্দুগুলো দিয়ে একটি বৃত্ত যায় অর্থাৎ, এমন একটি বৃত্ত থাকে যাতে বিন্দুগুলো অবস্থিত হয়। উপরের চিত্রে A, B ও C সমবৃত্ত বিন্দু।

বৃত্তের অভ্যন্তর ও বহির্ভাগ (Interior and exterior of a circle)

যদি কোনো বৃত্তের কেন্দ্র O এবং ব্যাসার্ধ, হয় তবে O থেকে সমতলের যে সকল বিন্দুর দূরত্ব এর চেয়ে কম এদের সেটকে বৃত্তটির অভ্যন্তর এবং O থেকে সমতলের যে সকল বিন্দুর দূরত্ব r এর  চেয়ে বেশি এদের সেটকে বৃত্তটির বহির্ভাগ বলা হয। বৃত্তের অভ্যন্তরস্থ দুইটি বিন্দুর সংযোজক রেখাংশ সম্পূর্ণভাবে বৃত্তের অভ্যন্তরেই থাকে।

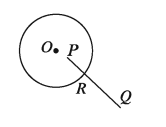
কোনো বৃত্তের অভ্যন্তরস্থ একটি বিন্দু ও বহিঃস্থ একটি বিন্দুর সংযোজক রেখাংশ বৃত্তটিকে একটি ও কেবল একটি বিন্দুতে ছেদ করে। চিত্রে, P বৃত্তের অভ্যন্তরস্থ একটি বিন্দু এবং Q বৃত্তের বহিঃস্থ একটি বিন্দু। PQ রেখাংশ বৃত্তটিকে কেবল R. বিন্দুতে ছেদ করে।

 

 

 

বৃত্তের জ্যা ও ব্যাস (Chord and diameter of a circle)

বৃত্তের দুইটি ভিন্ন বিন্দুর সংযোজক রেখাংশ বৃত্তটির একটি জ্যা। বৃত্তের কোনো জ্যা যদি কেন্দ্র দিয়ে যায় তবে জ্যাটিকে বৃত্তের ব্যাস বলা হয়। অর্থাৎ বৃত্তের কেন্দ্রগামী যেকোনো জ্যা হলো ব্যাস। চিত্রে, AB ও AC বৃত্তটির দুইটি জ্যা এবং বৃত্তটির কেন্দ্র O। এদের মধ্যে AC জ্যাটি ব্যাস; কারণ জ্যাটি বৃত্তটির কেন্দ্রগামী। OA ও OC বৃত্তের দুইটি ব্যাসার্ধ সুতরাং, বৃত্তের কেন্দ্র প্রত্যেক ব্যাসের মধ্যবিন্দু। অতএব প্রত্যেক ব্যাসের দৈর্ঘ্য 2r, যেখানে । বৃত্তটির ব্যাসার্ধ।

 

 

উপপাদ্য ১৭.

বৃত্তের কেন্দ্র ও ব্যাস ভিন্ন কোনো জ্যা এর মধ্যবিন্দুর সংযোজক রেখাংশ ঐ জ্যা এর ওপর লম্ব।

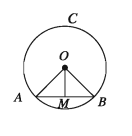
মনে করি, O কেন্দ্রবিশিষ্ট ABC বৃত্তে ব্যাস নয় এমন একটি জ্যা AB এবং এই জ্যা এর মধ্য বিন্দু MO, M যোগ করি। প্রমাণ করতে হবে যে, OM রেখাংশ AB জ্যা এর উপর লম্ব।

অঙ্কন :

O, A এবং O, B যোগ করি।

 

 

প্ৰমাণ:

ধাপ ১.

∆OAM এবং ∆OBM এ

AM = BM [ M, AB এর মধ্যবিন্দু]

OA = OB [:: উভয়ে একই বৃত্তের ব্যাসার্ধ ]

এবং OM = OM [সাধারণ বাহু]

সুতরাং, ∆OAM = ∆OBM [বাহু-বাহু-বাহু উপপাদ্য ]

∠OMA = ∠OMB

 

 

ধাপ ২.

যেহেতু কোণদ্বয় রৈখিক যুগল কোণ এবং এদের পরিমাপ সমান সুতরাং, ZOMA = LOMB = এক সমকোণ । অতএব, OM | AB। (প্রমাণিত)

অনুসিদ্ধান্ত ১.

বৃত্তের যেকোনো জ্যা এর লম্বদ্বিখণ্ডক কেন্দ্রগামী।

অনুসিদ্ধান্ত ২.

যেকোনো সরলরেখা একটি বৃত্তকে দুইয়ের অধিক বিন্দুতে ছেদ করতে পারে না।

উপপাদ্য ১৮.

বৃত্তের সকল সমান জ্যা কেন্দ্র থেকে সমদূরবর্তী।

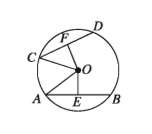
মনে করি, O বৃত্তের কেন্দ্র এবং AB ও CD বৃত্তের দুইটি সমান জ্যা। প্রমাণ করতে হবে যে, O থেকে AB এবং CD জ্যাদ্বয় সমদূরবর্তী।

অঙ্কন :

O থেকে AB এবং CD জ্যা এর উপর যথাক্রমে OE এবং OF লম্ব রেখাংশ আঁকি। O, A এবং O, C যোগ করি।

 

 

প্ৰমাণ:

ধাপ ১.

OE ⊥ AB এবং OF ⊥ CD

সুতরাং, AE = BE এবং CF = DF  [:: কেন্দ্র থেকে ব্যাস ভিন্ন যেকোনো জ্যা এর উপর অঙ্কিত লম্ব জ্যাকে সমদ্বিখণ্ডিত করে ]

AE = 1/2 AB এবং CF = 1/2 CD

ধাপ ২.

কিন্তু AB = CD [ধরে নেয়া]

AE = CF

ধাপ ৩.

এখন ∆OAE এবং ∆OCF সমকোণী ত্রিভুজদ্বয়ের মধ্যে

অতিভুজ OA = অতিভুজ OC [উভয়ে একই বৃত্তের ব্যাসার্ধ]

এবং

AE = CF [ধাপ ২]

∆OAE ≌ ∆OCF [সমকোণী ত্রিভুজের অতিভুজ-বাহু সর্বসমতা উপপাদ্য]

OE = OF

ধাপ ৪.

কিন্তু OE এবং OF কেন্দ্র O থেকে যথাক্রমে AB জ্যা এবং CD জ্যা এর দূরত্ব। সুতরাং, AB এবং CD জ্যাদ্বয় বৃত্তের কেন্দ্র থেকে সমদূরবর্তী। (প্রমাণিত)

 

উপপাদ্য ১৯.

বৃত্তের কেন্দ্র থেকে সমদূরবর্তী সকল জ্যা পরস্পর সমান।

মনে করি, O বৃত্তের কেন্দ্র এবং AB ও CD দুইটি জ্যা। O থেকে AB ও CD এর উপর যথাক্রমে OE ও OF লম্ব। তাহলে OE ও OF কেন্দ্র থেকে যথাক্রমে AB ও CD জ্যা এর দূরত্ব নির্দেশ করে। OE = OF হলে

প্রমাণ করতে হবে যে, AB = CD

অঙ্কন:

O, A ও O, C যোগ করি।

 

 

প্ৰমাণ:

ধাপ ১.

যেহেতু OE ⊥ AB ও OF ⊥ CD

সুতরাং, ∠OEA = ∠OFC = এক সমকোণ।

ধাপ ২.

এখন, ∆OAE এবং ∆OCF সমকোণী ত্রিভুজদ্বয়ের মধ্যে

অতিভুজ OA = অতিভুজ OC [উভয়ে একই বৃত্তের ব্যাসার্ধ ]

এবং

OE = OF [ধরে নেয়া]

∆OAE = ∆OCF [সমকোণী ত্রিভুজের অতিভুজ-বাহু সর্বসমতা উপপাদ্য]

AE = CF

ধাপ ৩.

AE = 1/2AB এবং CF = 1/2CD  [:: কেন্দ্র থেকে ব্যাস ভিন্ন যেকোনো জ্যা এর উপর অঙ্কিত লম্ব জ্যাকে সমদ্বিখণ্ডিত করে]

ধাপ ৪.

সুতরাং 1/2AB = 1/2CD

অর্থাৎ, AB = CD। (প্রমাণিত)

অনুসিদ্ধান্ত ৩.

বৃত্তের ব্যাসই বৃহত্তম জ্যা।