আজকে আমরা জ্যামিতির ত্রিভুজ অঙ্কন নিয়ে আলোচনা করবো। এটি নবম – দশম শ্রেনী গণিতের ব্যবহারিক জ্যামিতি এর অন্তর্গত।

জ্যামিতির ত্রিভুজ অঙ্কন
প্রত্যেক ত্রিভুজের তিনটি বাহু ও তিনটি কোণ রয়েছে। তবে কোনো ত্রিভুজের আকার ও আকৃতি নির্দিষ্ট করার জন্য সবগুলো বাহু ও কোণের প্রয়োজন হয় না। যেমন, ত্রিভুজের তিন কোণের সমষ্টি দুই সমকোণ বলে এর যেকোনো দুইটি কোণের মান দেওয়া থাকলে তৃতীয় কোণটির মান বের করা যায়।
আবার, ত্রিভুজের সর্বসমতা সংক্রান্ত উপপাদ্যগুলো থেকে দেখা যায় যে, কোনো ত্রিভুজের তিনটি বাহু ও তিনটি কোণ অর্থাৎ ছয়টির মধ্যে কেবলমাত্র নিম্নলিখিত তিনটি অপর এক ত্রিভুজের অনুরূপ তিনটি অংশের সমান হলেই ত্রিভুজ দুইটি সর্বসম হয়। অর্থাৎ, এ তিনটি অংশ দ্বারা নির্দিষ্ট আকারের অনন্য ত্রিভুজ আঁকা যায়। সপ্তম শ্রেণিতে আমরা নিম্নবর্ণিত উপাত্ত থেকে ত্রিভুজ আঁকতে শিখেছি।
১ . তিনটি বাহু
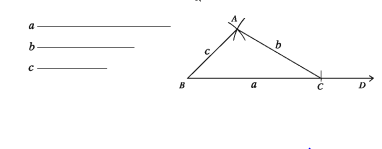
২. দুইটি বাহু ও এদের অন্তর্ভুক্ত কোণ

৩. দুইটি কোণ ও এদের সংলগ্ন বাহু

৪. দুইটি কোণ একটির বিপরীত বাহু

৫. দুইটি বাহু ও এদের একটির বিপরীত কোণ
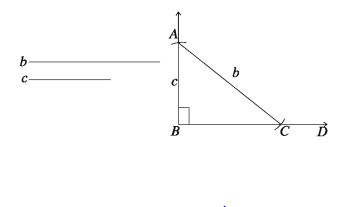
৬. সমকোণী ত্রিভুজের অতিভুজ ও অপর একটি বাহু
লক্ষণীয় যে, উপরের প্রত্যেক ক্ষেত্রে ত্রিভুজের তিনটি অংশ নির্দিষ্ট করা হয়েছে। কিন্তু যেকোনো তিনটি অংশ নির্দিষ্ট করলেই ত্রিভুজটি নির্দিষ্ট হয় না। যেমন, ত্রিভুজের তিনটি কোণ দেওয়া থাকলে বিভিন্ন আকারের অসংখ্য ত্রিভুজ আঁকা যায় (যাদের সদৃশ ত্রিভুজ বলা হয়)।

অনেক সময় ত্রিভুজ আঁকার জন্য এমন তিনটি উপাত্ত দেওয়া থাকে, যাদের সাহায্যে বিভিন্ন অঙ্কনের মাধ্যমে ত্রিভুজটি নির্ধারণ করা যায়। এরূপ কয়েকটি সম্পাদ্য নিচে বর্ণনা করা হলো।
সম্পাদ্য ১.
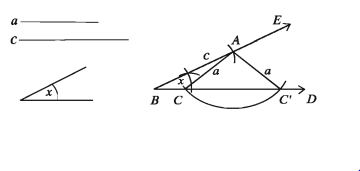
ত্রিভুজের ভূমি, ভূমি সংলগ্ন একটি কোণ ও অপর দুই বাহুর সমষ্টি দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।
মনে করি, কোনো ত্রিভুজের ভূমি a, ভূমি সংলগ্ন একটি কোণ Zx এবং অপর দুই বাহুর সমষ্টি s দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।
অঙ্কন:
১. যেকোনো একটি রশ্মি BE থেকে ভূমি a এর সমান করে BC রেখাংশ কেটে নিই। BC রেখাংশের B বিন্দুতে ∠x এর সমান ∠CBF আঁকি।
২. BF রশ্মি থেকে s এর সমান BD অংশ কাটি।
৩. C, D যোগ করি। C বিন্দুতে DC রেখাংশের যে পাশে B বিন্দু আছে সেই পাশে ∠BDC এর সমান ∠DCG আঁকি।
8. CG রশ্মি BD কে A বিন্দুতে ছেদ করে। তাহলে, ∆ABC ই উদ্দিষ্ট ত্রিভুজ।

প্রমাণ:
∆ACD এ ∠ADC = ∠ACD [অঙ্কন অনুসারে]
AC = AD
এখন, ∆ABC এ ∠ABC = ∠x, BC = a [অঙ্কন অনুসারে]
এবং BA + AC = BA + AD = BD = s
অতএব, ∆ABC ই নির্ণেয় ত্রিভুজ।
বিকল্প পদ্ধতি:
মনে করি, কোনো ত্রিভুজের ভূমি a, ভূমি সংলগ্ন একটি কোণ Zx এবং অপর দুই বাহুর সমষ্টি ৪ দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।
অঙ্কন:
১. যেকোনো একটি রশ্মি BE থেকে ভূমি a এর সমান করে BC রেখাংশ কেটে নিই। রেখাংশের B বিন্দুতে ∠x এর সমান ∠CBF আঁকি।
২. BF রশ্মি থেকে s এর সমান BD অংশ কাটি।
৩. C, D যোগ করি। CD এর লম্বদ্বিখণ্ডক PQ আঁকি।
8. PQ রশ্মি BD রশ্মিকে A এবং CD কে R বিন্দুতে ছেদ করে। A, C যোগ করি।
তাহলে, ∆ABC ই উদ্দিষ্ট ত্রিভুজ।

প্রমাণ:
∆ACR এবং ∆ADR এ CR = DR, AR = AR এবং অন্তর্ভুক্ত ∠ARC = অন্তর্ভুক্ত ∠ARD [সমকোণ ]
∆ACR = ∆ADR
AC = AD
এখন, ∆ABC এ ∠ABC = ∠x, BC = a [অঙ্কন অনুসারে]
এবং BA + AC = BA + AD = BD = s
অতএব, ∆ABC ই নির্ণেয় ত্রিভুজ।
সম্পাদ্য ২.
ত্রিভুজের ভূমি, ভূমি সংলগ্ন একটি সূক্ষ্মকোণ ও অপর দুই বাহুর অন্তর দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।
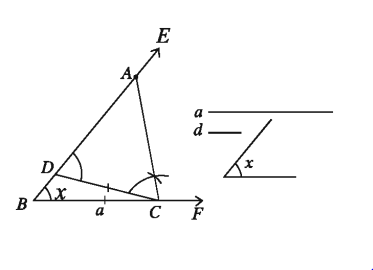
মনে করি, কোনো ত্রিভুজের ভূমি a, ভূমি সংলগ্ন সূক্ষ্মকোণ ∠x এবং অপর দুই বাহুর অন্তর d দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।
অঙ্কন:
১. যেকোনো একটি রশ্মি BF থেকে ভূমি a এর সমান করে BC রেখাংশ কেটে নিই। BC রেখাংশের B বিন্দুতে ∠x এর সমান ∠CBE আঁকি।
২. BE রশ্মি থেকে d এর সমান BD অংশ কেটে নিই।
৩. C, D যোগ করি। DC রেখাংশের যে পাশে E বিন্দু আছে সেই পাশে C বিন্দুতে ∠EDC এর সমান ∠DCA আঁকি। CA রশ্মি BE রশ্মিকে A বিন্দুতে ছেদ করে।
তাহলে, ∆ABC ই উদ্দিষ্ট ত্রিভুজ।
প্রমাণ:
অঙ্কন অনুসারে, ∆ACD এ ∠ACD = ∠ADC
AD = AC
সুতরাং দুই বাহুর অন্তর, AB – AC = AB – AD = BD = d
এখন, ∆ABC এ BC = a, AB – AC = d এবং ∠ABC = ∠a
সুতরাং, ∆ABC ই নির্ণেয় ত্রিভুজ।
সম্পাদ্য ৩.
ত্রিভুজের ভূমি সংলগ্ন দুইটি কোণ ও পরিসীমা দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।
মনে করি, একটি ত্রিভুজের পরিসীমা p এবং ভূমি সংলগ্ন দুইটি কোণ ∠x ও ∠y দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।
অঙ্কন:
১. যেকোনো একটি রশ্মি DF থেকে পরিসীমা এর সমান করে DE অংশ কেটে নিই। D ও E বিন্দুতে DE রেখাংশের একই পাশে ∠x এর সমান ∠EDL এবং ∠y এর সমান ∠DEM আঁকি।
২. কোণ দুইটির দ্বিখণ্ডক DG ও EH আঁকি ।
৩. মনে করি, DG ও EH রশ্মিদ্বয় পরস্পরকে A বিন্দুতে ছেদ করে। A বিন্দুতে ∠ADE এর সমান ∠DAB এবং ∠AED এর সমান ∠EAC আঁকি।
8. AB এবং AC রশ্মিদ্বয় DE রেখাংশকে যথাক্রমে B ও C বিন্দুতে ছেদ করে।
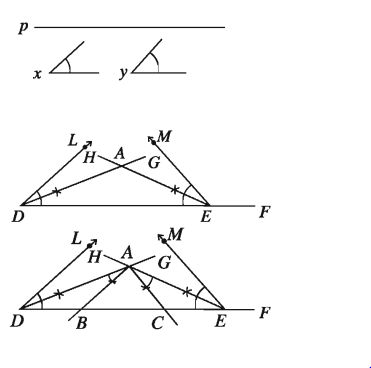
তাহলে, ∆ABC ই উদ্দিষ্ট ত্রিভুজ।
প্রমাণ:
∆ABD এ ∠ADB = ∠DAB [অঙ্কন অনুসারে]
AB = DB
আবার, ∆ACE এ ∠AEC = ∠EAC
CA = CE
সুতরাং ∆ABC এ AB + BC + CA = DB + BC + CE = DE = p
∠ABC = ∠ADB + ∠DAB = 1/2∠x + 1/2∠x = ∠x
এবং ∠ACB =∠AEC + ∠EAC = 1/2∠y+ 1/2∠y = ∠y
সুতরাং ∆ABC ই নির্ণেয় ত্রিভুজ।
উদাহরণ ১.
একটি ত্রিভুজ ABC আঁক, যার ∠B = 60°, ∠C = 45° এবং পরিসীমা AB + BC + CA = 11 সে.মি.।
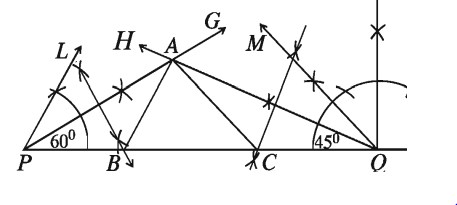
অঙ্কন:
নিচের ধাপসমূহ অনুসরণ করি:
১. রেখাংশ PQ = 11 সে.মি. আঁকি।
২. PQ রেখাংশের একই পাশে P এবং Q বিন্দুতে যথাক্রমে ∠QPL = 60° ও ∠PQM = 45° কোণ আঁকি ।
৩. কোণ দুইটির দ্বিখণ্ডক PG ও QH আঁকি। মনে করি, PG ও QH রশ্মিদ্বয় পরস্পরকে A বিন্দুতে ছেদ করে।
8. PA, QA রেখাংশের লম্ব সমদ্বিখণ্ডক আঁকি যা PQ রেখাংশকে যথাক্রমে B ও C বিন্দুতে ছেদ করে।
৫. A, B এবং A, C যোগ করি। তাহলে, ∆ABC ই উদ্দিষ্ট ত্রিভুজ।
উদাহরণ ২.
একটি ত্রিভুজের ভূমি a = 3 সে.মি., ভূমি সংলগ্ন সূক্ষ্মকোণ 45° এবং অপর বাহু দুইটির সমষ্টি 4 = 6 সে.মি.।
ক) উদ্দীপকের তথ্যগুলো চিত্রে প্রকাশ কর।
খ) ত্রিভুজ অঙ্কন কর। (অঙ্কনের চিহ্ন ও বিবরণ আবশ্যক)
গ) একটি বর্গের পরিসীমা 2s হলে বর্গটি আঁক। (অঙ্কনের চিহ্ন ও বিবরণ আবশ্যক)
সমাধান :
ক)
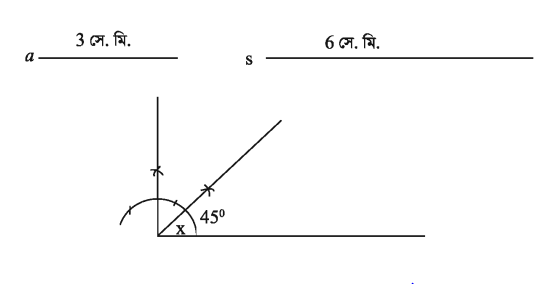
খ) AX যেকোনো রশ্মি থেকে AB = a কাটি । A বিন্দুতে ∠XAE = x আঁকি, AE থেকে = AD = s নেই। B, D যোগ করি। এবার B বিন্দুতে ∠ADB এর সমান করে ∠DBC আঁকি। BC রেখাংশ AD কে C বিন্দুতে ছেদ করে।
ABC উদ্দিষ্ট ত্রিভুজ।

গ) মনে করি, একটি বর্গের পরিসীমা P = 2s দেওয়া আছে, বর্গটি অঙ্কন করতে হবে।
AX যেকোনো রশ্মি থেকে AB = 1/4P কেটে নেই ।
A বিন্দুতে AE | AB আঁকি। AE থেকে AD = AB কাটি। এবার B ও D বিন্দুকে কেন্দ্র করে এর সমান 4P ব্যাসার্ধ নিয়ে ∠BAD এর অভ্যন্তরে দুইটি বৃত্তচাপ আঁকি। বৃত্তচাপদ্বয় পরস্পর C বিন্দুতে ছেদ করে। B, C এবং C, D যোগ করি।

∆BCD উদ্দিষ্ট বর্গক্ষেত্র।
