জ্যামিতি অনুশীলনী ২

আজকে আমরা  জ্যামিতি অনুশীলনী ২ সম্পর্কে  আলোচনা করবো । যা উচ্চতর গণিতের জ্যামিতি অংশের অন্তর্গত।

 

 

জ্যামিতি অনুশীলনী ২

১. নিচের বামের চিত্রে XY রেখাংশে AB এর লম্ব অভিক্ষেপ কোনটি?

ক) AB
খ) BC
গ) AC
ঘ) XY

 

 

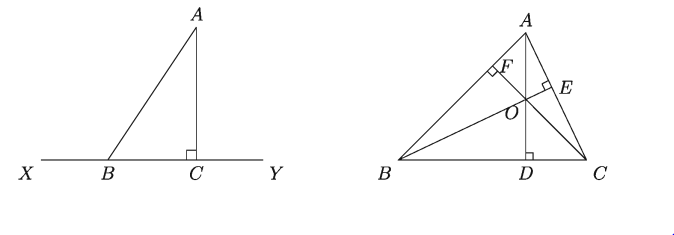
২. উপরের ডানের চিত্রে কোনটি লম্ববিন্দু?

ক) D
খ) E
গ) F
ঘ) 0

৩. একটি সমবাহু ত্রিভুজের প্রতিটি মধ্যমার দৈর্ঘ্য 3 সে.মি. হলে প্রতিটি বাহুর দৈর্ঘ্য কত?

ক) 4.5 সে.মি.
খ) 3.46 সে.মি.
গ) 4.24 সে.মি.
ঘ) 2.59 সে.মি.

 

 

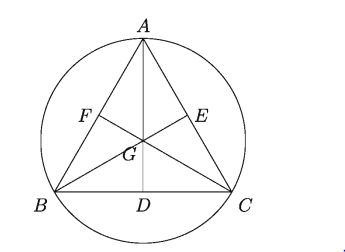
উপরের চিত্রে D, E, F যথাক্রমে BC, AC ও AB এর মধ্যবিন্দু। সেই আলোকে ৪-৬ নং প্রশ্নের উত্তর দাও:

8. G বিন্দুর নাম কী ?

ক) লম্ববিন্দু
খ) অন্তঃকেন্দ্র
গ) ভরকেন্দ্র
ঘ) পরিকেন্দ্র

৫. AABC এর শীর্ষ বিন্দু তিনটি দিয়ে অঙ্কিত বৃত্তের নাম কী?

ক) পরিবৃত্ত
খ) অন্তবৃত্ত
গ) বহির্বৃত্ত
ঘ) নববিন্দুবৃত্ত

৬. AABC এর ক্ষেত্রে নিচের কোনটি এ্যাপোলোনিয়াসের উপপাদ্যকে সমর্থন করে?

ক) AB2 + AC2 = BC2
গ)_AB2 + AC2 = 2 ( AC2 + GD2)
খ) AB2 + AC2 = 2 (AD2 + BD2)
ঘ) AB2 + AC2 = 2 (BD 2 + CD 2 )

৭. ABC ত্রিভুজের পরিবৃত্তস্থ যেকোনো বিন্দু P থেকে BC ও CA এর উপর PD ও PE লম্ব অঙ্কন করা হয়েছে। যদি ED রেখাংশ AB কে O বিন্দুতে ছেদ করে, তবে প্রমাণ কর যে, PO রেখা AB এর উপর লম্ব, অর্থাৎ PO | AB

৮. AABC এর LC সমকোণ। C থেকে অতিভুজের উপর অঙ্কিত লম্ব CD হলে, প্রমাণ কর যে, CD2 = AD. BD

৯. AABC এর শীর্ষত্রয় থেকে বিপরীত বাহুগুলোর উপর লম্ব AD, BE ও CF রেখাত্রয় O বিন্দুতে ছেদ করে। প্রমাণ কর যে, AO OD = BO – OE = CO. OF 1 [সংকেত: ABOF এবং ACOE সদৃশ। . BO : CO = OF : OE 1]

১০. AB ব্যাসের উপর অঙ্কিত অর্ধবৃত্তের দুইটি জ্যা AC ও BD পরস্পর P বিন্দুতে ছেদ করে। প্রমাণ কর যে, AB2 = AC . AP + BD. BP

১১. কোনো সমবাহু ত্রিভুজের পরিবৃত্তের ব্যাসার্ধ 3 সে.মি. হলে ঐ ত্রিভুজের বাহুর দৈর্ঘ্য নির্ণয় কর।

১২. ABC সমদ্বিবাহু ত্রিভুজের শীর্ষবিন্দু A হতে ভূমি BC এর উপর অঙ্কিত লম্ব AD এবং ত্রিভুজের পরিব্যাসার্ধ R হলে প্রমাণ কর যে, AB2 = 2R · AD।

১৩. ABC ত্রিভুজের ZA এর সমদ্বিখণ্ডক BC কে D বিন্দুতে এবং ABC পরিবৃত্তকে E বিন্দুতে ছেদ করেছে। দেখাও যে, AD2 = AB – AC BD.DC1

১৪. ABC ত্রিভুজের AC ও AB বাহুর উপর যথাক্রমে BE ও CF লম্ব। দেখাও যে, AABC:AAEF = AB2 : AE

১৫. APQR এ PM, QN ও RS মধ্যমাত্রয় O বিন্দুতে ছেদ করেছে।

 

 

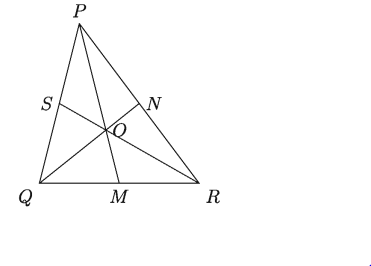
ক) O বিন্দুটির নাম কী? O বিন্দু PM কে কী অনুপাতে বিভক্ত করে?
খ) APQR হতে PQ2 + PR2 = 2 (PM2 + QM 2 ) সম্পর্কটি প্রতিষ্ঠিত কর।
গ) দেখাও যে, APQR এর বাহু তিনটির বর্গের সমষ্টি O বিন্দু হতে শীর্ষবিন্দু তিনটির দূরত্বের বর্গের সমষ্টির তিনগুণ।

১৬. নিচের চিত্রে S, O যথাক্রমে AABC এর পরিকেন্দ্র ও লম্ববিন্দু। AP মধ্যমা, BC AC = b এবং AB = cl = a,

 

 

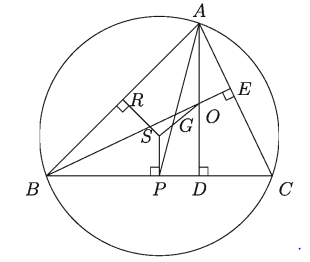
ক) OA এবং SP এর মধ্যে সম্পর্ক নির্ণয় কর।
খ) দেখাও যে, S, G, O একই সরল রেখায় অবস্থিত।
গ) LC সূক্ষ্মকোণ হলে a · CD = b. CE সমীকরণটি প্রতিষ্ঠিত কর।