আজকে আমাদের আলোচনার বিষয়ঃ তথ্য ও উপাত্ত লেখচিত্র । এটি অষ্টম শ্রেনী গণিতের তথ্য ও উপাত্ত এর অন্তর্গত।
তথ্য ও উপাত্ত লেখচিত্র
তথ্য ও উপাত্ত লেখচিত্রের মাধ্যমে উপস্থাপন একটি বহুলপ্রচলিত পদ্ধতি। কোনো পরিসংখ্যানে ব্যবহৃত উপাত্ত লেখচিত্রের মাধ্যমে উপস্থাপিত হলে তা বোঝা ও সিদ্ধান্ত গ্রহণের জন্য খুব সুবিধাজনক হয় । অধিকন্তু চিত্রের মাধ্যমে উপস্থাপিত উপাত্ত চিত্তাকর্ষকও হয়। তাই বুঝা ও সিদ্ধান্ত গ্রহণের সুবিধার্থে উপাত্তসমূহের গণসংখ্যা নিবেশনের চিত্র লেখচিত্রের মাধ্যমে উপস্থাপন করা হয়। গণসংখ্যা নিবেশন উপস্থাপনে বিভিন্ন রকম লেখচিত্রের ব্যবহার থাকলেও এখানে কেবলমাত্র আয়তলেখ ও পাইচিত্র নিয়ে আলোচনা করা হবে ।
আয়তলেখ (Histogram) :
গণসংখ্যা নিবেশনের একটি লেখচিত্র হচ্ছে আয়তলেখ । আয়তলেখ অঙ্কনের জন্য ছক কাগজে x ও y-অক্ষ আঁকা হয় । x-অক্ষ বরাবর শ্রেণিব্যাপ্তি এবং y-অক্ষ বরাবর গণসংখ্যা নিয়ে আয়তলেখ আঁকা হয় । আয়তের ভূমি হয় শ্রেণিব্যাপ্তি এবং উচ্চতা হয় গণসংখ্যা ।
উদাহরণ ১।
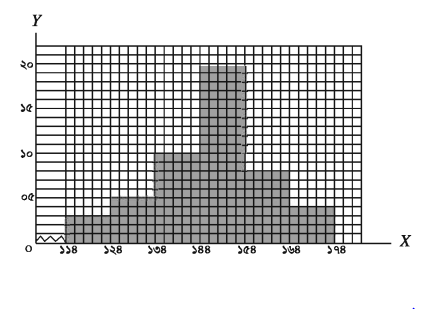
নিচে ৫০ জন শিক্ষার্থীর উচ্চতার গণসংখ্যা নিবেশন দেওয়া হলো । একটি আয়তলেখ আঁক।
|
উচ্চতার শ্রেণিব্যাপ্তি (সেমিতে) |
১১৪-১২৪ |
১২৪-১৩৪ |
১৩৪-১৪৪ |
১৪৪-১৫৪ |
১৫৪–১৬৪ |
১৬৪–১৭৪ |
|
গণসংখ্যা (শিক্ষার্থীর সংখ্যা) |
৩ |
৫ |
১০ |
২০ |
৮ |
৪ |
ছক কাগজের ১ ঘর সমান শ্রেণিব্যাপ্তির ২ একক ধরে x – অক্ষে শ্রেণিব্যাপ্তি এবং ছক কাগজের ১ ঘর সমান গণসংখ্যার ১ একক ধরে y-অক্ষে গণসংখ্যা নিবেশন স্থাপন করে গণসংখ্যা নিবেশনের আয়তলেখ আঁকা হলো। x-অক্ষের মূলবিন্দু থেকে ১১৪ ঘর পর্যন্ত ভাঙা চিহ্ন দিয়ে আগের ঘরগুলো বিদ্যমান বোঝানো হয়েছে ।
পাইচিত্র (Pie Chart):
পাইচিত্রও একটি লেখচিত্র । অনেক সময় সংগৃহীত পরিসংখ্যান কয়েকটি উপাদানের সমষ্টি দ্বারা গঠিত হয় অথবা একে কয়েকটি শ্রেণিতে ভাগ করা হয়। এ সকল ভাগকে একটি বৃত্তের অভ্যন্তরে বিভিন্ন অংশে প্রকাশ করলে যে লেখচিত্র পাওয়া যায় তাই পাইচিত্র । পাইচিত্রকে বৃত্তলেখও বলা হয়। আমরা জানি, বৃত্তের কেন্দ্রে সৃষ্ট কোণের পরিমাণ ৩৬০° । কোনো পরিসংখ্যান ৩৬০° এর অংশ হিসেবে উপস্থাপিত হলে তা হবে পাইচিত্র।
আমরা জানি, ক্রিকেটখেলায় ১, ২, ৩, ৪, ও ৬ করে রান সংগৃহীত হয়। তাছাড়া নো-বল ও ওয়াইড বলের জন্য অতিরিক্ত রান সংগৃহীত হয়। কোনো-এক খেলায় বাংলাদেশ ক্রিকেট দলের সংগৃহীত রান নিচের সারণিতে দেওয়া হলো :
| রান সংগ্রহ |
১ করে |
২ করে |
৩ করে |
৪ করে |
৬ করে |
অতিরিক্ত রান |
মোট |
| বিভিন্ন প্রকারের সংগৃহীত রান |
৬৬ |
৫০ |
৩৬ |
৪৮ |
৩০ |
১০ |
২৪০ |
ক্রিকেটখেলার উপাত্ত পাইচিত্রের মাধ্যমে দেখানো হলে, বোঝার জন্য যেমন সহজ হয় তেমনি চিত্তাকর্ষকও হয় । আমরা জানি, বৃত্তের কেন্দ্রে সৃষ্ট কোণ ৩৬০°। উপরে বর্ণিত উপাত্ত ৩৬০°-এর অংশ হিসেবে উপস্থাপন করা হলে, উপাত্তের পাইচিত্র পাওয়া যাবে ।
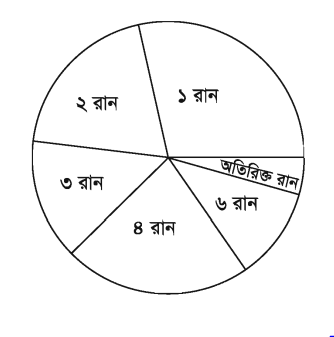
২৪০ রানের জন্য কোণ = ৩৬০°
১ রানের জন্য কোণ = ৩৬০°/২৪০
৬৬ রানের জন্য কোণ = (৬৬ × ৩৬০°)/২৪০ = ১৯০
৫০ রানের জন্য কোণ = (৫০ × ৩৬০°)/২৪০ = ৭৫°
৩৬ রানের জন্য কোণ = (৩৬ × ৩৬০°)/২৪০ = ৫৪°
৪৮ রানের জন্য কোণ = (৪৮ × ৩৬০°)/২৪০ = ৭২°
১০ রানের জন্য কোণ = (১০ × ৩৬০°)/২৪০ = ১৫°
এখন, প্রাপ্ত কোণগুলো ৩৬০°-এর অংশ হিসাবে আঁকা হলো। যা বর্ণিত উপাত্তের পাইচিত্র।
উদাহরণ ২।
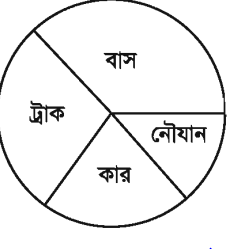
কোনো এক বছরে দুর্ঘটনাজনিত কারণে সংঘটিত মৃত্যুর সারণি নিচে দেয়া হলো । একটি পাইচিত্র আঁক ।
|
দুর্ঘটনা |
বাস |
ট্রাক |
কার |
নৌযান |
মোট |
|
মৃতের সংখ্যা |
৪৫০ |
৩৫০ |
২৫০ |
১৫০ |
১২০০ |
সমাধান :
বাস দুর্ঘটনায় মৃত ৪৫০ জনের জন্য কোণ = (৪৫০/১২০০)× ৩৬০° = ১৩৫°
ট্রাক দুর্ঘটনায় মৃত ৩৫০ জনের জন্য কোণ = (৩৫০/১২০০) × ৩৬০° = ১০৫°
কার দুর্ঘটনায় মৃত ২৫০ জনের জন্য কোণ = (২৫০/১২০০) × ৩৬০° = ৭৫°
নৌযান দুর্ঘটনায় মৃত ১৫০ জনের জন্য কোণ = (১৫০/১২০০) × ৩৬০° = 84°
এখন, কোণগুলো ৩৬০° এর অংশ হিসাবে আঁকা হলো, যা নির্ণেয় পাইচিত্র ।
উদাহরণ ৩।
দুর্ঘটনায় মৃত ৪৫০ জনের মধ্যে কতজন নারী, পুরুষ ও শিশু তা পাইচিত্রে দেখানো হয়েছে । নারীর জন্য নির্দেশিত কোণ ৮০°। নারীর সংখ্যা কত ?
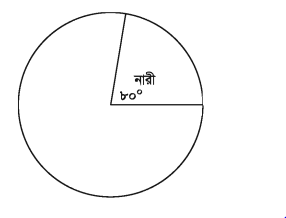
সমাধান :
আমরা জানি, বৃত্তের কেন্দ্রে সৃষ্ট কোণ ৩৬০° ।
সুতরাং ৩৬০° এর জন্য ৪৫০ জন
১° এর জন্য জন্য ৪৫০/৩৬০ জন
৮০° এর জন্য ৪৫০/৩৬০ x ৮০ জন = ১০০ জন
নির্ণেয় নারীর সংখ্যা ১০০ জন ।
