আজকে আমরা আলোচনা করবো ত্রিকোণমিতিক অনুপাতসমূহ । যা উচ্চতর গণিতের ত্রিকোণমিতি অংশের অন্তর্গত।

ত্রিকোণমিতিক অনুপাতসমূহ
ত্রিকোণমিতির এই অংশে প্রথমে সূক্ষ্মকোণের ক্ষেত্রে ত্রিকোণমিতিক অনুপাতসমূহ (sine, cosine, tangent, secant, cosecant, cotangent) সম্পর্কে আলোচনা করা হবে। সূক্ষ্মকোণের অনুপাতসমূহের মাধ্যমে যেকোনো কোণের ত্রিকোণমিতিক অনুপাতসমূহ নির্ণয়ের কৌশল আলোচনা করা হবে। অনুপাতসমূহের পারস্পরিক সম্পর্ক এবং বিভিন্ন চতুর্ভাগে এদের চিহ্ন কি হবে সে সম্পর্কে ব্যাখ্যা করা হবে। ত্রিকোণমিতিক অনুপাত সংক্রান্ত কতিপয় অভেদ সম্পর্কে ধারণা দেওয়া হবে ।
এছাড়াও আদর্শ কোণসমূহের (o, π/6, π/4,π/3, π/2) ত্রিকোণমিতিক অনুপাত এবং অনুপাতসমূহের সর্বোচ্চ বা সর্বনিম্নমান অর্থাৎ মানের পরিধি সম্পর্কে আলোচনাও এই অংশে অন্তর্ভুক্ত থাকবে।
(ক) সূক্ষ্মকোণের ত্রিকোণমিতিক অনুপাতসমূহ (Trigonometric Ratios of Acute Angles):
সূক্ষ্মকোণের ত্রিকোণমিতিক অনুপাতসমূহ নির্ণয় করার জন্য আমরা একটি সমকোণী ত্রিভুজ AOPQ বিবেচনা করি। AOPQ এ LOQP সমকোণ। ZPOQ এর সাপেক্ষে OP ত্রিভুজের অতিভুজ (hypotenuse), OQ ভূমি (adjacent side), PQ লম্ব (opposite side) এবং ZPOQ = 6 (সূক্ষ্মকোণ)। OPQ সমকোণী ত্রিভুজে সূক্ষ্মকোণ ৪ এর জন্য ছয়টি ত্রিকোণমিতিক অনুপাত (sine, cosine, tangent, secant, cosecant, cotangent) নিম্নোক্তভাবে সংজ্ঞায়িত করা হয়:
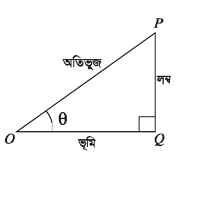
sin8 = PQ/OP = লম্ব /অতিভুজ
cosec8 = OP/PQ = অতিভুজ/ লম্ব
cos8 = OQ/OP = ভূমি /অতিভুজ
sec8 = OP/OQ = অতিভুজ/ভূমি
tan8 = PQ/OQ = লম্ব/ভূমি
cot8 =OQ/PQ= ভূমি/লম্ব
উদাহরণ ১০.
একটি সমকোণী ত্রিভুজের ক্ষেত্রে tane 3 হলে অন্য ত্রিকোণমিতিক অনুপাতসমূহ = নির্ণয় কর।
সমাধান:
ধরি, ABC একটি সমকোণী ত্রিভুজ যেখানে অতিভুজ = AC, ভূমি = AB, লম্ব = BC এবং ∠BAC = 8
দেওয়া আছে tan8 = লম্ব/ভূমি = 3/1
লম্ব BC = 3 একক এবং ভূমি AB = 1 একক।
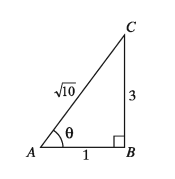
পিথাগোরাসের উপপাদ্য অনুযায়ী
অতিভুজ AC =√(AB2 + BC2 )= √(12 + 32) = √10 একক
অন্য ত্রিকোণমিতিক অনুপাতসমূহ
sine8 = লম্ব/অতিভুজ = 3/√10
cosec8 = অতিভুজ /লম্ব =√10/ 3
cos8 =ভূমি /অতিভুজ = 1/√10
sec8 = অতিভুজ/ভূমি = √10/1 = √10
এবং cot8 = ভূমি/লম্ব = 1/ 3
লক্ষণীয় :
যেহেতু অনুপাতের কোনো একক থাকেনা এবং sine, cosine, tangent, secant, cosecant, cotangent এই ছয়টি ত্রিকোণমিতিক অনুপাত, তাই এদের কোনো একক নাই।
দ্রষ্টব্য:
ত্রিকোণমিতিক অনুপাতসমূহকে সংক্ষেপে লিখা হয়। যেমন:
sine8 = sin8, cosine8 = cos8, tangent8 = tan8,
secant8 = sec8, cosecant8 = cosec8, cotangent8 = cot8
(খ) যেকোনো কোণের জন্য ত্রিকোণমিতিক অনুপাতসমূহ:
এই অংশে আমরা যেকোনো কোণের জন্য ত্রিকোণমিতিক অনুপাতসমূহ নির্ণয় করব। সে জন্য আমাদের কোণটির প্রমিত বা আদর্শ অবস্থান (Standard position) জানা দরকার। কার্তেসীয় সমতলে মূলবিন্দু থেকে ডানদিকে অর্থাৎ ধনাত্মক x-অক্ষকে আদি রশ্মি ধরে কোণটি অঙ্কন করলেই এর আদর্শ অবস্থান পাওয়া যায়। এখানে 6 কে আমরা ত্রিকোণমিতিক কোণ হিসাবে বিবেচনা করব অর্থাৎ ৪ কোণের পরিমাণ নির্দিষ্ট সীমার মধ্যে থাকবে না ।
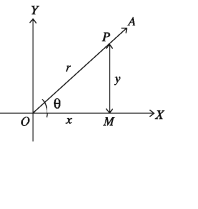
মনে করি, কার্তেসীয় তলে XOX রেখা -অক্ষ, Y’OY রেখা y-অক্ষ এবং O বিন্দু মূলবিন্দু । ঘূর্ণায়মান রশ্মি OA ধনাত্মক x-অক্ষ অর্থাৎ OX রশ্মি থেকে শুরু করে ঘড়ির কাঁটার বিপরীত দিকে (anticlockwise) ঘুরে OA অবস্থানে ৪ কোণ উৎপন্ন করেছে (নিচের চিত্র)।
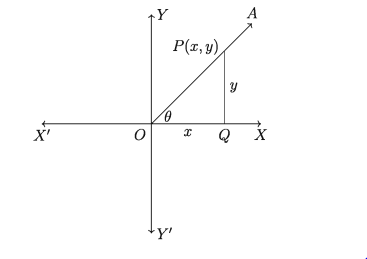
OX কে ৪ কোণের আদিবাহু (initial side) এবং OA কে প্রান্তিকবাহু (terminal side) বলা হয়। OA প্রান্তিক বাহুর উপর O বিন্দু ভিন্ন P(x, y) একটি বিন্দু নিই। তাহলে OX থেকে বিন্দুটির লম্ব দূরত্ব Y, OY থেকে এর লম্ব দূরত্ব এবং ZOQP সমকোণ (উপরের চিত্র)।
সুতরাং পীথাগোরাসের সূত্র অনুসারে অতিভুজ |OP| = r = Vz2 + y2 । তাহলে যে কোনো কোণ ও এর জন্য ত্রিকোণমিতিক অনুপাতসমূহ হবে:
sin8 = লম্ব /অতিভুজ = y/r
cos8 = ভূমি /অতিভুজ = x/r
tan8 = লম্ব/ভূমি = y/x [x ≠ 0]
sec8 = অতিভুজ/ভূমি = r/x [x ≠ 0]
cosec8 = অতিভুজ/ লম্ব = r/y [y ≠ 0]
cot8 = ভূমি/লম্ব = x/y [y ≠ 0]
লক্ষণীয় ১:
P এবং O বিন্দু ভিন্ন হওয়ায় |OP | > 0 এবং sine ও cos সবসময়ই অর্থবহ। OA প্রান্তিক বাহু -অক্ষের উপর থাকলে y = 0 হয় বলে এরূপ কোণের জন্য cosecfi ও cot সংজ্ঞায়িত নয়।
অনুরূপভাবে, OA প্রান্তিক বাহু y-অক্ষের উপর থাকলে x = 0 হয় এবং এরূপ কোণের জন্য sec8 ও tan8 সংজ্ঞায়িত হয় না।
লক্ষণীয় ২:
প্রান্তিক বাহু OA এর উপর P(x, y) বিন্দু ভিন্ন অন্য কোনো বিন্দু P1 (x1, y1 ) নিই (নিচের বামের চিত্র ও ডানের চিত্র)। P(x, y) 3 P1 (x1, y1 ) বিন্দুদ্বয় থেকে :- অক্ষের উপর PM ও P1M1 লম্ব আঁকি। তাহলে ∆OPM এবং ∆OP1M1 সদৃশ।
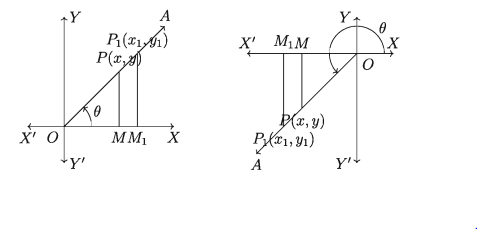
অর্থাৎ | x|/ |x₁|= | y|/ |y₁| = | OP | |OP₁| = r/ r₁
এখানে, OP = r, OP1 = r1 x ও x₁ এবং y ও Y1 একই চিহ্নযুক্ত।
x/ x₁= y/ y₁ = r/ r₁ অর্থাৎ, x/r = x₁/ r₁ এবং y/r = y₁/ r₁
সুতরাং sin8 = y/r = y₁/ r₁
cos8 = x/r = x₁/ r₁
tan8 = x/ x₁= y/ y₁ ইত্যাদি।
সিদ্ধান্ত:
ত্রিকোণমিতিক অনুপাতসমূহের মান প্রান্তিক রশ্মি OA এর উপর নির্বাচিত বিন্দু P এর উপর নির্ভর করে না।
লক্ষণীয় ৩:
৪ সূক্ষ্মকোণ হলে প্রমিত বা আদর্শ অবস্থানে এর প্রান্তিক বাহু OA প্রথম চতুর্ভাগে থাকে এবং 0 = ZXOA হয় (পাশের চিত্র)। OA বাহুতে যেকোন বিন্দু P(2, 3) নিয়ে এবং P থেকে OX এর উপর PM লম্ব টেনে দেখা যায় যে, OM = 2, PM = y এবং OP = ধরে পূর্ববর্তী আলোচনার (ক) ও (খ) থেকে ৪ কোণের অনুপাতগুলোর একই মান পাওয়া যায়।
(গ) ত্রিকোণমিতিক অনুপাতগুলোর পারস্পরিক সম্পর্ক :
ত্রিকোণমিতিক অনুপাতসমূহের সংজ্ঞা থেকে আমরা লক্ষ করি যে, লম্ব অতিভুজ’ sino coseco অতিভুজ 1 লম্ব লম্ব অতিভুজ 1
sine8 = লম্ব/অতিভুজ, cosec8 = অতিভুজ /লম্ব = 1/ (লম্ব/অতিভুজ) = 1/ sine8
sine8 = 1/ cosec8 , cosec8 = 1/ sine8
অনুরূপভাবে,
cos8 =ভূমি /অতিভুজ , sec8 = অতিভুজ/ভূমি = 1 /(অতিভুজ/ভূমি) = 1/cos8
cos8 =1/ sec8 , sec8 = = 1/cos8
tan8 = 1/cot8 , cot8 =1/tan8
ত্রিকোণমিতিক অনুপাত সংক্রান্ত কতিপয় সহজ অভেদাবলী (Identities):
(i) sin 20 + cos 20 = 1
প্রমাণ:
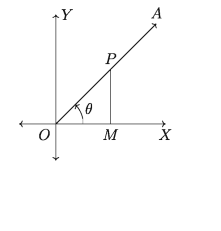
পাশের চিত্র থেকে আমরা দেখি, cose ভূমি /অতিভুজ = x/r
sine = লম্ব / অতিভুজ = y/r
এবং r2 = x2 + y2
sin²0 + cos²0 = x2 /r2 + y2/r2 = x2 + y2/r2 = r2/r2 = 1
sin20+ cos20 1 = 1 (প্রমাণিত)।
(i) নং সূত্র থেকে আমরা পাই, sin20 = 1 – cos 20
বা, cos 20 = 1 – sin 20
অনুরূপভাবে প্রমাণ করা যায় যে,
(ii) 1 + tan 20 = sec20 বা, sec20 – 1 = tan20
(iii) 1+cot20 = cosec20, cosec20-1 = cot20
বিভিন্ন চতুর্ভাগে ত্রিকোণমিতিক অনুপাতসমূহের চিহ্ন
পাশের চিত্রে কার্তেসীয় তলকে XOX এবং Y’OY অক্ষদ্বয় দ্বারা চারটি চতুর্ভাগ (Quadrant) যথাক্রমে XOY (১ম চতুৰ্ভাগ), YOX’ (২য় চতুৰ্ভাগ), X’OY’ (৩য় চতুৰ্ভাগ) এবং Y’OX (৪র্থ চতুৰ্ভাগ) বিভক্ত করা হয়েছে।
আদি অবস্থান OX থেকে একটি রশ্মি OA, ঘড়ির কাঁটার বিপরীত দিকে ঘূর্ণনের ফলে OA এর প্রান্তিক অবস্থানের উপর নির্ভর করে বিভিন্ন কোণ উৎপন্ন হবে। ঘূর্ণায়মান রশ্মি OA এর উপর যেকোনো বিন্দু P(x, y) নিই। তাহলে |OP| = r. প্রান্তিক রশ্মি OA এবং P বিন্দুর বিভিন্ন চতুর্ভাগে অবস্থানের সঙ্গে সঙ্গে x ও y এর চিহ্ন পরিবর্তন হবে কিন্তু ” সবসময় ধনাত্মক থাকবে।
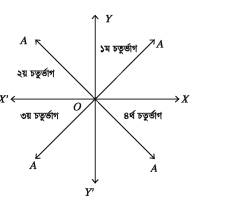
OA রশ্মি যখন প্রথম চতুর্ভাগে থাকে, তখন ও y এর মান ধনাত্মক। তাই প্রথম চতুর্ভাগে সকল ত্রিকোণমিতিক অনুপাত ধনাত্মক। OA রশ্মি যখন দ্বিতীয় চতুর্ভাগে থাকে তখন P বিন্দুর ভুজ : ঋণাত্মক এবং কোটি y ধনাত্মক। এজন্য দ্বিতীয় চতুর্ভাগে sin (sin8 = =y/r) এবং cosec (cosec8 = r/y) অনুপাত দুইটি ধনাত্মক। অন্যসব অনুপাত ঋণাত্মক।
একইভাবে তৃতীয় চতুর্ভাগে P বিন্দুর ভুজ ও কোটি y উভয়ই ঋণাত্মক এবং tan (tane = -y/-x =y/x) ও cot (cote = -x/-y = x/y) ধনাত্মক। অন্য অনুপাতসমূহ ঋণাত্মক।
চতুর্থ চতুর্ভাগে OA রশ্মির উপর P বিন্দুর ভুজ : ধনাত্মক এবং কোটি y ঋণাত্মক বলে cos (cose = x/r) এবং sec (sece = r/x) ধনাত্মক এবং অন্যসব ত্রিকোণমিতিক = অনুপাত ঋণাত্মক।
আবার, x অক্ষের যেকোনো অবস্থানে y এর মান শূন্য বলে cosec (cosec8 = r/y) এবংcot (cot8 = x/y) অনুপাত দুইটি সংজ্ঞায়িত নয়।
অনুরূপভাবে, y-অক্ষের যেকোনো অবস্থানে x এর মান শূন্য। তাই y-অক্ষের উপর sec (sece = r/x) এবং tan (tane = y/x) সংজ্ঞায়িত নয়। sin (sin8 =y/r) এবং cos (cose = x/r) অনুপাত দুইটি P বিন্দুর যেকোনো অবস্থানেই সংজ্ঞায়িত এবং বাস্তব মান আছে।
উপরোক্ত আলোচনার সারাংশ নিম্নের চিত্রে দেখানো হলো। উক্ত চিত্রের সাহায্যে যেকোনো কোণের প্রান্তিক রশ্মির অবস্থানের উপর নির্ভর করে উক্ত কোণের সকল ত্রিকোণমিতিক অনুপাতের চিহ্ন নির্ণয় সহজ হবে।

ত্রিকোণমিতিক অনুপাতসমূহ
নবম-দশম শ্রেণির গণিতে সূক্ষ্মকোণের ত্রিকোণমিতিক অনুপাত সম্পর্কে আলোচনা করা হয়েছে। আমরা এখানে যেকোনো কোণের ত্রিকোণমিতিক অনুপাত সমূহ বর্ণনা করবো।
কোণের প্রমিত অবস্থান (Standard Position) কার্তেসীয় তলে মূল বিন্দু O তে ধনাত্মক :-অক্ষকে আদি রশ্মি ধরে কোণ অঙ্কন করলে কোণটির প্রমিত অবস্থান পাওয়া যায়।
অনুপাতসমূহের সংজ্ঞা
8 যেকোনো কোণ। এর প্রমিত অবস্থানে ঘূর্ণায়মান রশ্মি OZ এর উপর বিন্দু P(x, y) নিই যেখানে OP = r( > 0)। তাহলে ৪ কোণের
sine অনুপাত sin8 =y/r
cosine অনুপাত, cos8 = x/r
tangent অনুপাত, tan8 = y/x [যখন x ≠ 0]
cotangent অনুপাত, cot8 = x/y [ যখন y ≠ 0 ]
secant অনুপাত্ত, sec8= r/x [যখন x ≠ 0]
cosecant অনুপাত, cosec8 [যখন y ≠ 0]
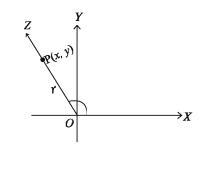
লক্ষণীয় যে, রশ্মি OZ এর ওপর P(zy), P(z, s/) দুইটি PROP=r(> 0), OP’ = r'(> 0); x, 2º এবং y, / একই চিহ্নযুক্ত। ফলে ∠OPM ও ∠OPM হতে পাই।
x/r = x₁/ r₁,y/r = y₁/ r₁ ইত্যাদি।
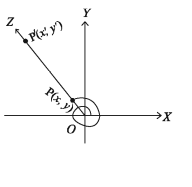
ফলে ও কোণের অনুপাত সমূহের মান OZ রশ্মিতে P বিন্দুর অবস্থানের উপর নির্ভর করে না।
৪ সূক্ষ্মকোণ হলে ∠OPM সমকোণী ত্রিভুজে অভিভুজ OP = r, সন্নিহিত বাহু OM = x, বিপরীত বাহু PM = y সুতরাং,
sin৪ = y/r = বিপরীত বাহু/ অতিভুজ
cos৪ = x/r = সন্নিহিত বাহু/ অতিভুজ
tan৪ = x/y = বিপরীত বাহু/ সন্নিহিত বাহু
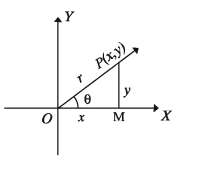
সুতরাং সুক্ষ্মকোণের ক্ষেত্রে ত্রিকোণমিতিক অনুপাতের স্থানাঙ্ক ভিত্তিক সংজ্ঞা ও নবম-দশম শ্রেণি গণিত বইয়ের প্রদত্ত সমকোণী ত্রিভুজভিত্তিক সংজ্ঞা একই।
0° এবং 90° কোণের অনুপাত সমূহ: কোণের ক্ষেত্রে ঘূর্ণায়মান রশ্মি OX রেখার ওপর থাকে। সুতরাং P(20) এবং r = OP = 2.
অতএব,
sin0 = y/r = 0/r = 0
cos0 = x/r = = x/x = 1
90° কোণের ক্ষেত্রে ঘূর্ণায়মান রশ্মি OY রেখার ওপর থাকে। সুতরাং P(0,y) এবং r = OP = y
sin90°= y/r = y/y = 1
cos90° = x/r = = 0/r = 0
সংজ্ঞা থেকে সহজেই দেখা যায়, যেকোনো কোণের জন্য ত্রিকোণমিতিক অনুপাতের নির্মোপ্ত ধর্মাবলী প্রযোজ্য।
3. sin28+ cos28=1

প্রমাণ:
sin8 = y/r
cos8 = x/r
sin28+ cos28 = x2 + y2/r2 = r2/r2 = 1
2. tan8= sin8 /Cos8 ,cot8= sin8/cos8
sec8 = 1/cos8, cosec8 =1/sin8
যেখানে অনুপাতগুলো সংজ্ঞায়িত।
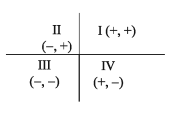
৩. উপরের চিত্রে প্রদত্ত স্থানাঙ্ক চিহ্ন বিবেচনা করে দেখা যায় য
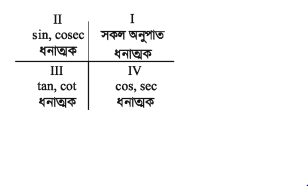
8. |sin8| ≤ 1, |cos8| ≤ 1
প্রমাণ:
sin²8+ cos²8 = 1
sin²8 ≤ 1, cos²8 ≤1
sine≤ 1, cose ≤1
৫. ও এর বিভিন্ন মানের জন্য sine, cos এবং tan এর মান নিম্নরূপ:
|
0° |
π/6 = 30° |
π/4 = 45° |
π/3 = 60° |
π/2 = 90° |
|
| sin8 |
0 |
1/2 |
1/√2 |
√3/2 |
1 |
| cos8 |
1 |
√3/2 |
1/√2 |
1/2 |
0 |
| tan8 |
0 |
1/√3 |
1 |
√3 |
অসঙ্গায়িত |
উদাহরণ ১১.
8 সূক্ষ্মকোণ (0 <8 <π/2) এবং cos8 = 4 /5 হলে, অপর ত্রিকোণমিতিক অনুপাতসমূহের মান নির্ণয় কর।
সমাধান:
ত্রিকোণমিতিক অভেদ (Identities) ব্যবহার করে।
আমরা জানি,
sin²8 + cos²8 = 1
sin² = 1 – cos²0
= 1- (4/5)2
= 1- (16 /25)
= (25-16)/25
= 9/ 25
sin8 = √(9 /25)
= 3/5
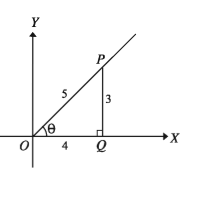
এখন ∆POQ সমকোণী ত্রিভুজ থেকে পাই,
tan8= লম্ব/ ভূমি = (লম্ব/অতিভুজ )/(ভূমি/অতিভুজ) = (PQ / OP )/ (OQ/OP)
sin8/ cos 8 = (3/5 )/(4/5) = 3/4
cot8= ভূমি/লম্ব= (ভূমি/অতিভুজ)/(লম্ব/অতিভুজ ) = (OQ/OP)/(PQ / OP )
cos8/ sin8 = (4/5 )/(3/5) = 4/3
tan8 = sin8/ cos 8
cote = cos 8/ sin8
ত্রিকোণমিতিক অভেদের সাহায্যে,
tan20 = sec20 – 1
= (5/3)2 -1= 25/9 -1= -1= 16/9
cot8= √(16/ 9) = 4/ 3
বিকম্প:
আমরা জানি,
cost8= ভূমি/ অতিভুজ
= 4/5 [দেওয়া আছে]
পাশের চিত্রে সমকোণী ত্রিভুজ POQ থেকে পাই,
PQ = √(OP2 OQ2) = √(52-42) =√(25-16) = √9 = 3 একক
sin8 = লম্ব/ অতিভুজ
=PQ/ OP
= 3/5
tan8 = লম্ব /ভূমি
= PQ/OQ
= 3/4
sece= অতিভুজ/ ভূমি
= OP/ PQ
= 5 /4
coseco = অতিভুজ /লম্ব
=OP/ PQ
= 5/3
cote = ভূমি/ লম্ব
= OQ/ PQ
= 4/3

উদাহরণ ১২.
cosA= 3/5 , sinB = 12/13 এবং A ও B উভয়ই সূক্ষ্মকোণ হলে (tanA – tanB)/ ( 1 + tanB. tanA)এর মান নির্ণয় কর।
সমাধান:
দেওয়া আছে, cosA= 4/5
আমরা জানি, sin2 A + cos2 A = 1
বা, sin2 A = 1 – cos2A
বা, 1- (16 /25)
= 9/25
বা, sinA = √(9/25 )
= 3/5 [A সূক্ষ্মকোণ]
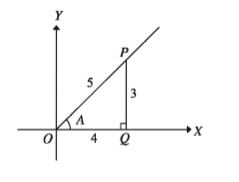
tanA= sinA /cos A
=(3/5)/ (4/5)
=3/4
আবার , sinB = 12 /13
cosB= √(1-sin2B)
=√ (1- 144/ 169)
= 25/169
cosB=5/13
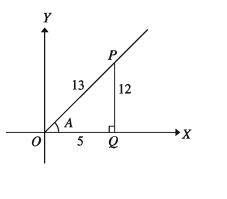
tanB= sin B /cos B = (12/13)/( 5/13) =12/5
এখন, (tanA – tanB)/ ( 1 + tanB. tanA)
= {(12/5)-(3/4)}/{1+(12/5).(3/4)}
= {(48-15)/20}/{1+{36/20)}
= (33/20)/{(20+36)/20}
= 33/56
(tanA – tanB)/ ( 1 + tanB. tanA) =33/56
উদাহরণ ১৩
মান নির্ণয় কর : sin²π/6+cos²π/4+tan2π/3+cot2π/2
সমাধান:
আমরা জানি, sinπ/6 = 1/2 , COSπ/4 = 1 /√2, tanπ/3 = √3 এবং cotπ/2 = 0
sin²π/6+cos²π/4+tan2π/3+cot2π/2
= ( 1/2)2 + (1 /√2)2 + (√32) + (0)2
= 1/4 + 1/2 + 3 =15/4
উদাহরণ ১৪.
7sin20+3cos20 = 4 হলে , প্রমান কর যে , tane = ± 1 √3
সমাধান:
দেওয়া আছে, 7sin 20 + 3cos 20 = 4
বা, 7sin20+3(1-sin20) = 4 [. sin20+ cos² = 1] ,
বা, 7sin20+3-3sin20= 4
বা, 4sin20 = 1
বা, sin20 = 1/4
cos²0 = 1-sin20
বা, tan20 = sin20/cos²0 = (1/4)/(3/4)
বা, tan20 = 1/3
বা,tan0 = 1 √3 (প্রমাণিত)।

উদাহরণ ১৫.
15cos20 + 2sin0 = 7 – 2 < 0 < হলে coti এর মান নির্ণয় কর।
সমাধান:
দেওয়া আছে, 15cos 20 + 2sin0 = 7
বা, 15(1-sin²0) + 2sine = 7 [. sin²0+ cos² = 1]
বা, 15-15sin20+2sin0=7
বা, 15sin20-2sin0-8=0
বা, 15sin20 – 12sin0+ 10sin0-8=0
বা, (3sin0 +2) (5sin-4)=0
বা, sin0= -2/3 বা, sin0 = 4 /5
বা, sine এর উভয় মান গ্রহণযোগ্য। কেননা – π/2<8 <π/2
sin0 = -2/3 হলে, cose = √(1-sin²0)
= √(1-4/9)
= √5/3
= √(1-16/25)
= 3/5
cot0= cos0/ sin0
= (√5/3)/(-2/3)
= – √5/2 [ sin0 = -2/3 হলে]
cot0 = cos0/ sin0
= (3/5)/(4/5)
=3/4 [ sin0 = 4 /5 হলে]
= নির্ণেয় মান – √5/2 বা, 3/4
উদাহরণ ১৬.
A = π/3 , B = π/6 হলে প্রমাণ কর যে,
ক) sin(A+B) sinAcosB+ cosAsinB =
খ) tan(A-B) = (tan A-tan B)/ (1+tan Atan B)
সমাধান :
ক) বামপক্ষ = sin(A + B) = sin(π/3 + π/6) =sin π/2 = 1
ডানপক্ষ sinAcos B + cos AsinB = sinπ/3 cosπ/6 + cosπ/3 sinπ/6
= (√3/2) .(√3/2)= (1/2). (1/2) = 3/4 + 1 /4= 1
বামপক্ষ = (প্রমাণিত)।
খ) tan(A-B) = (tan A-tan B)/ (1+tan Atan B)
বামপক্ষ = tan(A-B) = tan(π/3-π/6) = tanπ/6 = 1/√3
ডানপক্ষ = (tan A-tan B)/ (1+tan Atan B)
= (tanπ/3-tan π/6)/ (1+tan π/3tan π/6)
= { √3- (1/√3)}/{1+ √3 .1/√3}
= (2/√3).(1/2)
= 1/√3
বামপক্ষ = ডানপক্ষ (প্রমাণিত)।

১ thought on “ত্রিকোণমিতিক অনুপাতসমূহ ”