আজকে আমাদের আলোচনার বিষয়ঃ ত্রিভুজ ক্ষেত্রের ক্ষেত্রফল। এটি নবম – দশম শ্রেনী গণিতের পরিমিতি অংশের অন্তর্গত।

ত্রিভুজক্ষেত্রের ক্ষেত্রফল
পূর্বের শ্রেণিতে আমরা জেনেছি, ত্রিভুজ ক্ষেত্রের ক্ষেত্রফল = 1/2 × ভূমি × উচ্চতা
১. সমকোণী ত্রিভুজ:
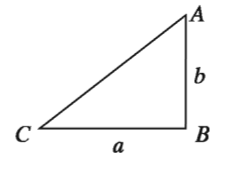
মনে করি, ABC সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহুদ্বয় যথাক্রমে BC = a এবং AB = b। BC কে ভূমি এবং AB কে উচ্চতা বিবেচনা করলে,
∆ABC এর ক্ষেত্রফল = 1/2 × ভূমি × উচ্চতা ।
২. ত্রিভুজ ক্ষেত্রের দুই বাহু ও এদের অন্তর্ভুক্ত কোণ দেওয়া আছে :
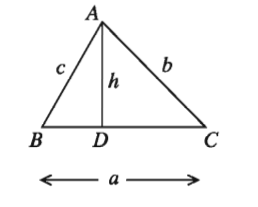
মনে করি, ABC ত্রিভুজের বাহুত্রয় BC = a, CA = b, AB = c । A থেকে BC বাহুর উপর AD লম্ব আঁকি। ধরি, উচ্চতা AD = h। কোণ C বিবেচনা করলে পাই, AD/CA = sinC
h/b = sinC বা, h = bsinC
∆ABC এর ক্ষেত্রফল = 1/2BC x AD
= 1/2a x bsinC = 1/2zab sinc
অনুরূপভাবে ∆ABC এর ক্ষেত্রফল
= 1/2bcsinA = 1/2casin B
৩.ত্রিভুজের তিন বাহু দেওয়া আছে :
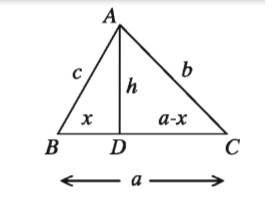
মনে করি, ∆ABC এর BC = a, CA = b এবং AB = c । এর পরিসীমা 2s = a+b+c । AD ⊥ BC আঁকি ।
ধরি, BD = x তাহলে, CD = a – x
∆ABD এবং ∆ACD সমকোণী।
AD2 = AB2 – BD2 এবং AD² = AC2 – CD2
AB2 – BD2 = AC2 – CD2
বা, c² – x²= b² (a-x)²
বা, c² – x²= b² – a²+2ax – x2
বা, 2ax = c²+a2-b2
x = (c² + a2-b²)/ 2a
আবার,
AD2 = c2-x2
= c2 – {(c² + a² – b²)/2a}²
= (c+ (c² + a² – b²)/2a) (c – (c² + a² – b²)/2a)
= (2ac + c² + a² – b2/2a).( 2ac- c²-a2+b²/2a)
= {(c + a)² – b²} {b² – (c − a)²}/4a2
= {(c+a+b)(c+a- b) (b + c − a) (b − c + a)}/4a2
= {(a+b+c)(a+b+c − 2b) (a + b + c − 2a) (a+b+c−2c)} /4a2
= {2s(2s – 2b)(2s – 2a)(2s – 2c)} /4a2
= (4s(s – a)(s – b)(s—c))/ a2
AD = 2/a√s(s − a)(s — b)(s – c)
∆ABC এর ক্ষেত্রফল
= 1/2 BC. AD = 1/2 . а 2/a √s(s − a)(s — b)( s − c) = √s( s − a)(s — b)(s — c)
৪. সমবাহু ত্রিভুজ:
মনে করি, ABC সমবাহু ত্রিভুজের প্রত্যেক বাহুর দৈর্ঘ্য a
AD⊥BC আঁকি। BD = CD= a/2
∆ABD সমকোণী ।
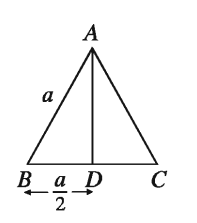
BD2+ AD2 = AB2
বা, AD2 = AB² – BD² = a² — (a/2)² = a² – a²/4 = 3a2/4
AD = √3a/2
∆ABC এর ক্ষেত্রফল = 1/2BC. AD = 1/2.a.√3a/2 = √3/4a2
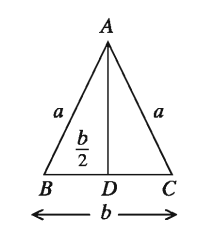
৫. সমদ্বিবাহু ত্রিভুজ :
মনে করি, ABC সমদ্বিবাহু ত্রিভুজের
AB = AC = a BC = b
AD⊥BC আঁকি। BD = CD =b/2
∆ABD সমকোণী।
AD2 = AB2 – BD2
=a²- (b/2)² = a² – b²/4 = (4a² -b²)/4
AD = √(4a2-b2)/ 2
সমদ্বিবাহু ∆ABC এর ক্ষেত্রফল BC. AD = 2
=1/2.b. (√4a2 – b2)/2 = b/4√(4a² -b²)
উদাহরণ ১.
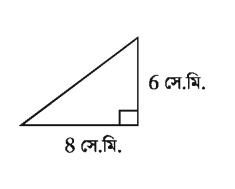
একটি সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহুদ্বয়ের দৈর্ঘ্য যথাক্রমে 6 সে.মি. ও ৪ সে.মি. হলে এর ক্ষেত্রফল নির্ণয় কর।
সমাধান:
মনে করি, সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহুদ্বয় যথাক্রমে a = 6 সে.মি. এবং b = ৪ সে.মি.।
এর ক্ষেত্রফল = 1/2ab = 1/2 × 6 × ৪ বর্গ সে.মি. = 24 বর্গ সে.মি.।
উদাহরণ ২.
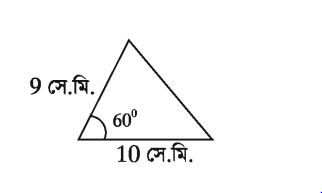
কোনো ত্রিভুজের দুই বাহুর দৈর্ঘ্য যথক্রমে 9 সে.মি. ও 10 সে.মি. এবং এদের অন্তর্ভুক্ত কোণ 60° । ত্রিভুজটির ক্ষেত্রফল নির্ণয় কর।
সমাধান:
মনে করি, ত্রিভুজের বাহুদ্বয় যথাক্রমে a = 9 সে.মি. ও b = 10 সে.মি. এবং এদের অন্তর্ভুক্ত কোণ ৪ = 60°।
:: ত্রিভুজটির ক্ষেত্রফল = 1/2absin60°
= 1/2 × 9 × 10 × √3/2 বর্গ সে.মি. = 38.97 বর্গ সে.মি. (প্রায়)
নির্ণেয় ক্ষেত্রফল 38.97 বর্গ সে.মি. (প্রায়)
উদাহরণ ৩.
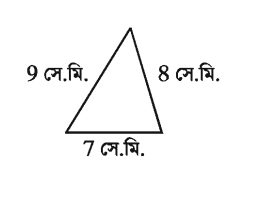
একটি ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য যথাক্রমে 7 সে.মি., ৪ সে.মি. ও 9 সে.মি.। এর ক্ষেত্রফল নির্ণয় কর।
সমাধান:
মনে করি, ত্রিভুজটির বাহুগুলোর দৈর্ঘ্য যথাক্রমে a = 7 সে.মি., b = ৪ সে.মি. ও c = 9 সে.মি. ।
অর্ধপরিসীমা s = (a+b+c) /2 = (7+8+9)/2সে.মি. = 12 সে.মি.
ত্রিভুজের ক্ষেত্রফল √{s ( s – a) (s – b) (s-c)}
= √{12 (127) (128) (12 – 9)} বর্গ সে.মি.
= √(12 x 5 x 4 x 3) বর্গ সে.মি.
= √720 = 26.83 বর্গ সে.মি. (প্রায়)
ত্রিভুজটির ক্ষেত্রফল 26.83 বর্গ সে.মি. (প্রায়)
উদাহরণ ৪.
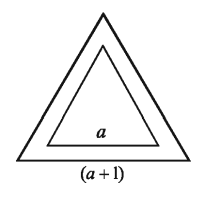
একটি সমবাহু ত্রিভুজের প্রত্যেক বাহুর দৈর্ঘ্য 1 মিটার বাড়ালে ক্ষেত্রফল 3√3 বর্গমিটার বেড়ে যায়। ত্রিভুজটির বাহুর দৈর্ঘ্য নির্ণয় কর।
সমাধান :
মনে করি, সমবাহু ত্রিভুজের প্রত্যেক বাহুর দৈর্ঘ্য a মিটার।
ত্রিভুজটির ক্ষেত্রফল = √3/4a2 বর্গমিটার।
ত্রিভুজটির প্রত্যেক বাহুর দৈর্ঘ্য 1 মিটার বাড়ালে ত্রিভুজটির ক্ষেত্রফল √3 /4 (a + 1)2 বর্গমিটার।
প্রশ্নানুসারে, √3 /4(a + 1)2 – √3 /4a2 = 3√3
বা, (a + 1 ) 2 – a2 = 12 [√3 /4 দ্বারা ভাগ করে]
বা, a2 + 2a + 1 – a2 = 12 বা, 2a = 11 বা, a = 5.5
নির্ণেয় বাহুর দৈর্ঘ্য 5.5 মিটার।
উদাহরণ ৫.
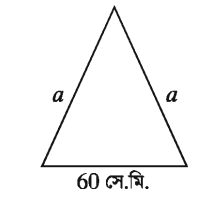
একটি সমদ্বিবাহু ত্রিভুজের ভূমির দৈর্ঘ্য 60 সে.মি.। এর ক্ষেত্রফল 1200 বর্গ সে.মি. হলে সমান সমান বাহুর দৈর্ঘ্য নির্ণয় কর।
সমাধান: মনে করি, সমদ্বিবাহু ত্রিভুজের ভূমি b = 60 সে.মি. এবং সমান সমান বাহুর দৈর্ঘ্য a.
ত্রিভুজটির ক্ষেত্রফল b/4√4a2-b2
প্রশ্নানুসারে, b/4√4a2-b2 = 1200
বা, 60/4√{4a² -(60)²}= 1200
বা, 15√{4a² – 3600} = 1200
বা, √4a2 – 3600 = 80
বা, 4a2 – 3600 = 6400 [বর্গ করে]
বা, 4a2 = 10000
বা, a2 = 2500
a = 50
ত্রিভুজটির সমান বাহুর দৈর্ঘ্য 50 সে.মি.।
উদাহরণ ৬.
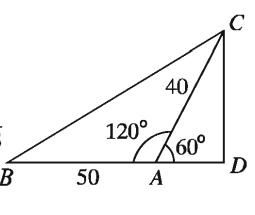
একটি নির্দিষ্ট স্থান থেকে দুইটি রাস্তা 120° কোণে চলে গেছে। দুই জন লোক ঐ নির্দিষ্ট স্থান থেকে যথাক্রমে ঘণ্টায় 10 কিলোমিটার ও ৪ ঘণ্টায় কিলোমিটার বেগে বিপরীত দিকে রওনা হলো। 5 ঘণ্টা পরে তাদের মধ্যে সরাসরি দূরত্ব নির্ণয় কর।
সমাধান:
মনে করি, A স্থান থেকে দুইজন লোক যথাক্রমে ঘণ্টায় 10 কিলোমিটার ও ঘণ্টায় ৪ কিলোমিটার বেগে রওনা হয়ে 5 ঘণ্টা পর যথাক্রমে B ও C স্থাণে পৌঁছালো। তাহলে, 5 ঘণ্টা পর তাদের মধ্যে সরাসরি দূরত্ব হবে BCC থেকে BA এর বর্ধিতাংশের উপর CD লম্ব টানি।
AB= 5 × 10 কিলোমিটার = 50 কিলোমিটার, AC = 5 x 8 কিলোমিটার = 40 কিলোমিটার এবং ∠BAC = 120°
∠DAC = 180° – 120° = 60°
∆ACD সমকোণী।
CD/AC = sin 60° বা, CD = ACsin 60° = 40 x √3/2 = 20√3
এবং AD/AC = cos 60° বা, AD = ACcos 60° 40 x 1/= 20
আবার, সমকোণী ত্রিভুজ BCD থেকে পাই,
BC2 = BD 2 + CD 2 = (BA + AD) 2 + CD 2
= (50+20)² + (20√3)2 = 4900+1200 = 6100
BC = 78.1 (প্রায়)
নির্ণেয় দূরত্ব 78.1 কিলোমিটার (প্রায়)
উদাহরণ ৭.
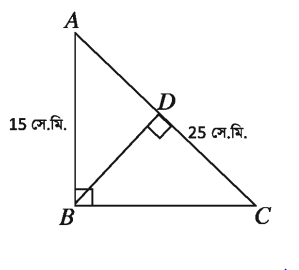
প্রদত্ত চিত্রের আলোকে
ক) BC বাহুর দৈর্ঘ্য নির্ণয় কর।
খ) BD এর মান নির্ণয় কর।
গ) ∆ABD ও ∆BCD এর ক্ষেত্রফলদ্বয়ের অনুপাত নির্ণয় কর।
সমাধান :
ক) AB = 15, AC = 25
BC = √(AC2 – AB2) = √{(25)-(15)2} = √400 = 20
খ) ∆ABC এর ক্ষেত্রফল = 1/2 BC. AB = 1/2 AC. BD
1/2AC.BD = 1/2BC.AB
25 x BD = 20 x 15
.:. BD = 12
গ) ∆ABD সমকোণী থেকে পাই AD2 + BD2 = AB2
বা, AD2 + 122 = 152
বা, AD2 = 225 – 144 = 81
বা, AD=9 এবং CD = AC-AD = 25-9 = 16
অতএব, ∆ABD ও ∆BCD এর ক্ষেত্রফলদ্বয়ের অনুপাত,
∆ABD/∆BCD = (1/2 BD. AD)/(1/2 BD.CD) = 9/16
∆ABD: ∆BCD = 9: 16
