ত্রিভুজ সংক্রান্ত কতিপয় সম্পাদ্য

আজকে আমরা  ত্রিভুজ সংক্রান্ত কতিপয় সম্পাদ্য সম্পর্কে  আলোচনা করবো । যা উচ্চতর গণিতের জ্যামিতিক অঙ্কন অংশের অন্তর্গত।

 

 

ত্রিভুজ সংক্রান্ত কতিপয় সম্পাদ্য

সম্পাদ্য ১.

ত্রিভুজের ভূমি, ভূমি সংলগ্ন একটি কোণ ও উচ্চতা দেওয়া আছে, ত্রিভুজটি অঙ্কন কর।

 

 

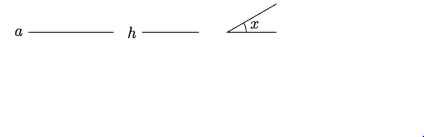
মনে করি, কোনো ত্রিভুজের ভূমি a, উচ্চতা h এবং ভূমি সংলগ্ন একটি কোণ x দেওয়া আছে। ত্রিভুজটি অঙ্কন করতে হবে।

অঙ্কন:

ধাপ ১.

যেকোনো রেখা BD থেকে BC = a অংশ কেটে নিই।

 

 

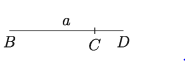
ধাপ ২.

B বিন্দুতে BC এর উপর লম্ব BP আঁকি। BP থেকে BM = h কেটে নিই

 

 

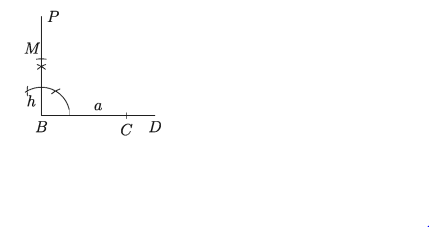
ধাপ ৩.

M বিন্দুতে MN || BC অঙ্কন করি।

 

 

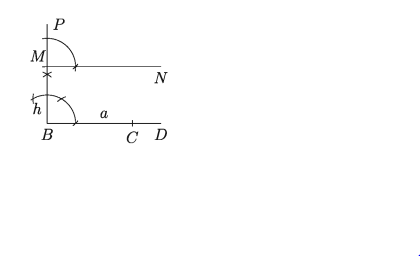
ধাপ ৪.

আবার B বিন্দুতে প্রদত্ত ∠x এর সমান করে ∠CBE অঙ্কন করি। BE রেখাংশ MN কে A বিন্দুতে ছেদ করে।

 

 

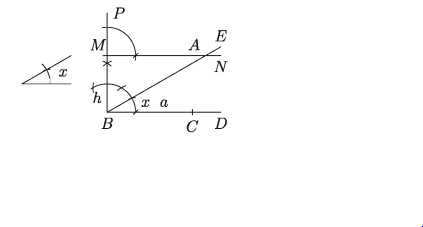
ধাপ ৫.

A, C যোগ করি। তাহলে ABC-ই  উদ্দিষ্ট ত্রিভুজ।

 

 

 

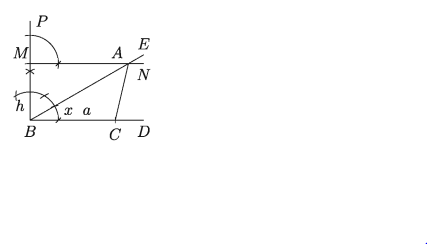
প্ৰমাণ:

MN || BC (অঙ্কনানুসারে)। . ABC এর উচ্চতা BM = = h। আবার, BC = a এবং∠ABC = ∠x। ∆ABC-ই উদ্দিষ্ট ত্রিভুজ।

বিশ্লেষণ:

ভূমি ও ভূমি সংলগ্ন কোণ দেয়া আছে। সুতরাং একটি সরলরেখা থেকে ভূমির সমান অংশ কেটে নিয়ে তার এক প্রান্তে প্রদত্ত কোণের সমান কোণ আঁকতে হবে। অতঃপর ভূমির সঙ্গে নির্দিষ্ট কোণে আনত নতুন অঙ্কিত রেখার উপর এমন একটা বিন্দু নির্ণয় করতে হবে যেন ভূমি থেকে ঐ বিন্দুটির উচ্চতা ত্রিভুজের উচ্চতার সমান হয়

সম্পাদ্য ২.

ত্রিভুজের ভূমি, শিরঃকোণ ও অপর বাহুদ্বয়ের সমষ্টি দেওয়া আছে। ত্রিভুজটি অঙ্কন কর ।

মনে করি, একটি ত্রিভুজের ভূমি a, অপর বাহুদ্বয়ের সমষ্টি s এবং শিরঃকোণ দেওয়া আছে। ত্রিভুজটি অঙ্কন করতে হবে।

 

 

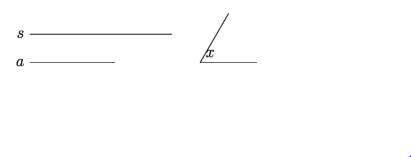
অঙ্কন:

ধাপ ১.

যেকোনো রেখা DE থেকে DB = s অংশ কেটে নিই।

 

 

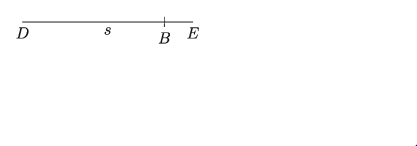
ধাপ ২.

DB রেখার D বিন্দুতে ∠BDF = 1/2∠Zx অঙ্কন করি।

 

 

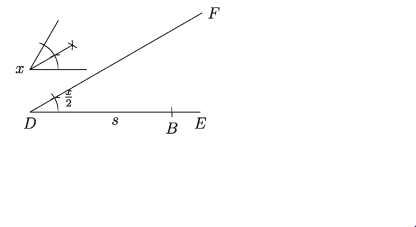
ধাপ ৩.

B কে কেন্দ্র করে ভূমি a এর সমান ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ অঙ্কন করি যা DF’ কে C ও C’ বিন্দুতে ছেদ করে। B,C ও B,C’ যোগ করি।

রেখা দুইটি BD কে যথাক্রমে A ও A’ বিন্দুতে ছেদ করে। তাহলে ABC ও A’BC’ ত্রিভুজদ্বয় উদিষ্ট ত্রিভুজ।

 

 

 

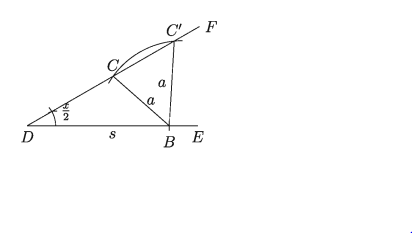
ধাপ ৪.

C বিন্দুতে ZBDF এর সমান ∠DCA ও C’ বিন্দুতে ZBDF এর সমান ∠DC’A’ অঙ্কন করি। CA ও C ‘A’

 

 

প্রমাণ:

যেহেতু ∠ACD = ∠ADC = ∠A’C’D =1/2 ∠x (অঙ্কনানুসারে)

∠BAC = ∠ADC + ∠ACD =1/2∠x+1/2x = x

∠BA’C’ = ∠A’DC’ + ∠A’C’ D  = 1/2∠x+1/2x = x

এবং AC = AD, A’C’ = A’D

ABC ত্রিভুজে

∠BAC = ∠x, BC = a এবং CA + AB = DA + AB = DB = s

.: AABC-ই উদ্দিষ্ট ত্রিভুজ।

আবার A’BC’ ত্রিভুজে,

∠BA’C’ = ∠x, BC’ : = a এবং C’A’ + A’B = DA’ + A’B = DB = s

A’BC’-ই অপর উদ্দিষ্ট ত্রিভুজ।

সম্পাদ্য ৩.

ত্রিভুজের ভূমি, শিরঃকোণ ও অপর দুই বাহুর অন্তর দেওয়া আছে। ত্রিভুজটি অঙ্কন কর ।

 

 

 

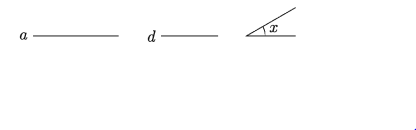
মনে করি, একটি ত্রিভুজের ভূমি a, অপর দুই বাহুর অন্তর d এবং শিরঃকোণ x দেওয়া আছে। ত্রিভুজটি অঙ্কন করতে হবে।

 

 

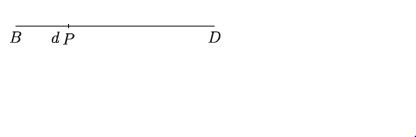
অঙ্কন:

ধাপ ১.

যেকোনো রেখা BD_থেকে_BP = d অংশ কেটে নিই।

ধাপ ২.

P বিন্দুতে ∠x এর সম্পূরক কোণের অর্ধেকের সমান ∠DPM অঙ্কন করি।

 

 

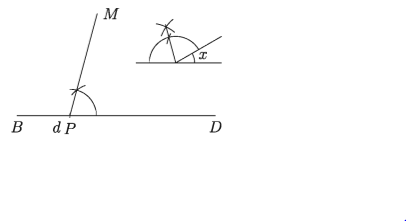
ধাপ ৩.

B কে কেন্দ্র করে এর সমান ব্যাসার্ধ নিয়ে অঙ্কিত বৃত্তচাপ PM সরলরেখাকে C বিন্দুতে ছেদ করে। B ও C যোগ করি।

 

 

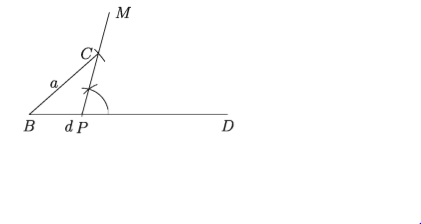
ধাপ ৪.

আবার C বিন্দুতে ∠DPC = ∠PCA কোণ অঙ্কন করি যেন CA রেখাংশ BD কে A বিন্দুতে ছেদ করে। তাহলে ABC-ই উদ্দিষ্ট ত্রিভুজ।

 

 

প্রমাণ:

∠APC = ∠ACP

AP =  AC

AB – AC = AB – AP = d

আবার ∠APC = ∠ACP = ∠x এর সম্পূরক কোণের অর্ধেক।

∠APC + ∠ACP = ∠x এর সম্পূরক = বহিঃস্থ ∠CAD = ∠CAB এর সম্পূরক।

∠A = ∠CAB = ∠a

ABC-ই নির্ণেয় ত্রিভুজ।

সম্পাদ্য ৪.

ত্রিভুজের উচ্চতা, ভূমির উপর মধ্যমা এবং ভূমি সংলগ্ন একটি কোণ দেওয়া আছে। ত্রিভুজটি অঙ্কন করতে হবে।

 

 

মনে করি, ত্রিভুজের উচ্চতা h, ভূমির ওপর মধ্যমা d এবং ভূমি সংলগ্ন একটি Zx দেওয়া আছে। ত্রিভুজটি অঙ্কন করতে হবে।

 

 

 

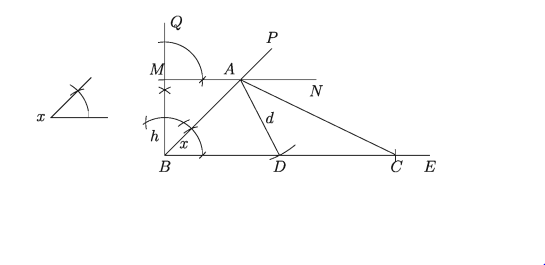
অঙ্কন :

ধাপ ১.

যেকোনো রেখা BE এর B বিন্দুতে Zx এর সমান ZEBP অঙ্কন করি।

ধাপ ২.

B বিন্দুতে BE রেখার ওপর BQ লম্ব অঙ্কন করি।

ধাপ ৩.

BQ থেকে ত্রিভুজের উচ্চতা । এর সমান BM অংশ কেটে নিই।

ধাপ ৪.

M বিন্দুতে MN || BE অঙ্কন করি যা BP কে A বিন্দুতে ছেদ করে।

ধাপ ৫.

A বিন্দুকে কেন্দ্র করে মধ্যমা d এর সমান ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ অঙ্কন করি BE কে D বিন্দুতে ছেদ করে।

ধাপ ৬.

BE থেকে DC = BD অংশ কেটে নিই। A ও C যোগ করি ।
তাহলে, AABC-ই উদ্দিষ্ট ত্রিভুজ।

প্রমাণ:

BD = DC, D বিন্দুই BC এর মধ্যবিন্দু।

A, D যোগ করি।

AD = d = ভূমির উপর অঙ্কিত মধ্যমা, অর্থাৎ, BC ভূমি।
MN ও BE সমান্তরাল।

সুতরাং AABC এর উচ্চতা BM = h।

আবার, ∠ABC = 2x = ভূমি সংলগ্ন একটি কোণ।
.: ABC-ই উদ্দিষ্ট ত্রিভুজ।

মন্তব্য:

∠r এর উপর নির্ভর করে অনেক ক্ষেত্রে দুইটি ত্রিভুজ পাওয়া যেতে পারে। এছাড়াও মধ্যমার দৈর্ঘ্য উচ্চতার থেকে কম হলে অঙ্কন করা যাবে না।

উদাহরণ ১.

ত্রিভুজের ভূমির দৈর্ঘ্য 5 সে.মি., ভূমি সংলগ্ন কোণ 60° এবং অপর দুই বাহুর সমষ্টি 7 সে.মি.। ত্রিভুজটি অঙ্কন করতে হবে।

সমাধান:

দেওয়া আছে ভূমি BC = 5 সে.মি. অপর দুই বাহুর সমষ্টি AB + AC = 7 সে.মি. এবং ∠ABC = 60°। ABC অঙ্কন করতে হবে।

 

ধাপ ১

যেকোনো রেখা BX থেকে BC 5 সে.মি. কেটে নিই।

ধাপ ২.

∠X BY = 60° আঁকি।

ধাপ ৩.

BY রেখা থেকে BD = 7 সে.মি, কেটে নিই।

ধাপ ৪.

C, D যোগ করি।

ধাপ ৫.

CD রেখার লম্বদ্বিখন্ডক আঁকি যা BD কে A বিন্দুতে ছেদ করে।

ধাপ ৬.

A,C যোগ করি, তাহলে ABC-ই নির্ণেয় ত্রিভুজ।

 

 

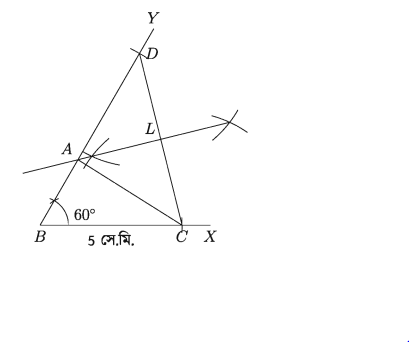
দ্রষ্টব্য:

যেহেতু AL, CD এর লম্বদ্বিখণ্ডক, AD = AC

তাহলে BD = BA + AD = BA + AC = 7 সে.মি.।

উদাহরণ ২.

ত্রিভুজের ভূমির দৈর্ঘ্য 7.5 সে.মি. ভূমি সংলগ্ন কোণ 45° এবং অপর দুই বাহুর অন্তর 2.5 সে.মি. দেওয়া আছে। ত্রিভুজটি অঙ্কন করতে হবে।

সমাধান:

দেওয়া আছে ভূমি BC = 7.5 সে.মি, অপর দুই বাহুর অন্তর AB – AC বা AC – AB = 2.5 সে.মি. এবং ভূমি সংলগ্ন কোণ 45°। ত্রিভুজটি আঁকতে হবে। আমরা এখানে AB AC = 2.5 সে.মি. এর ক্ষেত্রে অঙ্কনের ধাপসমূহ দেখবো। [ACAB 2.5 সে.মি. ধরে ত্রিভুজটি নিজে অঙ্কন কর।]

 

 

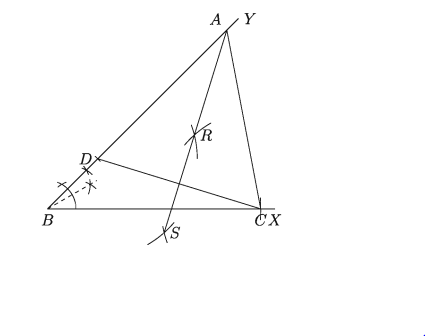
ধাপ ১.

যেকোনো রেখা BX থেকে BC = 7.5 সে.মি. কেটে নিই।

ধাপ ২.

ZY BC = 45° অঙ্কন করি।

ধাপ ৩.

BY রেখা থেকে BD = 2.5 সে.মি. কেটে নিই।

ধাপ ৪.

C, D যোগ করি।

ধাপ ৫.

CD এর ওপর RS লম্বদ্বিখণ্ডক আঁকি যেন BY কে A বিন্দুতে ছেদ করে।

ধাপ ৬.

A ও C যোগ করি। তাহলে ABC-ই নির্ণেয় ত্রিভুজ।