আজকে আমরা স্থানাঙ্ক জ্যামিতির দুইটি বিন্দুর মধ্যবর্তী দূরত্ব সম্পর্কে আলোচনা করবো । যা উচ্চতর গণিতের স্থানাঙ্ক জ্যামিতি অংশের অন্তর্গত।

স্থানাঙ্ক জ্যামিতির দুইটি বিন্দুর মধ্যবর্তী দূরত্ব
মনে করি, P(x1,y1) এবং Q(x2, Y2) একটি সমতলে অবস্থিত দুইটি ভিন্ন বিন্দু। P ও Q বিন্দু থেকে x অক্ষের উপর লম্ব PM ও QN আঁকি। আবার P বিন্দু থেকে QN এর উপর লম্ব PR আঁকি।
এখন P বিন্দুর ভুজ = OM = x1 এবং P বিন্দুর কোটি = MP = Y1 | Q বিন্দুর ভুজ = ON = x2 ও কোটি NQ = y2 । চিত্র হতে আমরা পাই,
PR = MN = ON – OM = x2 – x1
QR = NQ – NR = NQ – MP = y2 – y1

অঙ্কন অনুসারে, PQR একটি সমকোণী ত্রিভুজ এবং PQ ত্রিভুজের অতিভুজ। তাই পীথাগোরাসের উপপাদ্য অনুযায়ী
PQ2 = PR2 + QR2
বা, PQ = ±√(PR2 + QR2)
বা, PQ = ±√{(x2 – x1 ) 2 + (y2 – y1 ) 2 }
P বিন্দু হতে Q বিন্দুর দূরত্ব, PQ = {(x2 – x1 ) 2 + (y2 – y1 ) 2 }
যেহেতু দূরত্ব সবসময় অঋণাত্মক হয় সেহেতু ঋণাত্মক মান পরিহার করা হয়েছে।
আবার একই নিয়মে Q বিন্দু হতে P বিন্দুর দূরত্ব,
QP = √{(x1- x2)² + (y1 — y2)²} = √{(x2 – x1 ) 2 + (y2 – y1 ) 2 }
∴ PQ = QP
P বিন্দু হতে Q বিন্দু বা Q বিন্দু হতে P বিন্দুর দূরত্ব সমান।
অর্থাৎ PQ = √{(x2 – x1 ) 2 + (y2 – y1 ) 2 } = QP
অনুসিদ্ধান্ত ১.
মূলবিন্দু (0,0) হতে সমতলে অবস্থিত যেকোনো বিন্দু P(x, y) এর দূরত্ব
PQ = √{(x – 0)2 + (y – 0) 2} = √(x2 + y2)
উদাহরণ ১.
(1,1) এবং (2,2) বিন্দু দুইটি একটি সমতলে চিহ্নিত কর। এদের মধ্যবর্তী দূরত্ব নির্ণয় কর।
সমাধান:
ধরি, P(1,1) এবং Q (2,2) প্রদত্ত বিন্দুদ্বয়। চিত্রে, xy সমতলে বিন্দুদ্বয়কে চিহ্নিত করা হলো।
বিন্দুদ্বয়ের মধ্যবর্তী দূরত্ব,
PQ = √{(x2 – x1 ) 2 + (y2 – y1 ) 2 }
= √{(2 − 1)² + (2 − 1)²}
= √(1²+1²)
= √(1 + 1)
= √2

উদাহরণ ২.
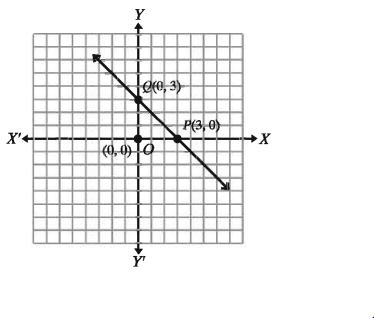
মূলবিন্দু O(0, 0) এবং অপর দুইটি বিন্দু P (3,0) ও Q (0, 3) সমতলে চিহ্নিত কর। প্রত্যেকের মধ্যবর্তী দূরত্ব নির্ণয় কর। তিনটি বিন্দু যোগ করলে যে জ্যামিতিক চিত্র অঙ্কিত হয় তার নাম কি এবং কেন?
সমাধান:
বিন্দু তিনটির অবস্থান সমতলে দেখানো হলো ।
দূরত্ব OP = √{(3 – 0 ) 2 + (0 – 0 ) 2}
= √(32 +0²)
= √32
= 3 একক
দূরত্ব 0Q = √{ (0 – 0 ) 2 + ( 3 – 0 ) 2}
= √(02 +32)
= √ 32
= 3 একক
দূরত্ব PQ = √{(3 – 0 ) 2 + (0 – 3 ) 2}
= √(9+9)
= √18
= 3√2 একক
জ্যামিতিক চিত্রটির নাম সমদ্বিবাহু ত্রিভুজ কারণ এর দুই বাহু OP এবং OQ এর দৈর্ঘ্য সমান।
উদাহরণ ৩.
একটি ত্রিভুজের তিনটি শীর্ষবিন্দু যথাক্রমে A ( 2,0), B(70) ও C(3,4)। সমতলে এদের অবস্থান দেখাও এবং ত্রিভুজটি অঙ্কন কর। ত্রিভুজটির পরিসীমা পাঁচ দশমিক স্থান পর্যন্ত নির্ণয় কর।
সমাধান:
xy সমতলে A ( 2,0 ), B(7, 0 ) ও C (3, 4 ) এর অবস্থান দেখানো হলো। ABC ত্রিভুজের,
AB বাহুর দৈর্ঘ্য = √{(7 – 2 ) 2 + (0 – 0 ) 2}
= √52
= 5 একক
BC বাহুর দৈর্ঘ্য = √{(3 – 7)2 + (4- 0)2}
= √{(-4)2 + 42}
= √16 + 16
= 4√2 একক
AC বাহুর দৈর্ঘ্য = √{(3-2)²+(4-0)2}
= √(1² +4²)
= √17 একক
ত্রিভুজটির পরিসীমা = (AB + BC + AC )
[বাহুত্রয়ের দৈর্ঘ্যের সমষ্টি]
= (5 + 4√2 + √17) একক = 14.77996 একক (প্রায়)

উদাহরণ ৪.
দেখাও যে, (0, −1), (2, 3), (6, 7 ) এবং (8, 3) বিন্দুগুলো একটি আয়তক্ষেত্রের চারটি শীর্ষবিন্দু।
সমাধান:
মনে করি, A(0, – 1), B(-2, 3), C(6, 7) এবং D(8,3) প্রদত্ত বিন্দুসমূহ। xy সমতলে এদের অবস্থান দেখানো হলো।
AB বাহুর দৈর্ঘ্য = √{(-2-0)2 + (3 − (−1))²}
= √{(-2)2 + (4)2}
= √4 + 16
= 2√5 একক
CD বাহুর দৈর্ঘ্য = √ {(8 – 6 ) 2 + ( 37 ) 2}
= √(4 + 16)
= 2/5 একক
AB বাহুর দৈর্ঘ্য = CD বাহুর দৈর্ঘ্য
আবার,
AD বাহুর দৈর্ঘ্য = √{(8-0)² + (3 − (−1))²}
= √(82 + 42)
= √80 = 4√5 একক
BC বাহুর দৈর্ঘ্য = √{6-(-2))²+(7–3)2}
= √(8² + 4²)
= √80
= 4√5 একক
AD বাহুর দৈর্ঘ্য = BC বাহুর দৈর্ঘ্য
∴ বিপরীত বাহুগুলোর দৈর্ঘ্য সমান।
সুতরাং বলা যায়, ABCD একটি সামান্তরিক।
BD কর্ণের দৈর্ঘ্য = √{(8 – (-2))2 + (3 – 3)2}
= √ 10² + (0)² = √ 100
= 10 একক
এখন, BD² = 100, AB² = ( 2/5 )² = 20, AD² = ( 4/5 )² = 80
AB² + AD² = 20 + 80 = 100 = BD²
পীথাগোরাসের উপপাদ্য অনুযায়ী ABD একটি সমকোণী ত্রিভুজ এবং ∠BAD সমকোণ। সুতরাং এ দ্বারা প্রমাণিত হলো যে, ∆BCD একটি আয়তক্ষেত্র।

উদাহরণ ৫.
দেখাও যে, (−3, −3), (0, 0 ) ও ( 3, 3 ) বিন্দু তিনটি দ্বারা কোনো ত্রিভুজ তৈরি করা যায় না।
সমাধান:
ধরি, A(−3, – 3), B(0, 0 ) ও C (3,3) প্রদত্ত বিন্দুসমূহ। y সমতলে তাদের অবস্থান দেখানো হলো।
আমরা জানি, যেকোনো ত্রিভুজের দুই বাহুর সমষ্টি তৃতীয় বাহু অপেক্ষা বড়। ধরে নিই ABC একটি ত্রিভুজ এবং AB, BC ও AC এর তিনটি বাহু।
AB বাহুর দৈর্ঘ্য = √{0 – (-3))2 + (0 – (-3))2}
= √32 + 32
= √18
= 3√2 একক
BC বাহুর দৈর্ঘ্য = √{(3-0)2 + (3-0)2}
= √32 + 32
= √18
= 3√2 একক
AC বাহুর দৈর্ঘ্য = √ {(3 + 3)2 + ( 3 + 3)2}
= √72
= 6√2 একক
সুতরাং AB + BC = 3√2 + 3√2 = 6√2 = AC
অর্থাৎ দুই বাহুর সমষ্টি তৃতীয় বাহুর সমান। সুতরাং এদের দ্বারা কোনো ত্রিভুজ গঠন সম্ভব নয়।

আবার xy সমতলে অবস্থান দেখে বলা যায় যে বিন্দু তিনটি একই সরলরেখায় অবস্থান করে এবং এদের দ্বারা কোনো ত্রিভুজ গঠন সম্ভব নয়।

১ thought on “স্থানাঙ্ক জ্যামিতির দুইটি বিন্দুর মধ্যবর্তী দূরত্ব ”