দ্বিঘাত সমীকরণের ব্যবহার

আজকে আমাদের আলোচনার বিষয়ঃ দ্বিঘাত সমীকরণের ব্যবহার। এটি নবম – দশম শ্রেনী গণিতের এক চলকবিশিষ্ট সমীকরণ এর অন্তর্গত।

 

 

দ্বিঘাত সমীকরণের ব্যবহার

আমাদের দৈনন্দিন জীবনের অনেক সমস্যা এক চলকবিশিষ্ট একঘাত সমীকরণ ও দ্বিঘাত সমীকরণে রূপান্তর করে সহজে সমাধান করা যায়। এখানে, বাস্তবভিত্তিক সমস্যায় প্রদত্ত শর্ত থেকে দ্বিঘাত সমীকরণ গঠন করে সমাধান করার কৌশল দেখানো হলো।

 

 

 

উদাহরণ ১২.

একটি প্রকৃত ভগ্নাংশের হর, লব অপেক্ষা 4 বেশি। ভগ্নাংশটি বর্গ করলে যে ভগ্নাংশ পাওয়া যাবে তার হর, লব অপেক্ষা 40 বেশি হবে। ভগ্নাংশটি নির্ণয় কর ।

সমাধান:

ধরি, ভগ্নাংশটির লব x এবং হর x + 4

সুতরাং ভগ্নাংশটি x /(x + 4 )

ভগ্নাংশটির বর্গ  {x /(x + 4 )} 2 = x2/(x + 4 )2 = x2/x2 + 8x + 16

এখানে, লব = x2 এবং হর = x2 +8x + 16

প্রশ্নমতে, x2 +8x + 16 = x2 + 40

বা, 8x + 16 = 40

বা, x = 40 – 16

বা, 8x = 24

বা, x = 3

x+4 = 3+4=7

x /(x + 4 ) = 3/7

ভগ্নাংশটি 3/7

উদাহরণ ১৩.

50 মিটার দৈর্ঘ্য এবং 40 মিটার প্রস্থবিশিষ্ট একটি আয়তাকার বাগানের ভিতরের চারদিকে সমান চওড়া একটি রাস্তা আছে। রাস্তা বাদে বাগানের ক্ষেত্রফল 1200 বর্গমিটার হলে, রাস্তাটি কত মিটার চওড়া?

 

 

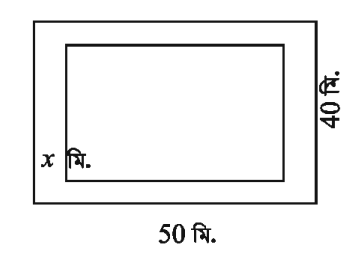
সমাধান:

মনে করি, রাস্তাটি x মিটার চওড়া।

রাস্তা বাদে বাগানটির দৈর্ঘ্য (50 – 2x ) মিটার এবং প্রস্থ ( 40 – 2x ) মিটার

রাস্তা বাদে বাগানটির ক্ষেত্রফল = (50 – 2x) × (40 – 2x) বর্গমিটার।

প্রশ্নমতে, ( 50 – 2x ) x ( 40 – 2x ) = 1200

বা, 2000 – 80x – 100x + 4×2 = 1200

বা, 4x 2 – 180x + 800 = 0

বা, x2 – 45x + 200 = 0 [4 দিয়ে ভাগ করে ]

বা, x2 – 5x – 40x + 200 = 0

বা, x(x – 5 ) – 40 (x – 5) = 0

বা, (x – 5) (x – 40 ) = 0

x – 5 = 0 অথবা x – 40 = 0

x – 5 = 0 হলে, x = 5

x – 40 = 0 হলে, x = 40

কিন্তু রাস্তাটি বাগানটির প্রস্থ 40 মিটার থেকে কম চওড়া হবে।

x ≠ 40; x=5

রাস্তাটি 5 মিটার চওড়া।

 

উদাহরণ ১৪.

শাহিক 240 টাকায় কতগুলো কলম কিনল। সে যদি ঐ টাকায় একটি কলম বেশি পেতো তবে প্রতিটি কলমের দাম গড়ে 1 টাকা কম পড়তো। সে কতগুলো কলম কিনল?

সমাধান:

মনে করি, শাহিক 240 টাকায় মোট টি কলম কিনেছিল। এতে প্রতিটি কলমের দাম পড়ে 240/x টাকা ।

সে যদি 240 টাকায় (x + 1) টি কলম পেতো তবে প্রতিটি কলমের দাম পড়তো 240/( x + 1) টাকা।

প্রশ্নমতে, 240/( x + 1) = 240/x – 1

বা, 240/( x + 1) = (240-x)/x

বা, 240x=(x+1)(240 – x) [আড়গুণন করে]

বা, 240x = 240x + 240 – x2 – x

বা, x2 + x – 240 = 0 [পক্ষান্তর করে]

বা, x²+16x – 15x-240 = 0

বা, x(x+16) – 15(x+16) = 0

বা, (x+16)(x − 15) = 0

x+16 = 0, অথবা  x-15=0

x+16= 0 হলে, x = -16

x -15 = 0, x = 15

কিন্তু কলমের সংখ্যা এক্স ঋণাত্মক হতে পারে না।

x ≠ -16; x = 15

শাহিক 15 টি কলম কিনেছিল।

 

 

উদাহরণ ১৫.

একটি বিদ্যালয়ের নবম শ্রেণির একটি পরীক্ষায় x জন ছাত্রের গণিতে প্রাপ্ত মোট নম্বর 1950। একই পরীক্ষায় অন্য একজন নতুন ছাত্রের গণিতে প্রাপ্ত নম্বর 34 যোগ করায় প্রাপ্ত নম্বরের গড় 1 কমে গেল ।

ক) পৃথকভাবে x জন ছাত্রের এবং নতুন ছাত্রসহ সকলের প্রাপ্ত নম্বরের গড় x এর মাধ্যমে লেখ।

খ) প্রদত্ত শর্তানুসারে সমীকরণ গঠন করে দেখাও যে, x2 + 35x – 1950 = 0

গ) x এর মান বের করে উভয় ক্ষেত্রে নম্বরের গড় কত তা নির্ণয় কর।

সমাধান:

ক) x জন ছাত্রের প্রাপ্ত নম্বরের গড় = 1950/x

নতুন ছাত্রের নম্বরসহ (x + 1) জন ছাত্রের প্রাপ্ত নম্বরের গড় (1950 +34)/(x+1) =  1984/(x+1)

খ) প্রশ্নমতে, 1950/x = 1984/(x+1) +1

বা, 1950/x – 1984/(x+1) =1 [পক্ষান্তর করে]

বা, (1950 + 1950-1984x)/ x(x + 1) = 1

বা, x2 + x = 1950 1984 + 1950 [আড়গুণন করে]

বা, x2 + x = 1950 – 34x

.:. x + 35x – 1950 = 0 [ দেখানো হলো]

গ) x²+35x-1950 = 0

বা, x²+65x-30x – 1950 = 0

বা, x(x+65) – 30(+65) = 0

বা, (x + 65 ) (x – 30 ) = 0

x+65 = 0 অথবা  x – 30 = 0

x+65 = 0 হলে, x = -65

আবার, x – 30 = 0 হলে, x = 30

যেহেতু ছাত্রের সংখ্যা x ঋণাত্মক হতে পারে না,

সুতরাং, x ≠ −65

x =30

প্রথম ক্ষেত্রে গড় 1950/30 = 65 এবং দ্বিতীয় ক্ষেত্রে গড় 1984/31 = 64

 

দ্বিঘাত সমীকরণের মূল নির্ণয় :