লেখচিত্রের সাহায্যে দ্বিঘাত সমীকরণের সমাধান

আজকে আমরা  লেখচিত্রের সাহায্যে দ্বিঘাত সমীকরণের সমাধান সম্পর্কে  আলোচনা করবো । যা উচ্চতর গণিতের সমীকরণ অংশের অন্তর্গত।

 

 

লেখচিত্রের সাহায্যে দ্বিঘাত সমীকরণের সমাধান

দ্বিঘাত সমীকরণ ax2 + b + c = 0 এর সমাধান আমরা ইতোপূর্বে বীজগণিতীয় পদ্ধতিতে শিখেছি। এখন লেখচিত্রের সাহায্যে ইহার সমাধান পদ্ধতি আলোচনা করা হবে।

মনে করি y = ax2 + bc + c। তাহলে x এর যে সকল মানের জন্য y = 0 হবে অর্থাৎ লেখচিত্রটি -অক্ষকে ছেদ করবে, এর ঐ সকল মান-ই ax2 + bc + c = 0 সমীকরণটির সমাধান।

উদাহরণ ৩৩.

লেখচিত্রের সাহায্যে x2 – 5x +4 = 0 এর সমাধান কর।

সমাধান:

প্রদত্ত সমীকরণ  x2 – 5x +4 = 0 ………..(1) মনে করি, y = x2 – 5x +4 …….(2)

x এর কয়েকটি মানের জন্য y এর মান নির্ণয় করে (2) নং এর কয়েকটি বিন্দুর স্থানাঙ্ক নির্ণয় করি:

 

x	0	1	2	2.5	3	4	5
y	4	0	-2	-2.25	-2	0	4

 

উপরের সারণিতে প্রদত্ত বিন্দুগুলো ছক কাগজে স্থাপন করে (2) নং এর লেখচিত্র অঙ্কন করি।

 

 

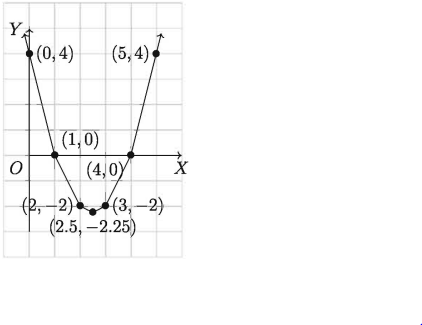
দেখা যায় যে লেখচিত্রটি X অক্ষকে (10) ও (4,0) বিন্দুতে ছেদ করেছে।

সুতরাং, (1) নং এর সমাধান x = 1, x = 4।

উদাহরণ ৩৪.

লেখচিত্রের সাহায্যে x2 – 4x+4=0 এর সমাধান কর।

প্রদত্ত সমীকরণ  x2 – 4x +4 = 0 ………..(1) মনে করি, y = x2 – 4x +4 …….(2)

x এর কয়েকটি মানের জন্য y এর মান নির্ণয় করে (2) নং এর কয়েকটি বিন্দুর স্থানাঙ্ক নির্ণয় করি:

 

x	0	1	1.5	2	2.5	3	4
y	4	1	0.25	0	0.25	1	4

 

 

উপরের সারণি হতে প্রাপ্ত বিন্দুগুলো ছক কাগজে স্থাপন করে (2) নং এর লেখচিত্র অঙ্কন করি।

 

 

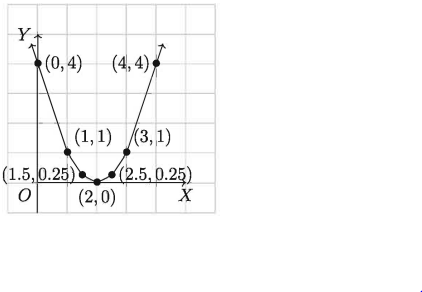
লেখচিত্রে দেখা যায় যে ইহা X অক্ষকে ( 2,0) বিন্দুতে স্পর্শ করেছে। যেহেতু দ্বিঘাত সমীকরণের দুইটি মূল থাকে, সেহেতু (1) নং এর সমাধান হবে x = 2, x = 2

উদাহরণ ৩৫.

লেখচিত্রের সাহায্যে – 2x – 1 = 0 এর সমাধান কর।

সমাধান:

প্রদত্ত সমীকরণ x2 – 2x – 10… (1) মনে করি, y = x2 – 2x – 1 … ( 2 )

সমীকরণটির লেখচিত্র অঙ্কনের জন্য x এর কয়েকটি মান নিয়ে তাদের অনুরূপ y এর মান নির্ণয় করি:

 

x	-1	-0.5	0	0.5	1	1.5	2	2.5	3
y	2	0.25	-1	-1.75	-2	-1.75	-1	0.25	2

 

 

সারণিতে স্থাপিত বিন্দুগুলো ছক কাগজে স্থাপন করে (2) নং এর লেখচিত্র অঙ্কন করি।

 

 

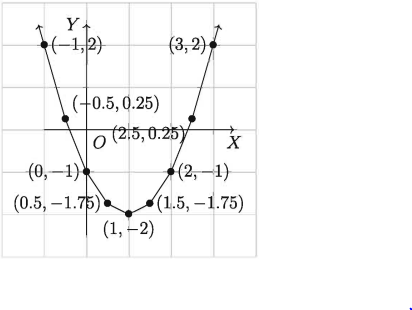
দেখা যায় যে লেখচিত্রটি X অক্ষকে ( – 0.4, 0 ) ও ( 2.4,0) বিন্দুতে ছেদ করেছে। সুতরাং, (1) নং এর সমাধান x = −0.4 (আসন্ন), x = 2.4 (আসন্ন)।

উদাহরণ ৩৬.

-12 + 3x – 2 = 0 এর মূলদ্বয় লেখচিত্রের সাহায্যে নির্ণয় কর।

সমাধান:

প্রদত্ত সমীকরণ –−x2 + 3x – 2 = 0 (1) মনে করি, y = – x2 + 3x – 2… (2)

x এর কয়েকটি মানের জন্য y এর মান নির্ণয় করে (2) নং এর লেখচিত্রের কয়েকটি বিন্দুর স্থানাঙ্ক নির্ণয় করি :

 

x	0	0.5	1	1.5	2	2.5	3
y	-2	-0.75	0	0.25	0	-0.75	-2

 

 

প্রাপ্ত বিন্দুগুলো ছক কাগজে স্থাপন করে (2) নং এর লেখচিত্র অঙ্কন করি। দেখা যায় যে লেখচিত্রটি X অক্ষের উপর (1, 0) ও (2,0) বিন্দু দিয়ে গিয়েছে। সুতরাং (1) নং এর সমাধান x = 1, x = 2

 

 

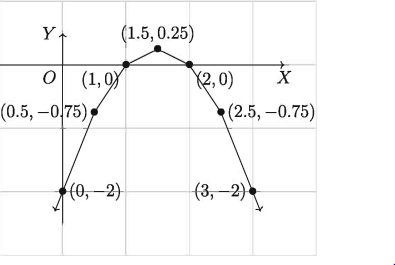
উদাহরণ ৩৭.

x2 +4x = m

ক) m = – 4 হলে, x এর মান নির্ণয় কর।

খ) 1 = 5 হলে, প্রাপ্ত সমীকরণটির নিশ্চায়ক নির্ণয় কর এবং মূলের প্রকৃতি ব্যাখ্যা কর।

গ) √m-4+√m – 10: = 6 হলে, x এর মান নির্ণয় কর।

সমাধান:

ক) দেওয়া আছে, x2 + 4x = m

এখন, m = 4 হলে, a2 + 4x = −4

বা, x2 + 4x+4 = 0

বা, (x + 2)2 = 0

বা, x + 2 = 0, x + 2 = 0

খ) দেওয়া আছে, x2 + 4x = m

এখন, m = 5 হলে, x 2 + 4x = 5

বা, x2 + 4x – 5 = 0

সমীকরণটির নিশ্চায়ক, 42 – 4.1 ( 5 ) = 16 + 20 = 36, যা একটি পূর্ণবর্গ সংখ্যা। যেহেতু সমীকরণটির নিশ্চায়ক ধনাত্মক এবং পূর্ণবর্গ সংখ্যা, সমীকরণটির মূলদ্বয় বাস্তব অসমান ও মূলদ হবে।

 

গ) দেওয়া আছে, √(m – 4)+√(m -10) =6

বা, √(m – 4) = 6 – √(m -10)

বা, √(m – 4)2 = {6 – √(m -10)}2

বা, m – 4 = 62 – 2.6.√(m -10) + m -10

বা, 12/√(m -10) = 26 + 4

বা, 12√(m -10) = 30

বা, 2√(m -10) = 5

বা, ( 2√(m -10) 2 = 25

বা, 4 (m – 10 ) = 25

বা, 4m – 40 – 25 = 0

বা, 4 ( x 2 + 4x ) – 65 = 0

বা, 4×2 + 16x – 65 =0

বা, 4x²+26x- 10x-65 = 0

বা, 2x(2x+13)-5(2x+13) = 0

বা, (2x+13) (2x-5)=0

বা, 2x+13 = 0, 2x-5=0

বা, 2x = − 13 বা, 2x = 5

বা, x = − 13/2 বা, x = 5/2 হলে সমীকরণটি সিদ্ধ হয়।

x = − 13/2 , 5/2