আজকে আমরা দ্বিপদী এর বিস্তৃতি সম্পর্কে আলোচনা করবো । যা উচ্চতর গণিতের দ্বিপদী বিস্তৃতি অংশের অন্তর্গত।

দ্বিপদী এর বিস্তৃতি
দুইটি পদের সমন্বয়ে গঠিত বীজগণিতীয় রাশিকে দ্বিপদী রাশি (Binomials) বলা হয়। a + b, x – y, 1 + x, 1 – x2, a2 – b2 ইত্যাদি দ্বিপদী রাশি। আমরা প্রথমেই একটি দ্বিপদী রাশি (1 + y) – চিহ্নিত করি। এখন (1 + y) কে যদি ক্রমাগত (1 + y) দ্বারা গুণ করতে থাকি তাহলে আমরা পাব (1+ y)², (1+ y)³, (1+y)4, (1+y)5, ইত্যাদি।
আমরা জানি,
(1 + y)2 = (1 + y) (1 + y) = 1+ 2y + y2
(1+ y)3 = (1 + y)(1 + y)² = (1 + y)(1 + 2y + y²) = 1 + 3y + 3y²+ y³
অনুরূপভাবে দীর্ঘ গুণন প্রক্রিয়ার মাধ্যমে (1 + y)4, (1 + y)5,… ইত্যাদি গুণফল নির্ণয় সম্ভব। কিন্তু (1+y) এর ঘাত বা শক্তি যত বাড়তে থাকবে গুণফল তত দীর্ঘ ও সময়সাপেক্ষ হবে। তাই এমন একটি সহজ পদ্ধতি বের করতে হবে যাতে (1 + y) এর যেকোনো ঘাত (ধরি n) বা শক্তির জন্য (1 + y)n এর বিস্তৃতি সহজেই নির্ণয় করা সম্ভব হবে। n এর মান 0, 1, 2, 3, 4,. অর্থাৎ অঋণাত্মক মানের জন্য এই অংশে আলোচনা সীমাবদ্ধ থাকবে। এখন প্রক্রিয়াটি আমরা ভালভাবে লক্ষ করি ।

উপরের বিস্তৃতিসমূহকে ভিত্তি করে আমরা (1 + y)n এর বিস্তৃতি সম্পর্কে নিম্নোক্ত সিদ্ধান্তে আসতে পারি।
ক) (1 + y)n এর বিস্তৃতিতে (n + 1) সংখ্যক পদ আছে। অর্থাৎ ঘাত বা শক্তির চেয়ে পদসংখ্যা একটি বেশি।
খ) y এর ঘাত শূন্য থেকে শুরু হয়ে 1, 2, 3, …,n পর্যন্ত বৃদ্ধি পাবে। অর্থাৎ এর ঘাত ক্রমান্বয়ে বৃদ্ধি পেয়ে n পর্যন্ত পৌঁছাবে।
দ্বিপদী সহগ
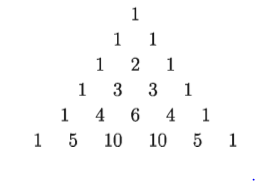
উপরের প্রত্যেক দ্বিপদী বিস্তৃতিতে y এর বিভিন্ন ঘাতের সহগকে দ্বিপদী সহগ (coefficient) বলা হয় । 1 কে y এর সহগ বিবেচনা করতে হবে। উপরের বিস্তৃতির সহগগুলোকে সাজালে আমরা পাই,
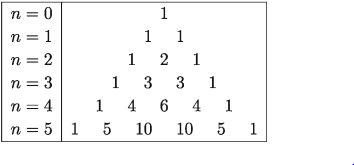
লক্ষ করলে দেখব সহগগুলো একটি ত্রিভুজের আকার ধারণ করেছে। দ্বিপদী বিস্তৃতির সহগ নির্ণয়ের এই কৌশল Blaise Pascal প্রথম ব্যবহার করেন। তাই এই ত্রিভুজকে প্যাসকেলের ত্রিভুজ (Pascal’s triangle) বলা হয়। প্যাসকেলের ত্রিভুজের সাহায্যে আমরা সহজেই দ্বিপদী রাশির বিস্তৃতিতে সহগসমূহ নির্ণয় করতে পারি।
প্যাসকেলের ত্রিভুজের ব্যবহার
প্যাসকেলের ত্রিভুজ থেকে আমরা দেখতে পাই এর বাম ও ডান দিকে 1 আছে। ত্রিভুজের মাঝখানের সংখ্যাগুলোর প্রত্যেকটি ঠিক উপরের দুইটি সংখ্যার যোগফল। নিম্নের উদাহরণটি লক্ষ করলে বিষয়টি খুব সহজেই বুঝা যাবে।
n = 5 ও n = 6 এর জন্য দ্বিপদী সহগগুলো হবে নিম্নরূপ:
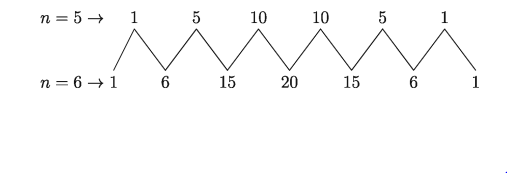
(1+y)^5 =1+5y + 10y² + 10y³ +5y4+y5
(1+y)^6=1+6y+15y²+20y³ + 15y4+6y5+y6
(1+y)^7=1+ 7y+ 21y² + 35y³ +35y4 +21y5+ 7y6+y7
আমরা যদি ভালভাবে খেয়াল করি তাহলে বুঝতে পারব এই পদ্ধতির একটি বিশেষ দুর্বলতা আছে। যেমন আমরা যদি (1 + y)’ এর বিস্তৃতি জানতে চাই তাহলে (1 + y) এর বিস্তৃতি জানা দরকার । আবার যেকোনো দ্বিপদী সহগ জানার জন্য তার ঠিক উপরের পূর্ববর্তী দুইটি সহগ জানা প্রয়োজন। এই অবস্থা থেকে উত্তরণের জন্য আমরা সরাসরি দ্বিপদী সহগ নির্ণয়ের কৌশল বের করতে চাই।
প্যাসকেলের ত্রিভুজ থেকে আমরা দেখতে পাই দ্বিপদী বিস্তৃতির সহগগুলো ঘাত n এবং পদটি কোন অবস্থানে আছে তার উপর নির্ভরশীল। আমরা একটি নতুন সাংকেতিক চিহ্ন(n r) বিবেচনা করি যেখানে n ঘাত এবং r পদের অবস্থানের সাথে সম্পর্কিত। উদাহরণস্বরূপ যদি n = 4 হয় তবে পদসংখ্যা হবে 5 টি। আমরা | পদগুলি নিম্নোক্ত উপায়ে লিখি ।
যখন n = – 4, পদসংখ্যা 5 টি: T1, T2, T3, T4, T5
তাদের সহগগুলি হলো: 1, 4, 6, 4, 1
নতুন চিহ্ন ব্যবহার করে সহগ:
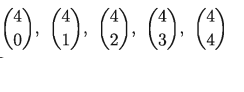
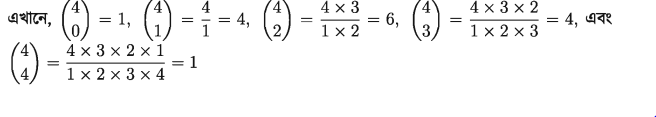
[প্যাসকেলের ত্রিভুজ থেকে সহজেই বুঝতে পারবে]
উল্লিখিত নতুন চিহ্নের সাহায্যে (n= 1, 2, 3, …) প্যাসকেলের ত্রিভুজ হবে নিচের টেবিলের অনুরূপ:
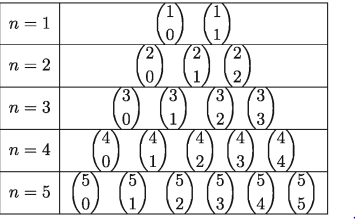
সুতরাং উপরের ত্রিভুজ থেকে আমরা খুব সহজেই বলতে পারি (1 + y)4 এর বিস্তৃতির তৃতীয় (T2+1) পদের সহগ (4 2) এবং (1 + y)5 এর বিস্তৃতির তৃতীয় (T2+1) ও চতুর্থ (T3+1) পদের সহগ যথাক্রমে (5 2)এবং (5 3)। সাধারণভাবে (1 + y)n এর বিস্তৃতির (r + 1) তম পদ (Tr+1) এর সহগ (n r)
এখন, (n r) এর মান কত তা জানার জন্য আবারো প্যাসকেলের ত্রিভুজ লক্ষ করি। প্যাসকেলের ত্রিভুজের দুইটি হেলানো পার্শ্ব থেকে আমরা দেখতে পাই,


উদাহরণ ১.
(1 + 3)5 কে বিস্তৃত কর।
সমাধান:
প্যাসকেলের ত্রিভুজের সাহায্যে –
(1 + 3x)5 = 1+5(3x) + 10(3x)² + 10(3x)³ +5(3x)4 +1(3x)5
= 1 + 15x + 90x² +270x³ +405x + 243×5
উদাহরণ ২.
(1 – 3x) কে বিস্তৃত কর।
সমাধান:
প্যাসকেলের ত্রিভুজের সাহায্যে –

(1 – 3x)5 = 1+5(-3x) + 10(-3x)² + 10(-3x)³ +5(-3x)4 +1(-3x)5
= 1 – 15x + 90x² -270x³ +405x – 243×5

মন্তব্য:
(1 + 3x) এবং ( 1 – 3x ) 5 এর বিস্তৃতি থেকে দেখা যাচ্ছে যে, উভয় বিস্তৃতি একই। শুধুমাত্র সহগের চিহ্ন পরিবর্তন করে, অর্থাৎ +, -, +,··· এর মাধ্যমে একটি থেকে অন্যটি পাওয়া সম্ভব।
উদাহরণ ৩.
(1 + 2/x)8 কে পঞ্চম পদ পর্যন্ত বিস্তৃত কর।

সমাধান:
উদাহরণ ৪.
(1 – x2/4)8 এর বিস্তৃতির x3 ও x6 এর সহগ নির্ণয় কর।
সমাধান:

(1 – x2/4)8 এর বিস্তৃতিতে দেখা যাচ্ছে এক্স৩ বর্তমান নাই। অর্থাৎ x3 এর সহগ 0 এবং x6 এর সহগ -7/8
x3 এর সহগ 0 এবং x6 এর সহগ -7/8

অনুশীলনী
১. প্যাসকেলের ত্রিভুজ বা দ্বিপদী বিস্তৃতি ব্যবহার করে (1 + y)5 এর বিস্তৃতি নির্ণয় কর। উক্ত বিস্তৃতির সাহায্যে
ক) (1 – y)5 এবং খ) (1 + 2x)5 এর বিস্তৃতি নির্ণয় কর।
২. x এর ঘাতের ঊর্ধ্বক্রম অনুসারে ক) (1 + 4x)6 এবং খ) (1 – 3x)7 এর প্রথম চার পদ পর্যন্ত বিস্তৃত কর।
৩. (1+x2)8 এর বিস্তৃতির প্রথম চারটি পদ নির্ণয় কর। উক্ত ফলাফল ব্যবহার করে (1.01)8 এর মান নির্ণয় কর।
8. x এর ঊর্ধ্বক্রম অনুসারে নিম্নোক্ত দ্বিপদীসমূহের প্রথম তিনটি পদ নির্ণয় কর।
ক) ( 1 – 2x)5
খ) (1 + 3x ) 9
৫. নিম্নোক্ত বিস্তৃতিসমূহের প্রথম চারটি পদ নির্ণয় কর। [দ্বিপদী বিস্তৃতি বা প্যাসক্যাল ত্রিভুজ এর যেকোনো একটি ব্যবহার করে]
ক) ( 1 – 2×2)7
খ) (1 + 2/x ) 4
গ) ( 1 – 1/2x)7
৬. x3 পর্যন্ত ক) (1 – x)6 এবং খ) (1 + 2x)6 বিস্তৃত কর।
