দ্বিপদী বিস্তৃতির অনুশীলনী

আজকে আমরা দ্বিপদী বিস্তৃতির অনুশীলনী সম্পর্কে  আলোচনা করবো  । যা উচ্চতর গণিতের  দ্বিপদী বিস্তৃতি অংশের অন্তর্গত।

 

 

দ্বিপদী বিস্তৃতির অনুশীলনী

১. (1+ 2x + x2)³ এর বিস্তৃতিতে-

(i) পদসংখ্যা 4

(ii) ২য় পদ 6x

(iii) শেষ পদ x6

নিচের কোনটি সঠিক?

ক) i, ii

খ) i, iii

গ) ii ও iii

ঘ) i, ii ও iii

(x+1/x)n, যেখানে n জোড় সংখ্যা। এই তথ্য থেকে ২ ও ৩ নং প্রশ্নের উত্তর দাও।

২. (r + 1) তম পদটি x বর্জিত হলে r এর মান কত?

ক) 0

খ) n/2

গ) n

ঘ) 2n

 

 

৩. n = 4 হলে, চতুর্থ পদ কত?

ক) 4

খ) 4x

গ) 4/x

ঘ) 4/x²

8. (x + y)5 -এর বিস্তৃতিতে দ্বিপদী সহগগুলি হল :

ক) 5, 10, 10, 5

খ) 1,5, 10, 10, 5, 1

গ) 10, 5, 5, 10

ঘ) 1, 2, 3, 3, 2, 1

৫. (1-x) (1+x/2)8 -এর বিস্তৃতিতে x এর সহগ .

ক) – 1

খ) 1/2

গ) 3

ঘ) – 1/2

 

 

৬. (x²+ 1 /x² ) 4 এর বিস্তৃতিতে x মুক্ত পদ কত?

ক) 4

খ) 6

গ) 8

ঘ) 0

৭. (x + y)4 বিস্তৃতির সহগগুলি সাজালে আমরা পাই-

 

 

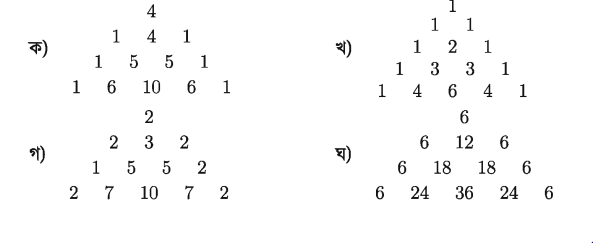
৮. নিম্নোক্ত প্রতিটি ক্ষেত্রে বিস্তৃত কর:

ক) (2+x2)5

খ) (2 -1/2x)6

৯. নিম্নোক্ত বিস্তৃতিসমূহের প্রথম চারটি পদ নির্ণয় কর।

ক) ( 2 + 3x ) 6

খ) (4 -1/2x)5

১০. (p -1/2x)6 = r- 96x + sx2 + … হলে, p, r এবং s এর মান নির্ণয় কর।

১১. (1 + x/2) 8 এর বিস্তৃতির x³ এর সহগ নির্ণয় কর।

১২. x এর ঘাতের ঊর্ধ্বক্রম অনুসারে (2+x/4)6 কে x³ পর্যন্ত বিস্তৃত কর। উহার সাহায্যে (1.9975)6 এর আসন্ন মান চার দশমিক স্থান পর্যন্ত নির্ণয় কর।

১৩. দ্বিপদী উপপাদ্য ব্যবহার করে (1.99)5 এর মান চার দশমিক স্থান পর্যন্ত নির্ণয় কর।

১৪. (1 + x/4)n এর বিস্তৃতির তৃতীয় পদের সহগ চতুর্থ পদের সহগের দ্বিগুণ। n এর মান নিৰ্ণয় কর। বিস্তৃতির পদসংখ্যা ও মধ্যপদ নির্ণয় কর।

 

 

১৫. ক) (2k – x/2)5 এর বিস্তৃতিতে k³ এর সহগ 720 হলে x এর মান নির্ণয় কর।

খ) (x² + k/x)6 এর বিস্তৃতিতে x³ এর সহগ 160 হলে k এর মান নির্ণয় কর।

১৬. A = (1 + x)7 এবং B = (1 − x) 8

ক) প্যাসকেলের ত্রিভুজ ব্যবহার করে A এর বিস্তৃতি নির্ণয় কর।

খ) B এর বিস্তৃতির চার পদ পর্যন্ত নির্ণয় করে উক্ত ফলাফল ব্যবহার করে (0.99)8 এর মান চার দশমিক স্থান পর্যন্ত নির্ণয় কর।

গ) AB এর বিস্তৃতির x7 এর সহগ নির্ণয় কর।

১৭. (A + Bx)n একটি বীজগাণিতিক রাশি ।

ক) A = 1, B = 2 এবং n = 5 হলে প্যাসকেলের ত্রিভুজ ব্যবহার করে রাশিটির বিস্তৃতি নির্ণয় কর।

খ) B = 3 এবং n = 7 হলে রাশিটির বিস্তৃতির x4 এর সহগ 22680 হয়। A এর মান নির্ণয় কর।

গ) A = 2 এবং B = 1 হলে রাশিটির বিস্তৃতির পঞ্চম ও ষষ্ঠ পদের সহগ সমান হয়। n এর মান নির্ণয় কর।

১৮. a1, a2, a3 a4 যদি (1+x)n এর বিস্তৃতির চারটি ক্রমিক পদের সহগ হয়ে থাকে তাহলে

প্রমাণ কর যে a1/( a1 + a2) + a3/( a3+ a4) = 2a2/(a2 + a3)

১৯. কোনটি বড় 99^50 + 100^50 না 101^50?

 

 

আরও দেখুনঃ

• মূলদ ও অমূলদ সূচক