আজকে আমাদের আলোচনার বিষয়ঃ পরিমিতি ঘনবস্তু। এটি নবম – দশম শ্রেনী গণিতের পরিমিতি অংশের অন্তর্গত।

পরিমিতি ঘনবস্তু
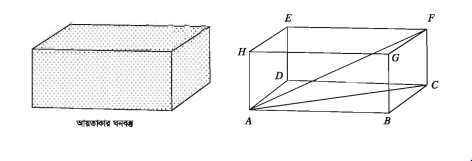
আয়তাকার ঘনবস্তু (Rectangular solid )
তিন জোড়া সমান্তরাল আয়তাকার সমতল বা পৃষ্ঠ দ্বারা আবদ্ধ ঘনবস্তুকে আয়তাকার ঘনবস্তু বলে।
মনে করি, ABCDEFGH একটি আয়তাকার ঘনবস্তু। এর দৈর্ঘ্য AB = a, প্রস্থ BC = b, উচ্চতা AH = c
১. কর্ণ নির্ণয়:
ABCDEFGH আয়তাকার ঘনবস্তুর কর্ণ AF।
∆ABC এ BC ⊥ AB এবং AC অতিভুজ।
AC2 = AB2 + BC2 = a2 + b2
আবার, ∆ABC এ FC ⊥ AC এবং AF অতিভুজ।
AF2 = AC2 + CF2 = a2 + b2 + 2
AF = √(a2 + b2 + c2)
:. আয়তাকার ঘনবস্তুরটির কর্ণ = √(a2 + b2 + c2)
২. সমগ্র তলের ক্ষেত্রফল নির্ণয়:
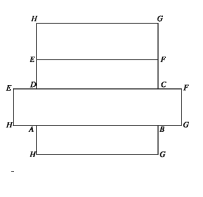
আয়তাকার ঘনবস্তুটির 6 টি তল যেখানে, বিপরীত তলগুলো পরস্পর সমান।
আয়তাকার ঘনবস্তুটির সমগ্র তলের ক্ষেত্রফল
= 2 ( ABCD তলের ক্ষেত্রফল + ABGH তলের ক্ষেত্রফল + BCFG তলের ক্ষেত্রফল)
= 2(AB × AD + AB × AH + BC × BG) = 2 (ab + ac + bc) = 2 (ab + bc + ca)
৩. আয়তাকার ঘনবস্তুর আয়তন
আয়তাকার ঘনবস্তুর আয়তন = দৈর্ঘ্য x প্রস্থ x উচ্চতা = abc
উদাহরণ ২৮.
একটি আয়তাকার ঘনবস্তুর দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে, 25 সে.মি., 20 সে.মি. এবং 15 সে.মি.। এর সমগ্র তলের ক্ষেত্রফল, আয়তন এবং কর্ণের দৈর্ঘ্য নির্ণয় কর।
সমাধান:
মনে করি, আয়তাকার ঘনবস্তুর দৈর্ঘ্য a = 25 সে.মি., প্রস্থ b 20 সে.মি. এবং উচ্চতা = c = 15 সে.মি.।
.:. আয়তাকার ঘনবস্তুটির সমগ্র তলের ক্ষেত্রফল = 2 (ab + bc + ca)
= 2 (25 × 20 + 20 x 15 + 15 x 25 ) = 2350 বর্গ সে.মি.
এবং আয়তন abc = 25 x 20 × 15 = 7500 ঘন সে.মি.
এবং কর্ণের দৈর্ঘ্য = √(a2 + b2 + c2)
= √ (252 + 202 + 152) =√ (624 + 400 + 225) = √ 1250 = 35.363 সে.মি. (প্রায়)
নির্ণেয় সমগ্র তলের ক্ষেত্রফল 2350 বর্গ সে.মি., আয়তন 7500 ঘন সে.মি. এবং কর্ণের দৈর্ঘ্য 35.363 সে.মি. (প্রায়)।
ঘনক (Cube)
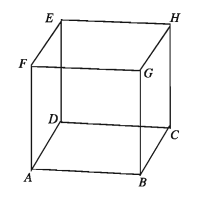
আয়তাকার ঘনবস্তুর দৈর্ঘ্য, প্রস্থ ও উচ্চতা সমান হলে একে ঘনক বলা হয়।
মনে করি, ABCDEFGH একটি ঘনক। এর দৈর্ঘ্য = প্রস্থ = উচ্চতা = ৫ একক
১. ঘনকটির কর্ণের দৈর্ঘ্য = √(a² + a² + a²) = √(3a)2 = √3a
২. ঘনকের সমগ্র তলের ক্ষেত্রফল
= 2(a.a+a.a+a.a) = 2 (a2 + a2 + a2) = 6a2
৩. ঘনকটির আয়তন = a.a.a = a3
উদাহরণ ২৯.
একটি ঘনকের সম্পূর্ণ পৃষ্ঠের ক্ষেত্রফল 96 বর্গমিটার। এর কর্ণের দৈর্ঘ্য নির্ণয় কর।
সমাধান:
মনে করি, ঘনকটির ধার a
এর সম্পূর্ণ পৃষ্ঠের ক্ষেত্রফল = 6a2 এবং কর্ণের দৈর্ঘ্য = √3a
প্রশ্নানুসারে, 6a2 = 96 বা, a2 = 16 a = 4
ঘনকটির কর্ণের দৈর্ঘ্য = √3. 4 = 6.928 মিটার (প্রায়)।
নির্ণেয় কর্ণের দৈর্ঘ্য 6.928 মিটার (প্রায়)।
বেলন (Cylinder)
কোনো আয়তক্ষেত্রের যে কোনো বাহুকে অক্ষ ধরে আয়তক্ষেত্রটিকে ঐ বাহুর চতুর্দিকে ঘোরালে যে ঘনবস্তুর সৃষ্টি হয়, তাকে সমবৃত্তভূমিক বেলন বা সিলিন্ডার বলা হয়। সমবৃত্তভূমিক বেলনের দুই প্রান্তকে বৃত্তাকার তল, বক্রতলকে বক্রপৃষ্ঠ এবং সমগ্রতলকে পৃষ্ঠতল বলা হয়। আয়তক্ষেত্রের অক্ষের সমান্তরাল ঘূর্ণায়মান বাহুটিকে বেলনের সৃজক বা উৎপাদক রেখা বলে।
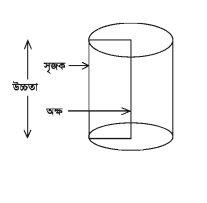
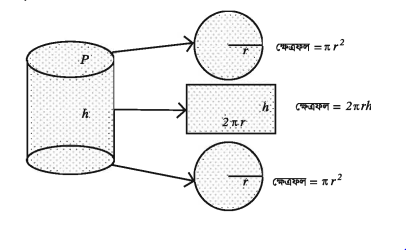
উপরের, চিত্রটি একটি সমবৃত্তভূমিক বেলন যার ভূমির ব্যাসার্ধ r এবং উচ্চতা h
১. ভূমির ক্ষেত্রফল = πr2
২. বক্রপৃষ্ঠের ক্ষেত্রফল = ভূমির পরিধি × উচ্চতা= 2πrh
৩. সম্পূর্ণ তলের ক্ষেত্রফল বা সমগ্র তলের ক্ষেত্রফল
বা, পৃষ্ঠতলের ক্ষেত্রফল = (πr2 + 2πrh + πr2) = 2πr (r + h)
৪. আয়তন = ভূমির ক্ষেত্রফল x উচ্চতা= πr2h
উদাহরণ ৩০.
একটি সমবৃত্তভূমিক বেলনের উচ্চতা 10 সে.মি. এবং ভূমির ব্যাসার্ধ 7 সে.মি. হলে, এর আয়তন এবং সম্পূর্ণ পৃষ্ঠের ক্ষেত্রফল নির্ণয় কর।
সমাধান:
মনে করি, সমবৃত্তভূমিক বেলনের উচ্চতা h = 10 সে.মি. এবং ভূমির ব্যাসার্ধ r
এর আয়তন = πr²h
= 3.1416 x 72 × 10 = 1539.38 ঘন সে.মি. (প্রায়)
এবং সমগ্র পৃষ্ঠের ক্ষেত্রফল 2πr(r+h)
= 2 × 3.1416 x 7 (7 +10) = 747.7 বর্গমিটার (প্রায়)
উদাহরণ ৩১.
ঢাকনাসহ একটি বাক্সের বাইরের মাপ যথাক্রমে 10 সে.মি., 9 সে.মি. ও 7 সে.মি.। বাক্সটির ভিতরের সমগ্র পৃষ্ঠের ক্ষেত্রফল 262 বর্গ সে. মি. এবং বাক্সের পুরুত্ব সমান।
ক) বাক্সটির আয়তন নির্ণয় কর।
খ) বাক্সটির দেওয়ালের পুরুত্ব নির্ণয় কর।
গ) বাক্সটির বৃহত্তম দৈর্ঘ্যের সমান বাহুবিশিষ্ট কোনো রম্বসের একটি কর্ণ 16 সে.মি. হলে রম্বসটির ক্ষেত্রফল নির্ণয় কর।
সমাধান :
ক) বাক্সটির বাইরের মাপ যথাক্রমে 10 সে.মি., 9 সে.মি. ও 7 সে.মি.
বাক্সটির বাইরের আয়তন = 10 x 9 x 7 = 630 ঘন সে.মি.।
খ) মনে করি, বাক্সের পুরুত্ব x ঢাকনাসহ বাক্সের বাইরের মাপ যথাক্রমে 10 সে.মি., 9 সে.মি. ও 7 সে.মি.
বাক্সের ভিতরের মাপ যথাক্রমে a = (10 – 2x) সে.মি., b = (9 – 2x) সে.মি.
এবং c = (7 – 2x) সে.মি.
বাক্সের ভিতরের সমগ্র তলের ক্ষেত্রফল = 2 (ab + bc + ca)
প্রশ্নানুসারে, 2(ab + bc + ca) = 262
বা,(10-2x)(9-2x) + (9-2x) (7 -2x) + (7 — 2x) (10 -2x) = 131
বা, 90-38x+4x² + 63 – 32x + 4×2 + 70-34x+4x² – 131 = 0
বা, 12×2 – 104x + 92 = 0
বা, 3×2 – 26x + 23 = 0
বা, 3x 2 – 3x – 23x + 23 = 0
বা, 3x (x – 1 ) – 23 ( x – 1 ) = 0
বা, (x – 1) (3x – 23 ) = 0
বা, x – 1 = 0 অথবা 3x – 23 = 0 –
বা, x = 1 অথবা, x = 23 3 = 7.67 (প্রায়)
বাক্সটির পুরুত্ব তার বাইরের তিনটি পরিমাপের কোনটির চেয়েই বড় হতে পারে না।
নির্ণেয় বাক্সের পুরুত্ব 1 সে.মি.
গ) মনে করি, ABCD রম্বসের প্রত্যেক বাহুর দৈর্ঘ্য 10 সে.মি. এবং কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করে।
আমরা জানি, রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে।
OA = OC, OB = OD
∆AOB সমকোণী ত্রিভুজে অতিভুজ AB = 10
এখানে, AB2 = 102 = 100 = 36 +64 = 62 + 82 = OB2 + OA2 [চিত্র অনুযায়ী]
OB = 6, OA = 8
কর্ণ AC = 2 x 8 = 16 সে.মি. এবং কর্ণ BD = 2 x 6 = 12 সে.মি.
ABCD রম্বসের ক্ষেত্রফল = 1/2 × AC × BD = 1/2 × 16 × 12 = 96 বর্গ সে.মি.

উদাহরণ ৩২.
কোনো ঘনকের পৃষ্ঠতলের কর্ণের দৈর্ঘ্য 8√2 সে.মি. হলে, এর কর্ণের দৈর্ঘ্য ও আয়তন নির্ণয় কর।
সমাধান:
মনে করি, ঘনকের ধার a
ঘনকটির পৃষ্ঠতলের কর্ণের দৈর্ঘ্য = √2a, কর্ণের দৈর্ঘ্য = √3a এবং আয়তন = a3
প্রশ্নানুসারে, √2a = 8√2 বা, a = 8
ঘনকটির কর্ণের দৈর্ঘ্য = √3 x 8 = 13.856 সে.মি. (প্রায়)
এবং আয়তন = 83 = 512 ঘন সে.মি.।
নির্ণেয় কর্ণের দৈর্ঘ্য 13.856 সে.মি. (প্রায়) এবং আয়তন 512 ঘন সে.মি.।

উদাহরণ ৩৩.
কোনো আয়তক্ষেত্রের দৈর্ঘ্য 12 সে.মি. এবং প্রস্থ 5 সে.মি.। একে বৃহত্তর বাহুর চতুর্দিকে ঘোরালে যে ঘনবস্তু উৎপন্ন হয় তার পৃষ্ঠতলের ক্ষেত্রফল এবং আয়তন নির্ণয় কর।
সমাধান:
দেওয়া আছে একটি আয়তক্ষেত্রের দৈর্ঘ্য 12 সে.মি. এবং প্রস্থ 5 সে.মি.। একে বৃহত্তর বাহুর চতুর্দিকে ঘোরালে একটি সমবৃত্তভূমিক বেলন আকৃতির ঘনবস্তু উৎপন্ন হবে, যার উচ্চতা h = 12 সে.মি. এবং ভূমির ব্যাসার্ধ r = 5 সে.মি.।
উৎপন্ন ঘনবস্তুর পৃষ্ঠতলের ক্ষেত্রফল = 2πr (r + h)
= 2 x 3.1416 x 5 (5+12 ) = 534.071 বর্গ সে.মি. (প্রায়)
এবং আয়তন = πr2h
= 3.1416 x 52 x 12 = 942.48 ঘন সে.মি. (প্রায়)
নির্ণেয় পৃষ্ঠতলের ক্ষেত্রফল 534.071 বর্গ সে.মি. (প্রায়) এবং আয়তন 942.48 ঘন সে.মি. (প্রায়)