আজকে আমরা জ্যামিতিতে পিথাগোরাসের উপপাদ্য সম্পর্কে আলোচনা করবো । যা উচ্চতর গণিতের জ্যামিতি অংশের অন্তর্গত।

জ্যামিতিতে পিথাগোরাসের উপপাদ্য
খ্রিষ্টের জন্মের প্রায় ৬০০ বছর আগে বিখ্যাত গ্রিক পণ্ডিত পিথাগোরাস (জন্ম খ্রিষ্টপূর্ব ৫৭০-মৃত্যু খ্রিষ্টপূর্ব ৪৯৫) সমকোণী ত্রিভুজের ক্ষেত্রে একটি অত্যন্ত গুরুত্বপূর্ণ উপপাদ্য (theorem) বর্ণনা করেন। এই উপপাদ্যটি তার নামানুসারে পিথাগোরাসের উপপাদ্য বলে পরিচিত। জানা যায় তারও প্রায় ১০০০ বছর আগে মিশরীয় ভূমি জরিপকারীগণের এই উপপাদ্যটি সম্বন্ধে ধারণা ছিল। পিথাগোরাসের উপপাদ্য বিভিন্নভাবে প্রমাণ করা যায়। নিম্ন মাধ্যমিক পর্যায়ে এর দুইটি প্রমাণ দেওয়া আছে। তাই এখানে কোনো প্রমাণ দেওয়া হবে না। এখানে শুধুমাত্র এর বর্ণনা ও কিছু আলোচনা থাকবে।
উপপাদ্য ১ (পিথাগোরাসের উপপাদ্য)
একটি সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টির সমান।
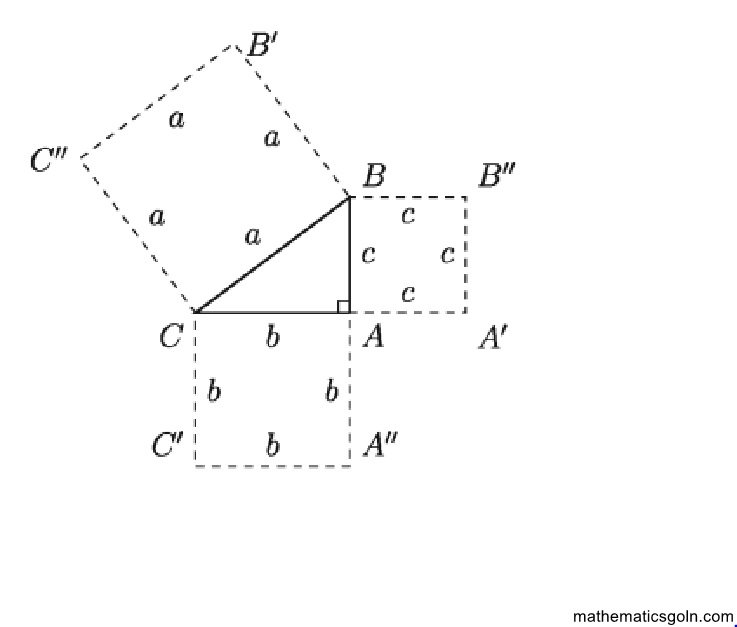
উপরের চিত্রে ABC একটি সমকোণী ত্রিভুজ। LBAC সমকোণ এবং BC অতিভুজ। BC অতিভুজের উপর কোনো বর্গক্ষেত্র অঙ্কন করলে তার যে ক্ষেত্রফল হবে সমকোণ সংলগ্ন বাহুদ্বয় AB ও AC এর উপর বর্গক্ষেত্র অঙ্কন করলে তাদের ক্ষেত্রফলের যোগফল তার সমান হবে।
এখানে BC2 BB’C”C বর্গক্ষেত্রের ক্ষেত্রফল = a2, AB2 = AA’ B” B বর্গক্ষেত্রের ক্ষেত্রফল c2 = 2, এবং CA2 = CC’A” A বর্গক্ষেত্রের ক্ষেত্রফল = b2
অতএব BC2 = AB2 = AC2
বা a2 = b2 + c2
উদাহরণস্বরূপ, একটি সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহুদ্বয়ের দৈর্ঘ্য চ = 8 সে.মি. ও c = 6 সে.মি. হলে পিথাগোরাসের উপপাদ্যের মাধ্যমে বলা যায় এর অতিভুজের দৈর্ঘ্য a = 10 সে.মি.।
অনুরূপভাবে, যেকোনো দুই বাহুর দৈর্ঘ্যের মাধ্যমে তৃতীয় বাহুর দৈর্ঘ্য জানা সম্ভব।
উপপাদ্য ২ (পিথাগোরাসের উপপাদ্যের বিপরীত উপপাদ্য)
কোনো ত্রিভুজের একটি বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টির সমান হলে শেষোক্ত বাহুদ্বয়ের অন্তর্ভুক্ত কোণটি সমকোণ হবে।
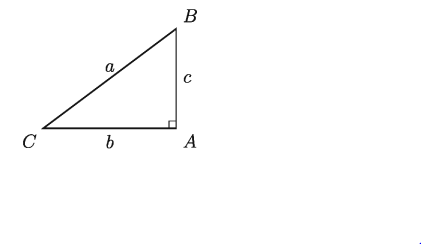
উপরের চিত্রে AABC এর তিনটি বাহু যথাক্রমে AB, BC ও AC। BC বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহু AB ও AC এর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টির সমান। অর্থাৎ, BC2 AB2 = AC2 বা, 2 b2 + 2। সুতরাং, LBAC একটি সমকোণ = = উদাহরণস্বরূপ আমরা বলতে পারি AABC এর AB, BC ও CA বাহুর দৈর্ঘ্য যথাক্রমে 6 সে.মি. 10 সে.মি. ও ৪ সে.মি. হলে LBAC অবশ্যই সমকোণ হবে।
যেহেতু, AB2 = 62 বর্গ সে.মি. = 36 বর্গ সে.মি.,
BC2 102 বর্গ সে.মি. = 100 বর্গ সে.মি.,
AC2 = 82 বর্গ সে.মি. = 64 বর্গ সে.মি.,
BC2 = 100 = 36 + 64 = AB2 = AC2
∠BAC = 90° = এক সমকোণ ।
বিন্দুর লম্ব অভিক্ষেপ (Orthogonal Projection of a Point):
কোনো নির্দিষ্ট সরলরেখার উপর কোনো বিন্দুর লম্ব অভিক্ষেপ বলতে সেই বিন্দু থেকে উক্ত নির্দিষ্ট রেখার উপর অঙ্কিত লম্বের পাদবিন্দুকে বুঝায়। মনে করি, XY একটি নির্দিষ্ট সরলরেখা এবং P যেকোনো বিন্দু (নিচের চিত্রে)। P বিন্দু থেকে XY রেখার উপর অঙ্কিত লম্ব PP’ এবং এই লম্বের পাদবিন্দু P”। সুতরাং, P’ বিন্দু XY রেখার উপর P বিন্দুর লম্ব অভিক্ষেপ। কোনো নির্দিষ্ট রেখার উপর কোনো বিন্দুর লম্ব অভিক্ষেপ একটি বিন্দু।
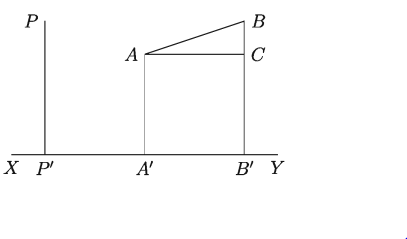
রেখাংশের লম্ব অভিক্ষেপ (Orthogonal Projection of a Line ) :
ধরি, AB রেখাংশের প্রান্ত বিন্দুদ্বয় A ও B (উপরের চিত্রে)। এখন A ও B বিন্দু থেকে XY রেখার উপর অঙ্কিত লম্ব যথাক্রমে AA’ ও BB’। AA’ লম্বের পাদবিন্দু A এবং BB’ লম্বের পাদবিন্দু B’। এই A’B’ রেখাংশই হচ্ছে XY রেখার উপর AB রেখাংশের লম্ব অভিক্ষেপ। সুতরাং, দেখা যাচ্ছে লম্ব অঙ্কনের মাধ্যমে অভিক্ষেপ নির্ণয় করা হয়। তাই A’B’ রেখাংশকে XY রেখার উপর AB রেখাংশের লম্ব অভিক্ষেপ বলা হয়। উপরের চিত্রে AB রেখাংশ XY এর সমান্তরাল হলে AB = A’B’ হবে। আমরা এ ধারণা থেকে বলতে পারি কোনো সরলরেখার উপর লম্ব যেকোনো সরলরেখার লম্ব অভিক্ষেপ একটি বিন্দু। সে ক্ষেত্রে উক্ত লম্ব অভিক্ষেপের দৈর্ঘ্য হবে শূন্য।
দ্রষ্টব্য:
১. কোনো রেখার উপর কোনো বিন্দু থেকে অঙ্কিত লম্বের পাদবিন্দুই ঐ বিন্দুর লম্ব অভিক্ষেপ।
২. কোনো রেখার উপর ঐ রেখার লম্ব রেখাংশের লম্ব অভিক্ষেপ একটি বিন্দু যার দৈর্ঘ্য শূন্য।
৩. কোন রেখার উপর ঐ রেখার সমান্তরাল কোনো রেখাংশের লম্ব অভিক্ষেপের দৈর্ঘ্য ঐ রেখাংশের দৈর্ঘ্যের সমান।
কতিপয় গুরুত্বপূর্ণ উপপাদ্য
পিথাগোরাসের উপপাদ্যের উপর ভিত্তি করে এবং লম্ব অভিক্ষেপের ধারণার সাহায্যে আমরা এখন কয়েকটি গুরুত্বপূর্ণ উপপাদ্যের যুক্তিমূলক প্রমাণ উপস্থাপন করবো।
উপপাদ্য ৩.
স্থূলকোণী ত্রিভুজের স্থূলকোণের বিপরীত বাহুর উপর অঙ্কিত বর্গক্ষেত্র ঐ কোণের সন্নিহিত অন্য দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফল এবং ঐ দুই বাহুর যেকোনো একটি ও তার উপর অপর বাহুর লম্ব অভিক্ষেপের অন্তর্গত আয়তক্ষেত্রের ক্ষেত্রফলের দ্বিগুণের সমষ্টির সমান।
বিশেষ নির্বচন:
মনে করি ABC ত্রিভুজের ZBCA স্থূলকোণ, AB স্থূলকোণের বিপরীত বাহু এবং স্থূলকোণের সন্নিহিত বাহুদ্বয় BC ও AC।
BC বাহুর বর্ধিতাংশের উপর AC বাহুর লম্ব অভিক্ষেপ CD (নিচের চিত্র)। প্রমাণ করতে হবে যে, AB2 = AC2 + BC2 + 2BC.CD
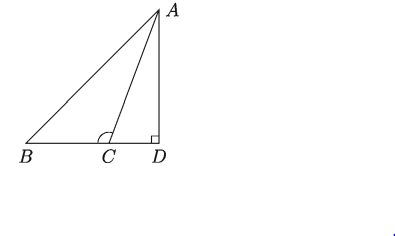
প্রমাণ:
BC বাহুর বর্ধিতাংশের উপর AC বাহুর লম্ব অভিক্ষেপ CD হওয়ায় ∆ABD একটি সমকোণী ত্রিভুজ এবং ∠ADB সমকোণ।
সুতরাং পিথাগোরাসের উপপাদ্য অনুসারে
AB2 = AD2 + BD 2
= AD2 + (BC + CD) 2 [ BD = BC + CD]
= AD2 + BC2 + CD 2 + 2BC.CD
.. AB2 = AD2 + CD2 + BC2 + 2. BC.CD …… (1)
আবার AACD সমকোণী ত্রিভুজ এবং ∠ADC সমকোণ।
AC2 = AD2 + CD 2 … ..(2)
(2) নং সমীকরণ হতে AD2 + CD2 = AC2 (1) নং সমীকরণে বসিয়ে পাই,
AB2 = AC2 + BC2 + 2BC.CD [প্রমাণিত]
উপপাদ্য ৪.
যেকোনো ত্রিভুজের সূক্ষ্মকোণের বিপরীত বাহুর উপর অঙ্কিত বর্গক্ষেত্র অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টি অপেক্ষা ঐ দুই বাহুর যেকোনো একটি ও তার উপর অপরটির লম্ব অভিক্ষেপের অন্তর্গত আয়তক্ষেত্রের ক্ষেত্রফলের দ্বিগুণ পরিমাণ কম।
বিশেষ নির্বচন:
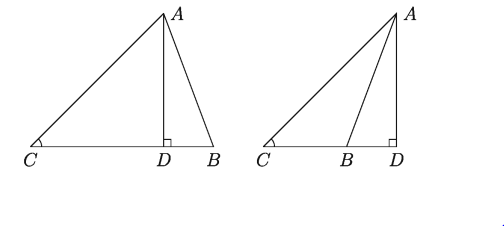
∆ABC ত্রিভুজের ∆ACB সূক্ষ্মকোণ এবং সূক্ষ্মকোণের বিপরীত বাহু AB। অপর দুই বাহু AC ও BC। মনে করি, BC বাহুর উপর (নিচের বাম পাশের চিত্র) এবং BC বাহুর বর্ধিতাংশের উপর (নিচের ডান পাশের চিত্র) লম্ব AD। তাহলে উভয় ত্রিভুজের ক্ষেত্রে BC বাহুর উপর AC বাহুর লম্ব অভিক্ষেপ CD। প্রমাণ করতে হবে যে AB2 = AC2 + BC2 – 2. BC. CD
[উল্লেখ করা দরকার যে এখানে A থেকে BC এর উপর লম্ব টানা হয়েছে। কিন্তু B বিন্দু থেকে AC এর উপর লম্ব অঙ্কনের মাধ্যমেও একইভাবে উপপাদ্যটি প্রমাণ করা যায়।]
প্রমাণ:
∆ADB সমকোণী ত্রিভুজ এবং LADB সমকোণ।
পিথাগোরাসের উপপাদ্য অনুসারে AB2 = AD2 + BD2 (1)
উপরের বামের চিত্রে BD = BC – CD
:. BD2 = (BC – CD) 2 = BC2 + CD 2 – 2. BC. CD
উপরের ডানের চিত্রে BD = CD- BC
:. BD2 = (CD – BC ) 2 = CD 2 + BC2 – 2. CD- BC
সুতরাং উভয় চিত্রে BD 2 = BC2 + CD2 – 2. BC.CD (2)
এখন সমীকরণ (1) ও (2) হতে পাওয়া যায়,
AB2 = AD2 + BC2 + CD 2 – 2. BC.CD
বা, AB2 = AD2 + CD 2 + BC2 – 2. BC. CD (3)
আবার AADC সমকোণী ত্রিভুজ এবং LADC সমকোণ।
পিথাগোরাসের উপপাদ্য অনুসারে AC2 = AD2 + CD2 (4)
সমীকরণ (3) ও (4) হতে পাওয়া যায়, AB2 = AC2 + BC2 – 2. BC. CD [প্রমাণিত]
মন্তব্য:
১. সমকোণী ত্রিভুজের ক্ষেত্রে সমকোণের সন্নিহিত বাহুদ্বয় পরস্পর লম্ব বিধায় তাদের প্রত্যেকটির উপর অপরটির লম্ব অভিক্ষেপ শূন্য। LACB সমকোণ হলে BC এর উপর AC এর লম্ব অভিক্ষেপ CD = 0। সুতরাং BC – CD = 0, ফলে AB2 = AC2 + BC2
২. উপপাদ্য ৩ ও উপপাদ্য ৪, উপপাদ্য ১ এর ভিত্তির উপর প্রতিষ্ঠিত। তাই উপপাদ্য ৩ ও উপপাদ্য ৪ কে উপপাদ্য ১ অর্থাৎ পিথাগোরাসের উপপাদ্যের অনুসিদ্ধান্ত বলা যায়।
উপরোক্ত আলোচনা সাপেক্ষে গৃহীত সিদ্ধান্তসমূহ: AABC এর ক্ষেত্রে,
∆ACB স্থূলকোণ হলে, AB2 > AC2 + BC2
[উপপাদ্য ৩]
খ) LACB সমকোণ হলে, AB2 = AC2 + BC2
[উপপাদ্য ১]
গ) LACB সূক্ষ্মকোণ হলে, AB2 < AC2 + BC2 [উপপাদ্য ৪]
নিচের উপপাদ্যটি এ্যাপোলোনিয়াস (জন্ম খৃষ্ঠপূর্ব ২৪০-মৃত্যু খৃষ্ঠপূর্ব ১৯০) কর্তৃক বর্ণিত বলে এটি এ্যাপোলোনিয়াসের উপপাদ্য নামে পরিচিত। এটি পিথাগোরাসের উপপাদ্যের বিস্তার অর্থাৎ উপপাদ্য ৩ ও উপপাদ্য ৪ এর উপর ভিত্তি করে প্রতিষ্ঠিত।
উপপাদ্য ৫ (এ্যাপোলোনিয়াসের উপপাদ্য)
ত্রিভুজের যেকোনো দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টি, তৃতীয় বাহুর অর্ধেকের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল এবং ঐ বাহুর সমদ্বিখণ্ডক মধ্যমার উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলের সমষ্টির দ্বিগুণ।
বিশেষ নির্বচন:
AABC এর AD মধ্যমা BC বাহুকে সমদ্বিখণ্ডিত করেছে। প্রমাণ করতে হবে যে, AB2 + AC2 = 2(AD 2 + BD 2 )
প্রমাণ:
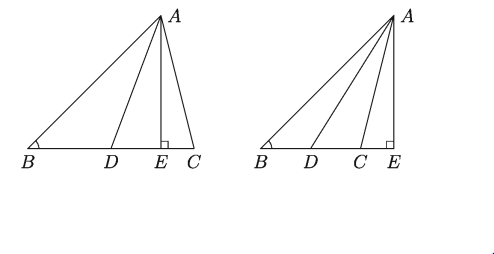
BC বাহুর উপর (উপরের বাম পাশের চিত্রে) এবং BC বাহুর বর্ধিতাংশের উপর (উপরের ডান পাশের চিত্রে) AE লম্ব অঙ্কন করি। উভয় চিত্রে AABD এর LADB স্থূলকোণ এবং BD রেখার বর্ধিতাংশের উপর AD রেখার লম্ব অভিক্ষেপ DE
স্থূলকোণের ক্ষেত্রে পিথাগোরাসের উপপাদ্যের বিস্তৃতি অনুসারে [উপপাদ্য ৩] আমরা পাই,
AB2 = AD2 + BD 2 + 2. BD. DE…(1)
এখানে, AACD এর LADC সূক্ষ্মকোণ এবং DC রেখার (উপরের বাম পাশের চিত্রে) এবং DC রেখার বর্ধিতাংশের (উপরের ডান পাশের চিত্রে) উপর AD রেখার লম্ব অভিক্ষেপ DE।
সূক্ষ্মকোণের ক্ষেত্রে পিথাগোরাসের উপপাদ্যের বিস্তৃতি অনুসারে [উপপাদ্য ৪] আমরা পাই, AC2 = AD2 + CD 2 – 2. CD.DE. · (2)
এখন সমীকরণ (1) ও (2) যোগ করে পাই,
AB2 + AC2 = 2AD2 + BD 2 + CD 2 + 2. BD. DE – 2. CD. DE : AB2 + AC2 = 2 ( AD2 + BD 2 ) [প্রমাণিত]
= 2AD2 + 2BD2 [ BD = CD ]
এ্যাপোলোনিয়াসের উপপাদ্যের মাধ্যমে ত্রিভুজের বাহু ও মধ্যমার সম্পর্ক নির্ণয়
মনে করি, AABC এর BC, CA ও AB বাহুর দৈর্ঘ্য যথাক্রমে a, b ও cl BC, CA ও AB বাহুর উপর অঙ্কিত মধ্যমা AD, BE ও CF এর দৈর্ঘ্য যথাক্রমে d e e f ।
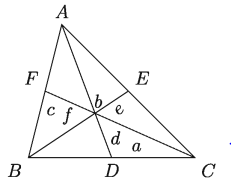
তাহলে, এ্যাপোলোনিয়াসের উপপাদ্য হতে পাই,
AB²+ AC²=2(AD² + BD²)
বা, c²+b²=2{d² + (1/2a)2)} [.: BD = 1/2a]
বা, b²+c² = 2d²+2.1/4a2
বা, b²+c² = 2d² + a²/2
বা, d2 = {2(b2+c²)-a2}/4
অনুরূপভাবে পাওয়া যায়, e2 = {2(c² + a²) – b2} /4 এবং f2 = {2(a² + b²) – c²}/ 4
সুতরাং বলা যায় কোনো ত্রিভুজের বাহুগুলোর দৈর্ঘ্য জানা থাকলে মধ্যমাসমূহের দৈর্ঘ্য জানা যায়।
আবার, d² + e² +ƒ² = 2(b²+c²) – a²/4 + 2(c² + a²) − b²/4 + 2(a² + b²) – c²/4
অর্থাৎ, d² + e² + ƒ² = = 3/4(a+b²+c²)
3(a²+b²+c²)=4(d² + e² + ƒ²)
সুতরাং বলা যায় কোন ত্রিভুজের তিনটি বাহুর উপর অঙ্কিত বর্গক্ষেত্রসমূহের ক্ষেত্রফলের সমষ্টির তিনগুণ উক্ত ত্রিভুজের মধ্যমাত্রয়ের উপর অঙ্কিত বর্গক্ষেত্রসমূহের ক্ষেত্রফলের সমষ্টির চারগুণের সমান।
ত্রিভুজটি সমকোণী অর্থাৎ LACB সমকোণ এবং AB অতিভুজ হলে
c² = a² + b²
বা, a2 + b2 + c2 = 2c²
বা, = 4/3 (d² + e2 + f2) = 2c²
বা, 2 (d² + e2 + f2) = 3c²
সুতরাং, বলা যায় সমকোণী ত্রিভুজের মধ্যমাত্রয়ের উপর অঙ্কিত বর্গক্ষেত্রসমূহের ক্ষেত্রফলের সমষ্টির দ্বিগুণ অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলের তিনগুণের সমান।
