আজকে আমাদের আলোচনার বিষয়ঃ পিথাগোরাসের উপপাদ্যের প্রমাণ। এটি অষ্টম শ্রেনী গণিতের পিথাগোরাসের উপপাদ্য এর অন্তর্গত।
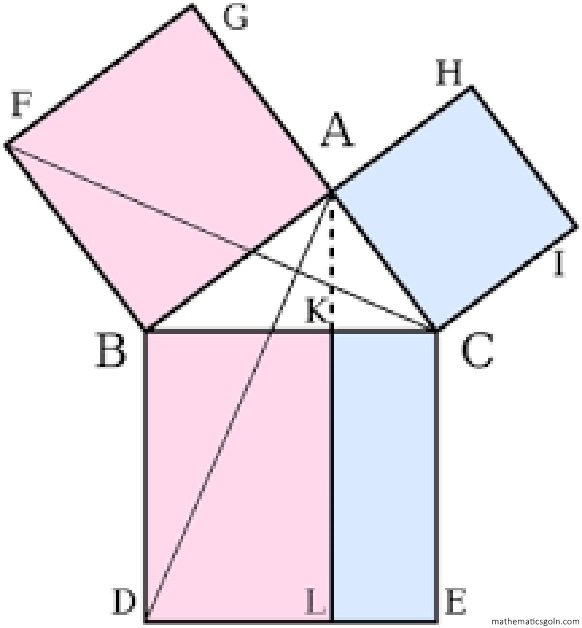
পিথাগোরাসের উপপাদ্যের প্রমাণ
একটি সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্র অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের সমষ্টির সমান ।
(দুইটি সমকোণী ত্রিভুজের সাহায্যে )
বিশেষ নির্বচন :
মনে করি, ABC সমকোণী ত্রিভুজের ∠B = 90°
অতিভুজ AC = b, AB = c ও BC = a
প্রমাণ করতে হবে যে, AC2 = AB 2 + BC2 অর্থাৎ
b² = c² + a²
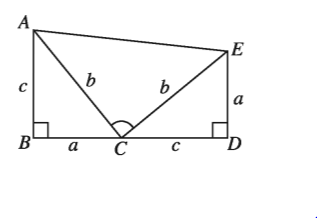
অঙ্কন :
BC কে D পর্যন্ত বর্ধিত করি, যেন CD = AB = c হয় । D বিন্দুতে বর্ধিত BC এর উপর DE লম্ব আঁকি, যেন DE = BC = a হয় । C, E ও A, E যোগ করি ।
প্রমাণ :
|
ধাপ |
যথার্থতা |
| (১) ∆ABC ও ∆CDE এ AB = CD = c, BC = DE = a এবং অন্তর্ভুক্ত ∠ABC = অন্তর্ভুক্ত ∠CDE |
সুতরাং, ∆ABC = ∆CDE AC = CE = b এবং ∠BAC = ∠ECD (২) আবার, AB ⊥ BD এবং ED ⊥ BD বলে AB || ED সুতরাং, ABDE একটি ট্রাপিজিয়াম । (৩) তদুপরি, ∠ACB + ∠BAC = ∠ACB + ∠ECD = এক সমকোণ । :. ∠ACE এক সমকোণ । ∆ACE সমকোণী ত্রিভুজ । এখন ABDE ট্রাপিজিয়ামক্ষেত্রের ক্ষেত্রফল = (∆ক্ষেত্র ABC + ∆ক্ষেত্র CDE + ∆ক্ষেত্র ACE) বা, 1/2BD(AB + DE) = 1/2ac +1/2ac +1/2b² বা, 1/2(BC+ CD) (AB + DE) = 1/2[2ac + b²] বা, (a+c)(a+c) = 2ac + b2 [ 2 দ্বারা গুণ করে ] বা, a2 + 2ac + c2 = 2ac + b2 b2 = c2 + c2 (প্রমাণিত) |
[ প্রত্যেকে সমকোণ ]
[ বাহু-কোণ-বাহু উপপাদ্য ] :: ∠BAC = ∠ECD [ ট্রাপিজিয়াম ক্ষেত্রের ক্ষেত্রফল = 1/2 সমান্তরাল বাহুদ্বয়ের যোগফল x সমান্তরাল বাহুদ্বয়ের মধ্যবর্তী দূরত্ব] |
পিথাগোরাসের উপপাদ্যের বিকল্প প্রমাণ (সদৃশকোণী ত্রিভুজের সাহায্যে)
বিশেষ নির্বচন :
মনে করি, ABC সমকোণী ত্রিভুজের ∠C = 90° এবং অতিভুজ AB = C, BC = a, AC = b
প্রমাণ করতে হবে যে, AB2 = AC2 + BC2
অর্থাৎ c2 = a2 + b2
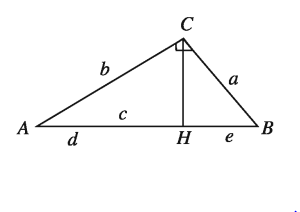
অঙ্কন :
C বিন্দু থেকে অতিভুজ AB এর উপর লম্ব CH অঙ্কন করি । AB অতিভুজ H বিন্দুতে d ও e অংশে বিভক্ত হলো ।
প্ৰমাণ :
|
ধাপ |
যথার্থতা |
| ∆BCH ও ∆ABC এ
∠BHC = ∠ACB এবং ∠CBH = ∠ABC (১) ∆CBH ও ∆ABC সদৃশ। BC/AB = BH/BC a/c = e/a ….. ….. (1) (২) অনুরূপভাবে ∆ACH ও ∆ABC সদৃশ । b/c = d / b ….. ….. (2) (৩) অনুপাত দুইটি থেকে পাই, a2 = c x e , b2 = c x d অতএব, a2 + b2 = c x e + c x d = c (e+d) = c x c = c2 c2 = a2 + b2 [ প্রমাণিত ] |
প্রত্যেকেই সমকোণ সাধারণ কোণ
[(i) উভয় ত্রিভুজ সমকোণী :: c = e+d |
পিথাগোরাসের উপপাদ্যের বিকল্প প্রমাণ
(বীজগণিতের সাহায্যে)
পিথাগোরাসের উপপাদ্য বীজগণিতের সাহায্যে সহজেই প্রমাণ করা যায় ।
বিশেষ নির্বচন :
মনে করি, একটি সমকোণী ত্রিভুজের অতিভুজ c এবং a, b যথাক্রমে অন্য দুই বাহু ।
প্রমাণ করতে হবে, c2 = a2 + b2
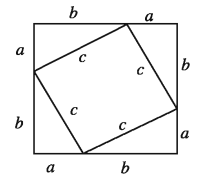
অঙ্কন :
প্রদত্ত ত্রিভুজটির সমান করে চারটি ত্রিভুজ চিত্রে প্রদর্শিত উপায়ে আঁকি ।
প্ৰমাণ :
|
ধাপ |
যথার্থতা |
| (১) অঙ্কিত বড় ক্ষেত্রটি বর্গক্ষেত্র।
এর ক্ষেত্রফল (a+b)2 (২) ছোট চতুর্ভুজ ক্ষেত্রটি বর্গক্ষেত্র । এর ক্ষেত্রফল c2 (৩) অঙ্কনানুসারে, বড় বর্গক্ষেত্রের ক্ষেত্রফল চারটি ত্রিভুজক্ষেত্র ও ছোট বর্গক্ষেত্রের ক্ষেত্রফলের সমষ্টির সমান । অর্থাৎ, (a+b)2 =4 x 1/2 x a x b + c2 বা, a2 + 2ab + b2 = 2ab + c2 c2 = a2 + b2 (প্রমাণিত ) |
[বাহুগুলোর প্রত্যেকটির দৈর্ঘ্য a+b এবং কোণগুলো সমকোণ ]
[বাহুগুলোর প্রত্যেকটির দৈর্ঘ্য c] |
পিথাগোরাসের উপপাদ্যের বিপরীত উপপাদ্য
যদি কোনো ত্রিভুজের একটি বাহুর উপর অঙ্কিত বর্গক্ষেত্র অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের সমষ্টির সমান হয়, তবে শেষোক্ত বাহুদ্বয়ের অন্তর্ভুক্ত কোণটি সমকোণ হবে ।
বিশেষ নির্বচন :
মনে করি, ∆ABC এর AB2 = AC2 + BC2 প্রমাণ করতে হবে যে, ∠C = এক সমকোণ ।
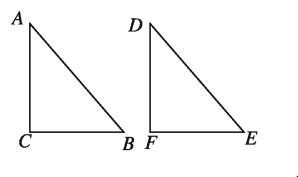
অঙ্কন :
এমন একটি ত্রিভুজ DEF আঁকি, যেন ∠F এক সমকোণ,
EF = BC এবং DF = AC হয়।
প্ৰমাণ :
|
ধাপ |
যথার্থতা |
| (1) DE2 = EF2 + DF2
= BC2 + AC2 = AB 2 DE = AB এখন ∆ABC ও ∆DEF এ BC = EF, AC = DF এবং AB =DE. ∆ABC = ∆DEF ∠C = ∠F :. ∠C = এক সমকোণ । [প্রমাণিত] |
[কারণ ∆DEF এ ∠F এক সমকোণ]
[কল্পনা] [বাহু-বাহু-বাহু সর্বসমতা [ ∠F এক সমকোণ ] |
