পূর্ণসংখ্যার যোগ । মাধ্যমিক ৬ষ্ট শ্রেণি গণিত, ২০২৩

আমাদের আজকের আলোচনার বিষয় পূর্ণসংখ্যার যোগ – যা পূর্ণসংখ্যার জগৎ এর অন্তর্ভুক্ত। গণিত হল জ্ঞানের একটি ক্ষেত্র যাতে সংখ্যা, সূত্র এবং সম্পর্কিত কাঠামো, আকার এবং সেগুলির মধ্যে থাকা স্থানগুলি এবং পরিমাণ এবং তাদের পরিবর্তনগুলি অন্তর্ভুক্ত থাকে। এই বিষয়গুলি যথাক্রমে সংখ্যা তত্ত্বের প্রধান উপশাখা,বীজগণিত, জ্যামিতি, এবং বিশ্লেষণ। তবে একাডেমিক শৃঙ্খলার জন্য একটি সাধারণ সংজ্ঞা সম্পর্কে গণিতবিদদের মধ্যে কোন সাধারণ ঐকমত্য নেই।

গণিতে সংখ্যা ও অন্যান্য পরিমাপযোগ্য রাশিসমূহের মধ্যকার সম্পর্ক বর্ণনা করা হয়। গণিতবিদগন বিশৃঙ্খল ও অসমাধানযুক্ত সমস্যাকে শৃঙ্খলভাবে উপস্থাপনের প্রক্রিয়া খুঁজে বেড়ান ও তা সমাধানে নতুন ধারণা প্রদান করে থাকেন।গাণিতিক প্রমাণের মাধ্যমে এই ধারণাগুলির সত্যতা যাচাই করা হয়। গাণিতিক সমস্যা সমাধান সম্পর্কিত গবেষণায় বছরের পর বছর, যুগের পর যুগ বা শত শত বছর পর্যন্ত লেগে যেতে পারে। গণিতের সার্বজনীন ভাষা ব্যবহার করে বিজ্ঞানীরা একে অপরের সাথে ধারণার আদান-প্রদান করেন। গণিত তাই বিজ্ঞানের ভাষা।

 

পূর্ণসংখ্যার যোগ

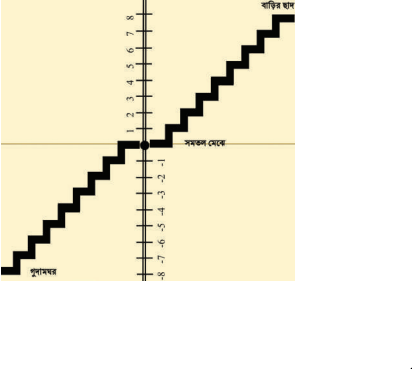
তারেকদের একতলা বাড়ির ছাদে এবং নিচের গুদামঘরে যাওয়ার জন্য একটি সিঁড়ি আছে। এবারে, বাড়ির মেঝে থেকে উপরে ওঠার প্রত্যেকটি সিঁড়ি ধনাত্মক পূর্ণ সংখ্যা, নিচে গুদামঘরে যাওয়ার জন্য প্রত্যকটি সিঁড়ি ঋণাত্মক পূর্ণ সংখ্যা এবং সমতল মেঝে শূন্য (০) নির্দেশ করে।

এখন নিচের বাক্যগুলো পড় এবং খালিঘর পূরণ করো (দুইটি করে দেখানো হলো)

(ক) সমতল মেঝে থেকে 6টি সিঁড়ি উপরে উঠলে হবে:

+6

(খ) সমতল মেঝে থেকে 5টি সিঁড়ি নিচে নেমে তারপর সেখান থেকে 7 টি সিঁড়ি উপরে উঠলে হবে:

(-5) + 7 = 2

(গ) সমতল মেঝে থেকে 4টি সিঁড়ি নিচে নামলে হবে:

(ঘ) সমতল মেঝে থেকে 2টি সিঁড়ি উপরে উঠে তারপর সেখান থেকে ওটি সিঁড়ি উপরে উঠলে হবে:

(ঙ) সমতল মেঝে থেকে 4টি সিঁড়ি নিচে নেমে তারপর সেখান থেকে আরও 2টি সিঁড়ি নিচে নামলে হবে:

(চ) সমতল মেঝে থেকে 5টি সিঁড়ি নিচে নেমে তারপর সেখান থেকে 3টি সিঁড়ি উপরে উঠলে হবে:

(ছ) সমতল মেঝে থেকে 4টি সিঁড়ি উপরে উঠে তারপর সেখান থেকে ৪টি সিঁড়ি নিচে নামলে হবে:

• দলগতভাবে সংখ্যারেখা অঙ্কন করে উপরের বর্ণিত প্রশ্নের অনুরূপ কিছু প্রশ্ন ও উত্তর তৈরি করো এবং শিক্ষকদের নির্দেশে এক দলের কাজ অন্য দলের সাথে বিনিময় ও মূল্যায়ন করো

সংখ্যারেখার সাহায্যে পূর্ণ সংখ্যার যোগ

(ক) সংখ্যারেখার সাহায্যে 3 ও 5 এর যোগ অর্থাৎ 3 + 5 নির্ণয়:

 

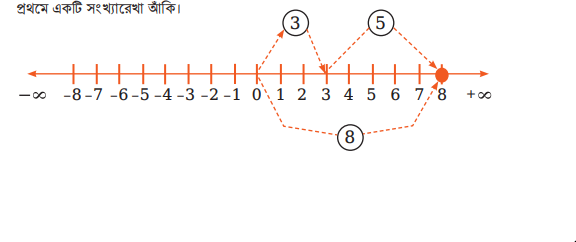সংখ্যারেখার ০ বিন্দু থেকে ডান দিকে প্রথমে 3 ধাপ অতিক্রম করে 3 বিন্দুতে পৌঁছাই। তারপর 3 বিন্দুর ডান দিকে আরও 5 ধাপ অতিক্রম করি এবং ৪ বিন্দুতে পৌঁছাই। তাহলে 3 ও 5 এর যোগফল হবে 3 + 5 = 8

(খ) সংখ্যারেখার সাহায্যে 5 ও-3 এর যোগ অর্থাৎ (-5) + (-3) নির্ণয়:

প্রথমে একটি সংখ্যা সংখ্যারেখা আঁকি।

 

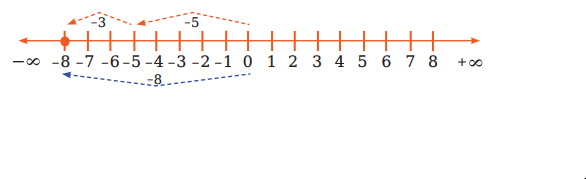
সংখ্যারেখার উপর ০ বিন্দু থেকে বাম দিকে প্রথমে 5 ধাপ অতিক্রম করে -5 বিন্দুতে পৌঁছাই। তারপর -5 বিন্দুর বাম দিকে আরও 3 ধাপ অতিক্রম করি এবং ৪ বিন্দুতে পৌঁছাই। তাহলে -5 ও -3 এর যোগফল হবে (-5)+(-3)=-8

(গ) সংখ্যারেখার সাহায্যে 5 ও-3 এর যোগ অর্থাৎ 5+ (-3) নির্ণয়:

প্রথমে একটি সংখ্যারেখা আঁকি।

 

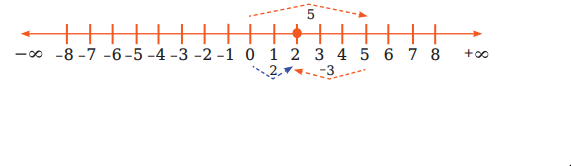
সংখ্যারেখার উপর ০ বিন্দু থেকে ডান দিকে প্রথমে 5 ধাপ অতিক্রম করে 5 বিন্দুতে পৌঁছাই। তারপর 5 বিন্দুর বাম দিকে 3 ধাপ অতিক্রম করি এবং 2 বিন্দুতে পৌঁছাই। তাহলে 5 ও -3 এর যোগফল হবে (+5) + (-3) = 2

(ঘ) সংখ্যারেখার সাহায্যে -5 ও 3 এর যোগ অর্থাৎ (-5) + 3 নির্ণয়:

প্রথমে একটি সংখ্যারেখা আঁকি।

 

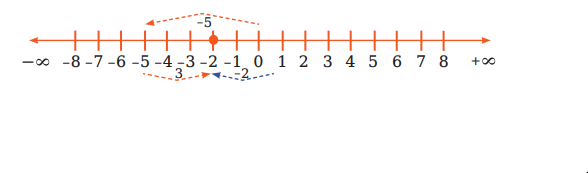সংখ্যারেখার উপর ০ বিন্দু থেকে বাম দিকে প্রথমে 5 ধাপ অতিক্রম করে -5 বিন্দুতে পৌঁছাই। তারপর -5 বিন্দুর ডান দিকে ও ধাপ অতিক্রম করি এবং 2 বিন্দুতে পৌঁছাই। তাহলে -5 ও 3 এর যোগফল হবে (-5) + (3)-2

উপরের আলোচনা থেকে আমরা দেখতে পাই যে:

যদি কোনো পূর্ণ সংখ্যার সাথে একটি ধনাত্মক পূর্ণ সংখ্যার যোগ করা হয় তবে যোগফল পূর্ণসংখ্যাটি থেকে বড় হয়।

আবার, যদি কোনো পূর্ণসংখ্যার সাথে একটি ঋণাত্মক পূর্ণসংখ্যা যোগ করা হয় তবে যোগফল পূর্ণসংখ্যাটি থেকে ছোট হয়।

এখন দুইটি পূর্ণ সংখ্যা ও ও-3 এর যোগফল নির্ণয় করি প্রথমে সংখ্যারেখার উপর ০ বিন্দু থেকে ডান দিকে 3 ধাপ অতিক্রম করে +3 বিন্দুতে পৌঁছাই এবং তারপরে +3 বিদু থেকে বাম দিকে 3 ধাপ অতিক্রম করি। তাহলে আমরা কোন বিন্দুতে পৌছালাম?

উপরের চিত্র থেকে দেখতে পাই যে,+ 3+ (-3) = 0 অর্থাৎ 0 বিন্দুতে পৌছালাম। সুতরাং দুইটি পূর্ণসংখ্যা + 3 ও (-3) যোগ করলে আমরা পাই শূন্য অর্থাৎ একটি ধনাত্মক পূর্ণ সংখ্যার সাথে তার ঋণাত্মক পূর্ণসংখ্যা যোগ করলে যোগফল শূন্য হয়।

এক্ষেত্রে -3 কে +3 এর যোগাত্মক বিপরীত এবং +3 কে-3 এর যোগাত্মক বিপরীত বলা হয়। কাজ:

১) কয়েকটি ধনাত্মক ও ঋণাত্মক পূর্ণসংখ্যা লিখে তাদের যোগাত্মক বিপরীত সংখ্যা লেখো এবং এগুলোকে সংখ্যারেখায় দেখাও।

২) সংখ্যারেখা ব্যবহার করে নিচের যোগফল নির্ণয় করো:

৩) এধরনের আরও দুইটি প্রশ্ন তৈরি করো এবং নিজে নিজে সংখ্যা রেখা ব্যবহার করে সমাধান করো

দুইয়ের বেশি পূর্ণসংখ্যার যোগফল নির্ণয়

তোমরা এতক্ষণ দেখেছ কীভাবে দুইটি পূর্ণসংখ্যার যোগফল নির্ণয় করা যায়।

চলো তাহলে এই ধারণা ব্যবহার করে দুইয়ের বেশি পূর্ণসংখ্যার যোগফল নির্ণয় করার চেষ্টা করি।

• আমরা শুরুতে – 9, + 4 এবং -6 এই তিনটি পূর্ণসংখ্যার যোগফল অর্থাৎ (-6-) + (4+) + (9) এর মান নির্ণয় করব।

সমাধান: প্রদত্ত রাশিমালার ঋণাত্মক সংখ্যাগুলোকে একত্রে পাশাপাশি সাজিয়ে লিখে পাই,

(-9)+(+4) + (-6)

= (-9)+(-6) + (+4) =

=(-15) +(+4)

=-15+4

= -11

• এবার আমরা -63, -23, +30 এবং +55 এই চারটি পূর্ণসংখ্যার যোগফল অর্থাৎ (+55) + (-63) + (-23) + (+30) এর মান নির্ণয় করব।

পাই,

(+30)+(-23) + (-63) + (+55)

= (+30)+(+55)+(-23)+(-63)

= (-63)+(-23)+(+30)+(+55)

=(+85)+(-86)

= 85-86

=-1