আজকে আমরা অনুপাত, সদৃশতা ও প্রতিসমতার অনুশীলনী ১ আলোচনা করবো। এটি নবম – দশম শ্রেনী গণিতের অনুপাত, সদৃশতা ও প্রতিসমতার অন্তর্গত।

অনুপাত, সদৃশতা ও প্রতিসমতার অনুশীলনী ১
দুইটি রাশির তুলনা করার জন্য এদের অনুপাত বিবেচনা করা হয়। অনুপাত নির্ণয়ের জন্য রাশি দুইটি একই এককে পরিমাপ করতে হয়।
১. কোনো ত্রিভুজের ভূমি সংলগ্ন কোণদ্বয়ের সমদ্বিখণ্ডকদ্বয় বিপরীত বাহু দুইটিকে X ও Y বিন্দুতে ছেদ করে। XY, ভূমির সমান্তরাল হলে প্রমাণ কর যে, ত্রিভুজটি সমদ্বিবাহু।
২. প্রমাণ কর যে, কতকগুলো পরস্পর সমান্তরাল সরলরেখাকে দুইটি সরলরেখা ছেদ করলে অনুরূপ অংশগুলো সমানুপাতিক হবে।
৩. প্রমাণ কর যে, ট্রাপিজিয়ামের কর্ণদ্বয় এদের ছেদবিন্দুতে একই অনুপাতে বিভক্ত হয়।
৪. প্রমাণ কর যে, ট্রাপিজিয়ামের তির্যক বাহুদ্বয়ের মধ্যবিন্দুর সংযোজক রেখাংশ সমান্তরাল বাহুদ্বয়ের সমান্তরাল।

৫. ABC ত্রিভুজের AD ও BE মধ্যমাদ্বয় পরস্পর G বিন্দুতে ছেদ করেছে। G বিন্দুর মধ্য দিয়ে অঙ্কিত DE এর সমান্তরাল রেখাংশ AC কে F বিন্দুতে ছেদ করে । প্রমাণ কর যে, AC = 6EF
৬. ∆ABC এর BC বাহুস্থ যেকোনো বিন্দু X এবং AX রেখাস্থ O একটি বিন্দু। প্রমাণ কর যে, ∆AOB: ∆AOC = BX : XC
৭. ∆ABC এর ∠A এর সমদ্বিখণ্ডক BC কে D বিন্দুতে ছেদ করে। BC এর সমান্তরাল কোনো রেখাংশ AB ও AC কে যথাক্রমে E ও F বিন্দুতে ছেদ করে। প্রমাণ কর যে, BD : DC = BE : CF
৮. ABC ও DEF সদৃশকোণী ত্রিভুজদ্বয়ের উচ্চতা AM ও DN হলে প্রমাণ কর যে, AM : DN = AB : DE
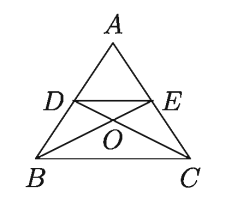
৯. পাশের চিত্রে BC || DE
ক) প্রমাণ কর ∆BOC ও ∆DOE সদৃশ।
খ) প্রমাণ কর, AD: BD = AE : CE
গ) প্রমাণ কর, BO : OE = CO : OD
