আজকের আলোচনার বিষয়ঃ ফাংশনের অন্বয় । যা উচ্চতর গণিতের সেট ও ফাংশন অংশের অন্তর্গত।
যা দ্বারা দুই বা ততোধিক চলকের মধ্যে অথবা, দুইটি সেটের মধ্যে সম্পর্ক বুঝানো হয় তাকে অন্বয় বলে। অথাৎ A ও B সেট হলে A×B এর কোন অশূণ্য উপসেটকে A থেকে B তে একটি অন্বয় বলা হয় । অর্থাৎ যদি S, A থেকে B তে একটি অন্বয় হয় তবে, S = {(x,y) ∣ x ∈ A, y ∈ B}
আবার, A×A এর কোন অশূণ্য উপসেটকে A সেটে একটি অন্বয় বলে ।
ফাংশনের অন্বয়
অনেক সময় আমরা সেট X এর উপাদানগুলোর মধ্যে অথবা সেট X ও সেট Y এর উপাদানগুলোর মধ্যে বিভিন্ন সম্পর্ক বিবেচনা করি। যেমন, স্বাভাবিক সংখ্যার সেট N এ বড়-ছোট সম্পর্ক, কোনো পরিবারে ভাই-বোন সম্পর্ক, তোমার শ্রেণির শিক্ষার্থীদের সঙ্গে সর্বশেষ জন্মদিনে তাদের বয়সের সম্পর্ক।
উদাহরণ ১৮.
মনে করি A = {0,1,2,3} একটি সেট। A সেটের উপাদানগুলোর মধ্যে x < y সম্পর্কটিকে A × A এর উপসেট S = { (0,1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)} দ্বারা বর্ণনা করা যায়, যেখানে S সেটের অন্তর্ভুক্ত ক্রমজোড় গুলোর (প্রথম অংশক) < (দ্বিতীয় অংশক)। এক্ষেত্রে S হলো A সেটে বর্ণিত < অন্বয়।
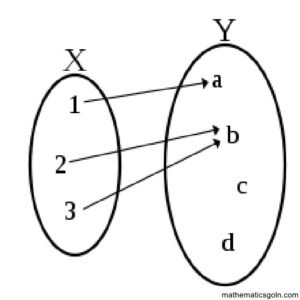
উদাহরণ ১৯.
মনে করি কোনো পরিবারে a. পিতা, ৮ মাতা, c বড় ছেলে, d ছোট ছেলে, মেয়ে, f বড় ছেলের স্ত্রী। পরিবারের সদস্যদের সেটকে F ধরে আমরা পাই F { a, b, c, d, e, f} । F সেটে = ভাই সম্পর্ক অর্থাৎ æ হলো y এর ভাই সম্পর্কটিকে B = { (c, d), (c, e), (d, c), (d,e)} দ্বারা বর্ণনা করা যায়, যেখানে B সেটের অন্তর্ভুক্ত ক্রমজোড়গুলোর প্রথম অংশক হলো দ্বিতীয় অংশকের ভাই। B সেট হলো F সেটে ভাই অন্বয়।

সংজ্ঞা ৪ (অন্বয়).
X ও Y সেট হলে এদের কার্তেসীয় গুণজ সেট X X Y এর যেকোনো উপসেটকে X হতে Y এ একটি অন্বয় বলা হয়। অর্থাৎ R⊆ X × Y হলো X হতে Y এ বর্ণিত অন্বয়।
ফাংশন: গাণিতিক সমস্যা ঃ

১ thought on “ফাংশনের অন্বয়”