আজকে আমরা আলোচনা করবো অন্বয় ও ফাংশনের লেখচিত্র । যা উচ্চতর গণিতের সেট ও ফাংশন অংশের অন্তর্গত।
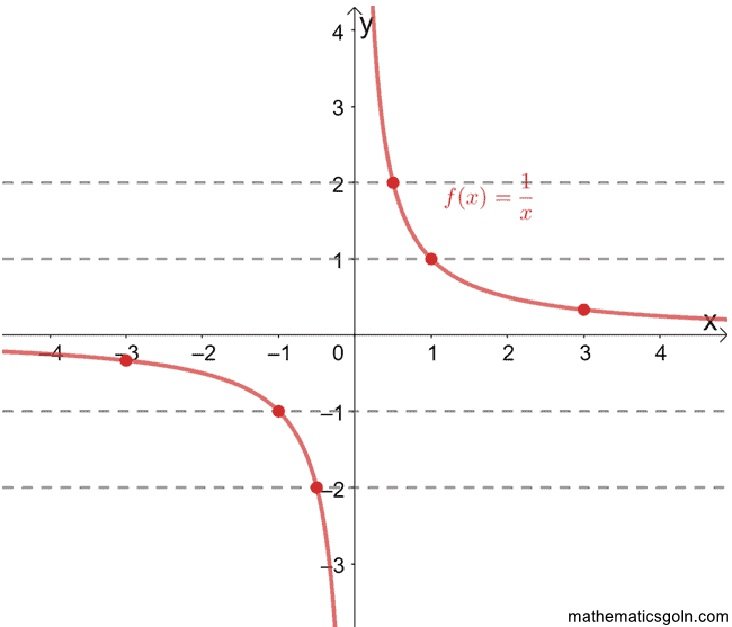
অন্বয় ও ফাংশনের লেখচিত্র
লেখচিত্র হলো ফাংশনের জ্যামিতিক উপস্থাপন। if(x) লেখচিত্র অঙ্কনের জন্য O বিন্দুতে = পরস্পর ছেদী লম্ব দুইটি সরলরেখা XOX’ এবং YOY’ নেওয়া হয়। O কে মূলবিন্দু, XOX’ কে অক্ষ এবং YOY’ কে y অক্ষ বলা হয়।
y = f(x) ফাংশনের লেখচিত্র অঙ্কনের জন্য a ≤ x ≤ b ব্যবধিতে স্বাধীন চলক x এবং অধীন চলক y এর মানগুলোর তালিকা প্রস্তুত করতে হয়। অত:পর তালিকার সীমিত সংখ্যক বিন্দুগুলোকে xy সমতলে স্থাপন করতে হয়। প্রাপ্ত বিন্দুগুলোকে সরলরেখা অথবা বক্ররেখা দ্বারা যুক্ত করলে y = f(x) ফাংশনের লেখচিত্র পাওয়া যায়। নবম-দশম শ্রেণির গণিতে লেখচিত্র সম্পর্কে প্রাথমিক ধারণা প্রদান করা হয়েছে। এখানে, সরলরৈখিক (Linear) ফাংশন, দ্বিঘাত (Quadratic) ফাংশন এবং বৃত্তের লেখচিত্র অঙ্কন সম্পর্কে আলোচনা করা হয়েছে।
সরলরৈখিক ফাংশন
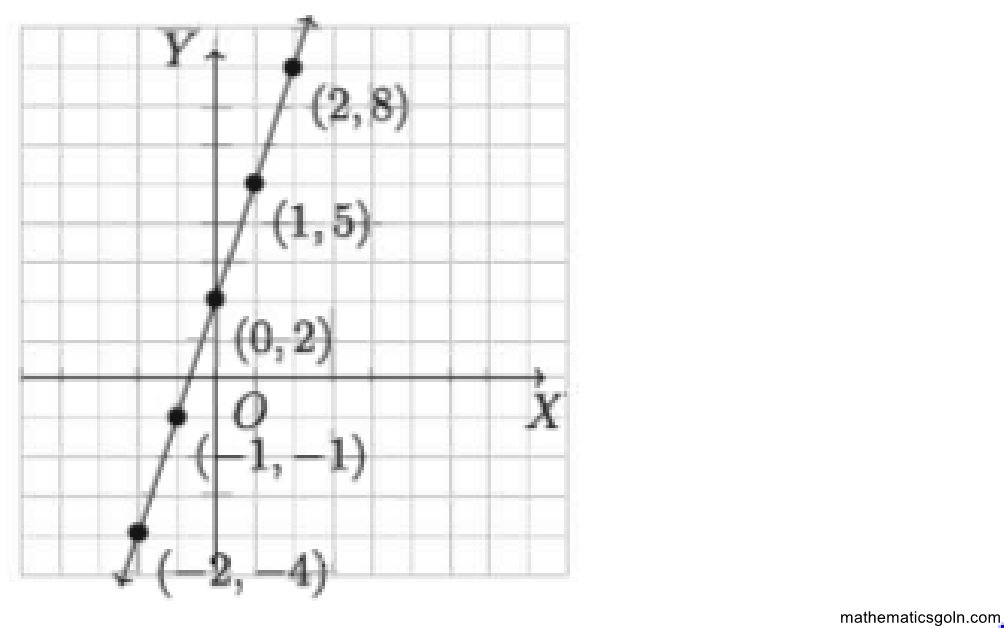
সরলরৈখিক ফাংশন এর সাধারণ রূপ হলো f(x) = mx + b যেখানে, m এবং b বাস্তব সংখ্যা। এর লেখচিত্র একটি রেখা যার ঢাল হলো m এবং y অক্ষের ছেদক b
এখানে, ধরি m 3 এবং b = 2 তাহলে = ফাংশনটি দাঁড়ায় f(x) = 3x + 2
বর্ণিত ফাংশন হতে x ও y এর নিম্নরূপ সংশ্লিষ্ট মান পাওয়া যায়:
ফাংশনটির লেখ পাশে দেখানো হলো।
দ্বিঘাত ফাংশন (Quadratic Function)
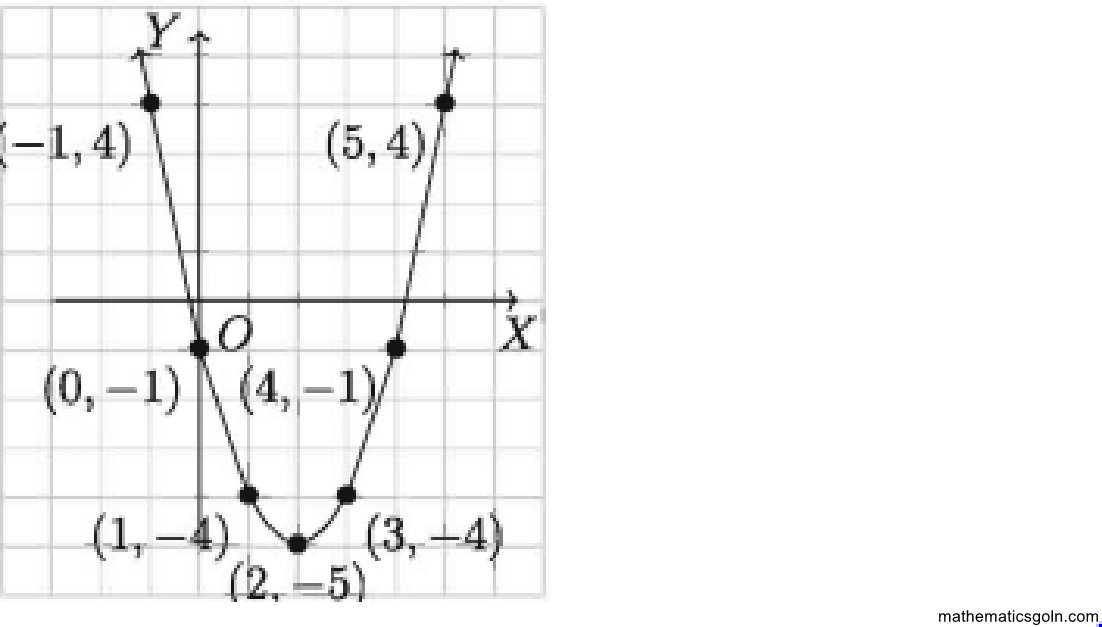
দ্বিঘাত ফাংশন হলো একটি ফাংশন যা y = ax2 + b + c সমীকরণ দ্বারা বর্ণিত যেখানে a, b ও c বাস্তব সংখ্যা এবং a ≠ 0। প্রদত্ত ফাংশনে ধরি a b −4, c = −1। তাহলে a = y = ax2 + bc + c কে লেখা যায় y = x2 – 4x – 1। বর্ণিত ফাংশন হতে x ও y এর সংশ্লিষ্ট মান পাওয়া যায় যা নিচের সারণিতে দেখানো হয়েছে।
উপরে দ্বিঘাত ফাংশনটির লেখচিত্র। এই দ্বিঘাত ফাংশন এর কিছু সাধারণ বৈশিষ্ট্য লক্ষ করি।
ক) লেখচিত্রটি পরাবৃত্ত আকারের।
খ) লেখচিত্রটির y অক্ষের সমান্তরাল রেখা বা y অক্ষ বরাবর প্রতিসাম্য বিন্দু পাওয়া যাবে।
গ) একটি বিন্দুতে ফাংশনটির মান ক্ষুদ্রতম বা বৃহত্তম হবে।
বৃত্তের লেখচিত্র
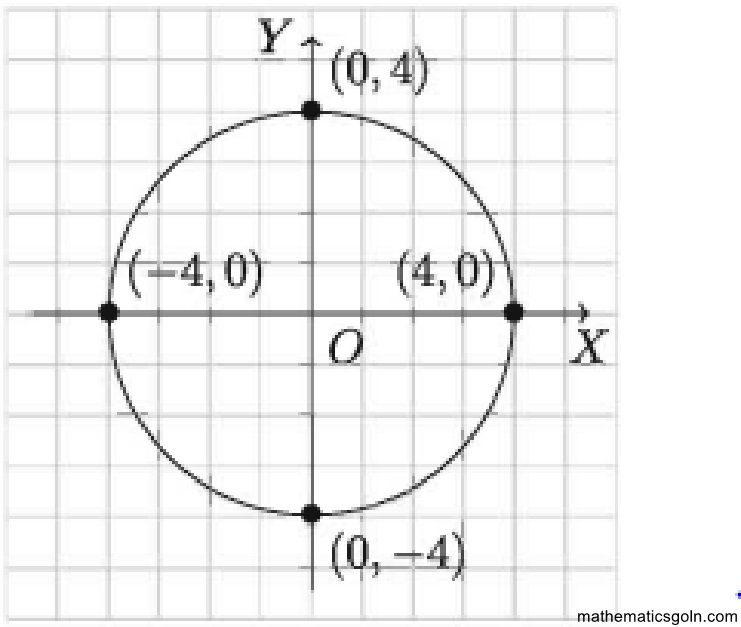
উল্লেখ্য যে p,q ও r ধ্রুবক এবং r ≠ 0 হলে R এ S = {(x, y) (x – p) 2 + (y – q)2 = r2} : – অন্বয়ের লেখ একটি বৃত্ত যার কেন্দ্র (p, g) এবং ব্যাসার্ধ । (নবম-দশম শ্রেণির গণিত দ্রষ্টব্য)। ছক কাগজে (p,q) বিন্দু পাতন করে ঐ বিন্দুকে কেন্দ্র করে ” ব্যাসার্ধ নিয়ে বৃত্ত অঙ্কন করে লেখচিত্রটি পাওয়া যায়।
মন্তব্য:
যে অন্বয়ের সমাধান সেট অসীম, এর লেখচিত্র অঙ্কনের স্বীকৃত পদ্ধতি হলো যথেষ্ট সংখ্যক সমাধানের প্রতিরূপী বিন্দু ছক কাগজে পাতন করে সাবলীলভাবে ঐ সব বিন্দু যোগ করা, যাতে অন্বয়টির লেখচিত্রের ধরন দ্ব্যর্থহীনভাবে বুঝা যায়। কিন্তু যে অন্বয়ের লেখচিত্র বৃত্ত, এর জন্য কম্পাস ব্যবহার করলে কাজ সহজ ও সুন্দর হয় বিধায় শেষোক্ত পদ্ধতি অবলম্বন করা হলো ।

উদাহরণ ৩৫.
S = {(x, y) : x2 + y2 = 16}
সুতরাং S এর লেখচিত্র একটি বৃত্ত, x2 + y2 = 42 যার কেন্দ্র (0, 0) এবং ব্যাসার্ধ r = 4।
S এর লেখচিত্র নিম্নে দেখানো হলঃ
উদাহরণ ৩৬.
দেওয়া আছে,
দেওয়া আছে, f : x (2x-1)/( 2x+3)
ক) f (-⅓)= কত?
খ) ফাংশনটি এক-এক কিনা তা নির্ধারণ কর।
গ) 2f – 1 (x) = x হলে x এর মান নির্ধারণ কর।
সমাধান :
ক) দেওয়া আছে, f : x →(2x 1)/ (2x+3 )
সুতরাং f(x) = (2x 1)/ (2x+3 )
খ) দেওয়া আছে, f : x →(2x 1)/ (2x+3 ) ।
সুতরাং f(x) = (2x 1)/ (2x+3 )
এখানে 2x + 3 = 0 হলে অর্থাৎ x = −3/2 হলে, ফাংশনটি অসংজ্ঞায়িত হয়।
x ≠-3/2, সুতরাং ডোমƒ = R\ {-3/2}
ধরি, x1 ∈ ডোম f এবং x2 ∈ ডোম f
f(x1): = (2×1-1)/ (2×1+3) এবং f(x2) = (2×2-1)-( 2×2 +3)
এখন f(x1) = f(x2) হবে, যদি ও কেবল যদি
(2×1-1)/ (2×1+3) = (2×2-1)-( 2×2 +3)
বা, (2×1-1)/ (2×1+3) = (2×2-1)-( 2×2 +3) -1
বা, (2×1-1-2×1-3)/ 2×1+3=(2×2-1-2×2-3) /2×2 +3
বা, -4 /(2×1 +3 )= -4 /(2×2 +3)
2×1+3=2×2 +3
2×1 = 2×2
বা x1 = x2 হয়।
ফাংশনটি এক-এক ফাংশন।
গ) দেওয়া আছে,
f : x →(2x-1)/( 2x + 3)
সুতরাং f(x) = (2x-1)/( 2x + 3)
ধরি, f(x) = y
x = ƒ-¹(y)
এখন, f(x) = (2x-1)/( 2x + 3)
বা, y = (2x-1)/( 2x + 3)
বা, 2xy +3y=2x-1
বা, 2xy – 2x = -3y-1
বা,-2x(1- y) = -(1+3y)
বা, x = (1+ 3y)/ 2(1-y)
বা, f-2(y) = (1+3y)/ 2(1- y) [: x = f-1(y)]
বা, f-1(x) = (1+ 3x)/2(1-x)[চলক পরিবর্তন করে]
2f-1(x) = (1+ 3x)/ (1-x)
বা, x = (1+ 3x)/ (1-x) [2ƒ-1(x) = x]
বা,1+ 3x =x-x2 ,
বা, 1+3x=x-x2
বা, x²+3x-x+1=0
বা, x²+2x+1=0
বা, (x+1)² = 0
বা, x + 1 = 0 বা, x = −1
নির্ণয় মান, x = -1

১ thought on “অন্বয় ও ফাংশনের লেখচিত্র”