বিপরীত ফাংশন

আজকে আমরা আলোচনা করবো  সেট প্রক্রিয়ার কতিপয় প্রতিজ্ঞা সম্পর্কে । যা উচ্চতর গণিতের সেট ও ফাংশন অংশের অন্তর্গত।

 

 

বিপরীত ফাংশন

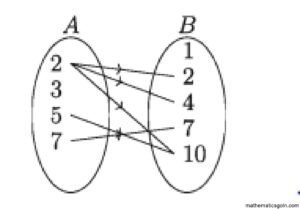
নিচের তিনটি চিত্রে তিনটি ফাংশন বর্ণনা করা হয়েছে।

ক) উপরের বামের চিত্রের ফাংশনটির অধীনে a → 1, b → 2, c → 4 । এই ফাংশনটি এক-এক কিন্তু সার্বিক নয় কেননা 3 এর কোনো প্রাক প্ৰতিবিম্ব নেই।

খ) উপরের মাঝের চিত্রের ফাংশনটির অধীনে a →1,b → 2,c → 2। এই ফাংশনটি সার্বিক কিন্তু এক-এক নয় কেননা b ও c এর প্রতিবিম্ব 2।

গ) উপরের ডানের চিত্রের ফাংশনটির অধীনে a 2, b 1, c 3। এই ফাংশনটি এক-এক ও সার্বিক। শেষোক্ত ক্ষেত্রে কোডোমেন D এর প্রত্যেক উপাদানের জন্য ডোমেন A এর একটি ও কেবল একটি উপাদান নির্দিষ্ট হয়েছে। ফলে, D হতে A তে একটি ফাংশন বর্ণিত হয়েছে, যেই ফাংশনকে প্রদত্ত ফাংশনের বিপরীত ফাংশন বলা হয়।

 

 

 

সংজ্ঞা ৯ (বিপরীত ফাংশন).

মনে করি, f : A→ B একটি এক-এক ও সার্বিক ফাংশন। একটি ফাংশন g : B → A বর্ণিত হয় যেখানে প্রত্যেক b∈ B এর জন্য g (b) = a যদি ও কেবল যদি f(a) = b হয়। এই ফাংশন g কে f এর বিপরীত ফাংশন বলা হয় এবং f−1 দ্বারা নির্দেশ করা হয় অর্থাৎ g = f-1।

উপরের ডানের চিত্রে বর্ণিত ফাংশনটি f হলে f-1 : D → A এবং f−1(1) = b, f−1 (2) = a, f−1(3) = c। উপরের অন্য দুইটি চিত্রে বর্ণিত ফাংশন দুইটির বিপরীত ফাংশন সম্ভব নয়।

উদাহরণ ২৪.

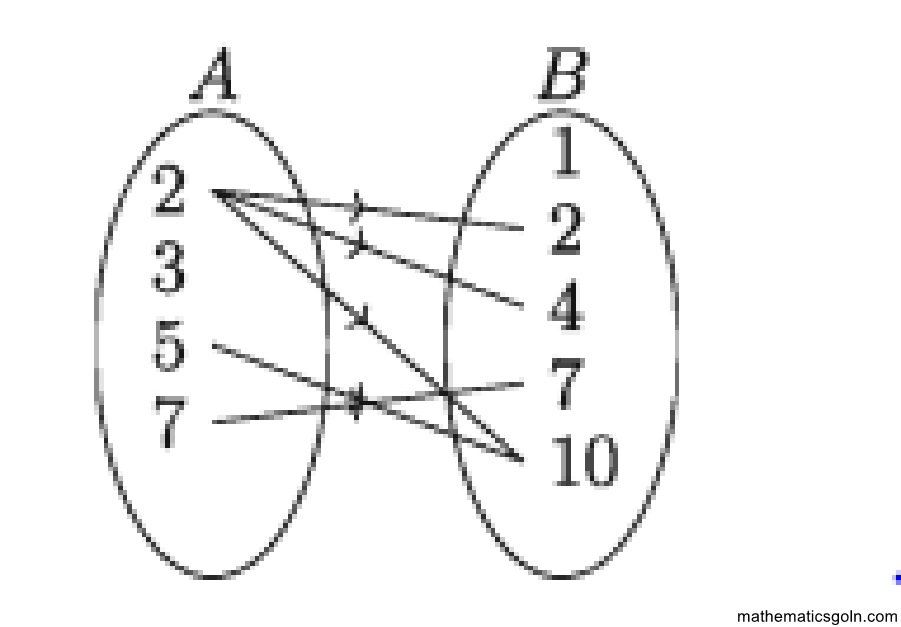
মনে করি, A {2, 3, 5, 7} এবং B = {1, 2, 4, 7, 10} । A এর যে যে সদস্য = দ্বারা B এর যে যে সদস্য বিভাজ্য হয় এদেরকে নিচের চিত্রে তীর চিহ্নিত করে দেখানো হলো:

এখানে D = {(2, 2), (2, 4), (2, 10), ( 5, 10 ), ( 7, 7 ) } এরূপ অন্বিত সদস্যদের দ্বারা গঠিত = ক্রমজোড়গুলোর সেট, যা দ্বারা এই বিভাজ্যতা সম্পর্কটি বর্ণনা করা যায়। D সেটে অন্তর্ভুক্ত ক্রমজোড়গুলোর প্রথম অংশ A এর সদস্য ও দ্বিতীয় অংশ B এর সদস্য যেখানে প্রথম অংশ দ্বারা দ্বিতীয় অংশ বিভাজ্য। অর্থাৎ, DC Ax B এবং D {(x, y) : x ∈ A, y ∈ B এবং দ্বারা বিভাজ্য}, এখানে D সেটটি A সেট থেকে B সেটে একটি অন্বয়।

 

 

উদাহরণ ২৫.

বাস্তব সংখ্যার ক্রমজোড়ের সেট L = {(x, y) : x ∈ R, y ∈ R এবং x < y} বিবেচনা করি। দুইটি বাস্তব সংখ্যা a, b এর জন্য a < b যদি ও কেবল যদি (a,b) ∈ L হয়। সুতরাং L সেট দ্বারা বাস্তব সংখ্যার ছোট-বড় সম্পর্ক বর্ণিত হয়।

উদাহরণ ২৬

নিচের কোন অন্বয়টি (relation) ফাংশন নয়? যুক্তি দাও।

সমাধান:

উপরের বাম পাশের সম্পর্কটি ফাংশন নয় কারণ 2 4, 25 এবং 3 4 3 5 1 বাকি তিনটি সম্পর্কই ফাংশন।

উদাহরণ ২৭.

f : æ → 2×2 + 1 ফাংশনের রেঞ্জ নির্ণয় কর যেখানে ডোমেন X = {1,2,3}।

সমাধান:

f(x) = 2x² + 1 যেখানে x ∈ X
ƒ(1) = 2(1)² + 1 = 3, ƒ(2) = 2(2)² + 1 = 9 এবং ƒ(3) = 2(3)² + 1 = 191

{1, 2, 3} এর রেঞ্জ সেট

= {3, 9, 19} |

উদাহরণ ২৮.

তাহলে নির্ণয় কর: f : * → mx + c ফাংশনের জন্য 2 এবং 4 এর প্রতিবিম্ব যথাক্রমে 7 ও – 1।

ক) m এবং c এর মান।

খ) f এর অধীনে 5 এর প্রতিবিম্ব।

গ) f এর অধীনে 3 এর প্রাক প্রতিবিম্ব।

 

 

সমাধান :

ক) f(x) = mx + c এ দেওয়া আছে
f : 2 → 7 অর্থাৎ f(2) = 7 বা, 2m + c = 7 ……(1)
f : 4 → -1 অর্থাৎ f(4) = − 1 বা, 4m + c = -1……(2)

(1) ও (2) থেকে পাই m = –4 এবং c = 15

খ) f এর অধীনে 5 এর প্রতিবিম্ব f (5) = 4 × 5 + 15 = –5

গ) 3 এর প্রাক প্রতিবিম্ব x হলে f(x) = 3 অর্থাৎ – 4x + 15 = 3 বা x = 3

কাজ:

F = {(−2, 4), (–1, 1), (0, 0 ), (1, 1), (2, 4)} অন্বয়টি কী ফাংশন? এর ডোমেন ও রেঞ্জ নির্ণয় কর। সম্ভব হলে F এর জন্য একটি সূত্র নির্ণয় কর।

মন্তব্য:

কোনো ফাংশন F’ এর ডোমেন এবং ডোমেনের প্রত্যেক সদস্য : এর অনন্য প্রতিবিম্ব F(2) নির্দিষ্ট করা হলেই ফাংশনটি নির্ধারিত হয়। অনেক সময় ডোমেন উহ্য রাখা হয়। এরূপ ক্ষেত্রে ডোমেন হিসেবে ঐ সেটকে গ্রহণ করা হয়, যার প্রত্যেক উপাদানের জন্য F(x) নির্ধারিত থাকে।

 

 

উদাহরণ ২৯.

F(x) √1 x দ্বারা বর্ণিত ফাংশনের ডোমেন নির্ণয় কর। F(−3), F(0), = * (2), F(1), F(2) এর মধ্যে যেগুলো সংজ্ঞায়িত সেগুলো নির্ণয় কর।

সমাধান:

F(x) = √1 − x ∈ R যদি ও কেবল যদি 1 − x ≤ 0 বা 1 ≤ x অর্থাৎ, x ≤ 1 – সুতরাং ডোম F = {x : x ∈ R এবং x ≤ 1 }

= F(-3)= √{1 − (−3)} = √4 = 2
F(0)=√(1-0)=√1=1

F (½)= √ 1-(½) = √(½) = 1/√2

F(1) = √1-1=0

F(2) সংজ্ঞায়িত নয়, কেননা 2 ¢ ডোম F।