আজকে আমাদের আলোচনার বিষয়ঃ বীজগণিতীয় সূত্রাবলি । এটি অষ্টম শ্রেনী গণিতের বীজগণিতীয় সূত্রাবলি ও প্রয়োগের অন্তর্গত।

বীজগণিতীয় সূত্রাবলি
সপ্তম শ্রেণিতে বীজগণিতীয় প্রথম চারটি সূত্র ও এদের সাথে সম্পৃক্ত অনুসিদ্ধান্তগুলো সম্বন্ধে আলোচনা করা হয়েছে । এখানে সেগুলো পুনরুল্লেখ করা হলো ।
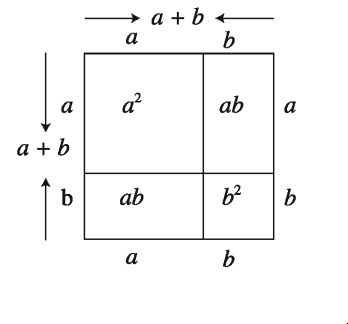
(a + b)2 এর জ্যামিতিক ব্যাখ্যাটি নিম্নরূপ :
সম্পূর্ণ বর্গক্ষেত্রটির ক্ষেত্রফল = (a + b) x (a + b) = (a + b)2
(a + b)2 = a x (a + b) x b x (a + b)
= a2 + ab + ab + b2 = a2 + 2ab + b2
আবার, বর্গক্ষেত্রটির অংশগুলোর ক্ষেত্রফলের সমষ্টি
a×a+a×b+b×a+b×b
= a2 + ab + ab + b2
= a2 + 2ab + b2
লক্ষ করি, সম্পূর্ণ বর্গক্ষেত্রটির ক্ষেত্রফল = বর্গক্ষেত্রটির অংশগুলোর ক্ষেত্রফলের সমষ্টি
(a + b) 2 = a2 + 2ab + b2
সপ্তম শ্রেণিতে যে সূত্র ও অনুসিদ্ধান্তগুলো সম্পর্কে জেনেছি তা হলো :
সূত্র ১।
(a + b) 2 = a2 + 2ab + b2
কথায়, দুইটি রাশির যোগফলের বর্গ = ১ম রাশির বর্গ + ২ × ১ম রাশি x ২য় রাশি + ২য় রাশির বর্গ ।
সূত্র ২।
(a – b) 2 = a2 – 2ab + b2
কথায়, দুইটি রাশির বিয়োগফলের বর্গ = ১ম রাশির বর্গ – ২ × ১ম রাশি x ২য় রাশি + ২য় রাশির বর্গ ।
সূত্র ৩।
a2 – b2 = (a + b) (a – b)
কথায়, দুইটি রাশির বর্গের বিয়োগফল = রাশি দুইটির যোগফল × রাশি দুইটির বিয়োগফল
সূত্র 8 ।
(x + a) (x + b) = x2 + (a + b) x + ab
কথায়, দুইটি দ্বিপদী রাশির প্রথম পদ একই হলে, তাদের গুণফল হবে প্রথম পদের বর্গ, স্ব-স্ব চিহ্নযুক্ত দ্বিতীয় পদদ্বয়ের সমষ্টির সাথে প্রথম পদের গুণফল ও স্ব-স্ব চিহ্নযুক্ত দ্বিতীয় পদদ্বয়ের গুণফলের সমষ্টির সমান।
অর্থাৎ, (x + a)(x + b) = x2 + (a এবং b এর বীজগণিতীয় যোগফল) x + (a এবং b এর গুণফল)

অনুসিদ্ধান্ত ১ ।
a2 + b2 = (a + b) 2 – 2ab
অনুসিদ্ধান্ত ২।
a2 + b2 = (a – b) 2 + 2ab
অনুসিদ্ধান্ত ৩ ।
(a + b)2 = (a – b) 2 + 4ab
অনুসিদ্ধান্ত ৪।
(a – b)²= (a + b)² – 4ab
অনুসিদ্ধান্ত ৫।
2(a² + b²) = (a + b)² + (a – b)²
অনুসিদ্ধান্ত ৬।
4ab = (a + b)² – (a – b)2
বা, ab={(a+b)/2}² – {(a-b)/2}²
উদাহরণ ১।
3x + 5y এর বর্গ নির্ণয় কর ।
সমাধান :
(3x+5y)² = (3x)² + 2 × 3x × 5y + (5y)²
=9x²+30xy+25у2
উদাহরণ ২।
বর্গের সূত্র প্রয়োগ করে 25 এর বর্গ নির্ণয় কর ।
সমাধান :
(25) 2 = (20 + 5) 2 = (20) 2 + 2 × 20 × 5 + (5) 2 = 400 + 200+ 25 = 625

উদাহরণ ৩।
4x – 7y এর বর্গ নির্ণয় কর ।
সমাধান :
(4x – 7y)2 = (4x) 2 – 2 × 4x × 7y + (7y)2 = 16×2 – 56xy + 49y2
উদাহরণ ৪।
a + b = 8 এবং ab = 15 হলে, a2 + b2 এর মান নির্ণয় কর ।
সমাধান :
a2 + b2 = (a + b) 2 – 2ab
= ( 8 ) 2 – 2 x 15
= 64 – 30
= 34
উদাহরণ ৫।
a–b = 7 এবং ab = 60 হলে, a2 + b2 এর মান নির্ণয় কর ।
সমাধান :
a2 + b2 = (a – b) 2 + 2ab
= (7) 2 + 2 × 60
= 49 + 120
= 169
উদাহরণ ৬।
x – y = 3 এবং xy= 10 হলে, (x + y)2 এর মান নির্ণয় কর।
সমাধান :
(x + y)² = (x − y)² + 4xy = (3)² + 4 × 10
= 9 +40
= 49
উদাহরণ ৭।
a + b = 7 এবং ab = 10 হলে, (a – b)2 এর মান নির্ণয় কর ।
সমাধান :
(a – b)²= (a + b)²-4ab
= (7)² – 4 × 10
= 49-40
= 9

উদাহরণ ৮।
x-1/x =5 হলে, (x+1/x )2 এর মান নির্ণয় কর ।
সমাধান :
(x+1/x )2 = (x-1/x )2 + 4 . x .1/x
=(5)²+4
=25+4
=29
উদাহরণ ৯ ।
সূত্রের সাহায্যে 3p + 4 কে 3p – 4 দ্বারা গুণ কর ।
সমাধান : ( 3p + 4 ) ( 3p – 4 ) = ( 3p ) 2 – ( 4 ) 2 [ :: (a + b) (a – b) = a2b2]
= 9p2 – 16
উদাহরণ ১০ ।
সূত্রের সাহায্যে 5m + 8 কে 5m + 9 দ্বারা গুণ কর ।
সমাধান : আমরা জানি, (x + a)(x + b) = x² + (a + b)x + ab
(5m+8)(5m+9) = (5m)² + (8+9) x 5m+8×9
=25m² + 17 x 5m + 72
= 25m²+85m+72
উদাহরণ ১১ ।
(5a-7b)² + 2(5a7b)(9b-4a) + (9b-4a)²
সমাধান :
ধরি, (5a7b) = x এবং 9b – 4a = y
.: প্রদত্ত রাশি = x 2 + 2xy + y2
= (x + y)²
= (5a-7b+9b-4a)2 [x এবং y এর মান বসিয়ে ]
= (a + 2b)2
= a²+4ab + 462

উদাহরণ ১২।
(x + 6) (x + 4) কে দুইটি রাশির বর্গের অন্তররূপে প্রকাশ কর ।
সমাধান : আমরা জানি, ab = {(a+b)/2}² – {(a-b)/2}²
(x + 6) (x + 4) = {(x+6+x+4)/2}2 – {(x+6-x-4)/2}2
= {(2x+10)/2} ² – (2/2)2
= (x+5)²-1²
উদাহরণ ১৩।
x=4, y = −8 এবং z = 5 হলে, 25(x + y)² − 20(x + y)(y + z) + 4(y + z)² এর মান কত ?
সমাধান :
ধরি, x + y = a এবং y + z = b
প্রদত্ত রাশি =25a²-20ab + 4b2
= (5a)2-2 × 5a × 2b + (2b)²
= (5a – 2b)²
= {5(x+y)-2(y + z)}2 [a ও b এর মান বসিয়ে ]
=(5x+5y-2y-2z)2
=(5x + 3y-2z)2
= {5×4+3x(-8)-2×5}2 [x, y ও z এর মান বসিয়ে ]
= (20-24-10)2
= (-14)² = 196
(a + b + c) 2 এর জ্যামিতিক ব্যাখ্যা :
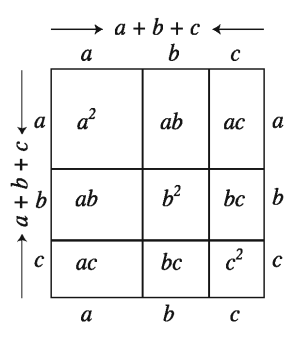
সম্পূর্ণ বর্গক্ষেত্রটির ক্ষেত্রফল
(a+b+c)x(a+b+c)=(a+b+c)²
(a+b+c)²=a x (a+b+c) + b x (a+b+c)+c x (a+b+c)
= a² + ab + ac + ab + b² + bc + ca + bc + c²
= a²+2ab+2ac + b²+2bc + c²
(a+b+c)²= a² + b² + c²+2ab+2bc+2ac
আবার, বর্গক্ষেত্রটির অংশগুলোর ক্ষেত্রফলের সমষ্টি
= a² + ab + ac + ab + b² + bc + ac + bc + c²
=a2+2ab+2ac + b²+2bc + c²
= a² + b² + c²+2ab+2bc + 2ac
লক্ষ করি, সম্পূর্ণ বর্গক্ষেত্রটির ক্ষেত্রফল = বর্গক্ষেত্রটির অংশগুলোর ক্ষেত্রফলের সমষ্টি
:. (a + b + c)² = a² + b² + c²+2ab+2bc + 2ac
উদাহরণ ১৪ ।
2x + 3y + 5z এর বর্গ নির্ণয় কর ।
সমাধান :
ধরি, 2x = a, 3y = b এবং 5z = c
প্রদত্ত রাশির বর্গ = (a+b+c)²
= a² + b² + c²+2ab+2bc+2ac
=(2x)²+(3y)²+(5z)²+2×2x × 3y+2×3yx5z+2× 2x × 5z [a,b ও c এর মান বসিয়ে ]
=4x²+9y²+252² + 12xy + 30yz + 20xz
(4x+3y+5z)² = 4x²+9y²+ 25z² + 12xy + 30yz + 20xz
উদাহরণ ১৫।
5a – 6b – 7c এর বর্গ নির্ণয় কর ।
(5α-6b-7c)² = {5a – (6b+7c)}2
= (5a)² – 2 x 5a × (6b+7c) + (6b+7c)²
= 25a² – 10a (6b+7c) + (6b)² + 2 x 6b x 7c+ (7c)2
=25a2-60ab70ac +36b2+ 84bc + 49c²
=25a² + 36b² + 49c²- 60ab + 84bc – 70ac
বিকল্প সমাধান :
আমরা জানি, (x + y + z)² = x² + y² + z² + 2xy +2yz + 2xz
এখানে, 5a = x, – 6b = y এবং – 7c = 2 ধরে
(5a-6b-7c)² = (5a)² + (−6b)² + (-7c)² + 2x (5a) x (-6b) + 2 × (−6b) × (−7c)+2 × (5a) × (-7c)
=25a²+36b2+49c2-60ab + 84bc – 70ac
