আজকে আমাদের আলোচনার বিষয়ঃ বীজগণিতীয় সূত্রাবলি ও প্রয়োগ (দ্বিপদী ও ত্রিপদী রাশির বর্গ) । এটি সপ্তম শ্রেনী গণিতের অজানা রাশির সূচক, গুণ ও তাদের প্রয়োগ এর অন্তর্গত।

বীজগণিতীয় সূত্রাবলি ও প্রয়োগ (দ্বিপদী ও ত্রিপদী রাশির বর্গ)
দ্বিপদী রাশির বর্গ
তোমাকে যদি প্রশ্ন করা হয় দুইকে দুই দিয়ে গুণ করলে কত হয়? তুমি নিশ্চয়ই উত্তরে বলবে চার হয়, তিনকে তিন দিয়ে গুণ করলে কত হয়? তুমি নিশ্চয়ই উত্তরে বলবে নয় হয়, কারণ ইতিমধ্যেই পূর্ববর্তী ক্লাসে তুমি তা জেনে এসেছ। কিন্তু যদি বলা হয় কোন একটি আয়তক্ষেত্রের দৈর্ঘ্য 2 সে.মি. ও প্রস্থ 2 সে.মি. হলে এর ক্ষেত্রফল কত? তুমি এবার নিশ্চয়ই এমন একটি আয়তক্ষেত্র অঙ্কন করবে যার দৈর্ঘ্য 2 সে.মি. ও প্রস্থ 2 সে.মি.এবং তোমার অংকিত চিত্রটি হবে নিম্নরুপ
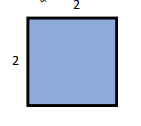
এবার যদি দৈর্ঘ্য 3 সে.মি. ও প্রস্থ 3 সে.মি.হয় তখন ক্ষেত্রফল কত হবে, যদি দৈর্ঘ্য 5 সে.মি. ও প্রস্থ 5 সে.মি.হয় তখন ক্ষেত্রফল কত হবে, যদি দৈর্ঘ্য (a + b) সে.মি. ও প্রস্থ (a + b) সে.মি.হয় তখন ক্ষেত্রফল কত হবে? চল, নিচের চিত্রগুলি লক্ষ করি।
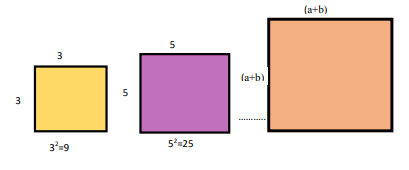
এবার চল আমরা (a + b)2 এর মান কত হবে তা বের করার চেষ্টা করি। প্রথমে বর্গাকৃতি একটি কাগজ নাও। উহা হতে নিচের চিত্রের মতো aও b বাহু চিহ্নিত কর, ফলে চারটি ক্ষেত্র চিহ্নিত হবে।
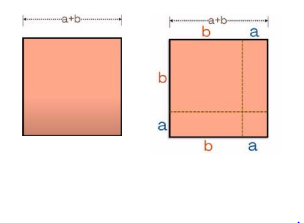
ক্ষেত্রগুলো কেটে কেটে আলাদা করো। নিচের চিত্রের মতো চারটি ক্ষেত্রফল পাওয়া যাবে।
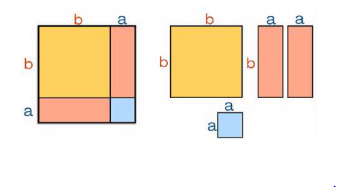
এবার আলাদা করা ক্ষেত্র গুলোকে সাজালে নিচের চিত্রের মতো ফলাফল পাওয়া যাবে।
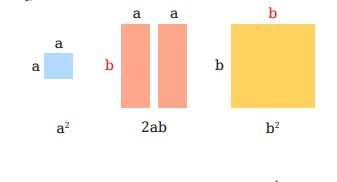
পরিশেষে আমরা নিচের চিত্র থেকে পাবো,
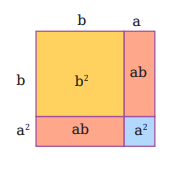
চল, এবার সূত্রটি সত্যতা যাচাই করি। এ ক্ষেত্রে আমরা জ্যামিতিক পদ্ধতি অবলম্বন করব।
ধরি, a = 3 এবং b = 2
(a + b) 2 = a 2 + 2ab + b2
এখন একটি বর্গ অঙ্কন কর যার এক বাহুর দৈর্ঘ্য (a + b)অর্থাৎ (3 + 2)
সম্পূর্ন বর্গক্ষেত্রের ক্ষেত্রফল হবে ( 3 + 2)2 = 52 = 25
3 একক বাহু বিশিষ্ট বর্গের ক্ষেত্রফল= 9 বর্গ একক
2 একক বাহু বিশিষ্ট বর্গের ক্ষেত্রফল= 4 বর্গ একক
3 একক এবং 2 একক বাহু বিশিষ্ট আয়তক্ষেত্রের ক্ষেত্রফল= 6 বর্গএকক
2 একক এবং 3 একক বাহু বিশিষ্ট আয়তক্ষেত্রের ক্ষেত্রফল= 6 বর্গএকক
এ ক্ষেত্রেও সম্পূর্ন বর্গক্ষেত্রের ক্ষেত্রফল হবে= (9+4+6+6) বর্গ একক 25 বর্গ একক
যেহেতু, উভয় ক্ষেত্রেই ক্ষেত্রফলের মান সমান। কাজেই বলা যায়, (a + b) 2 = a 2 + 2ab + b2
