ত্রিভুজ ও বৃত্ত বিষয়ক উপপাদ্য

আজকে আমরা  ত্রিভুজ ও বৃত্ত বিষয়ক উপপাদ্য সম্পর্কে  আলোচনা করবো । যা উচ্চতর গণিতের জ্যামিতি অংশের অন্তর্গত।

 

 

ত্রিভুজ ও বৃত্ত বিষয়ক উপপাদ্য

এই অংশে ত্রিভুজ ও বৃত্ত বিষয়ক কয়েকটি গুরুত্বপূর্ণ উপপাদ্যের যুক্তিমূলক প্রমাণ উপস্থাপন করা হবে। উপপাদ্যসমূহ প্রমাণের জন্য দুইটি ত্রিভুজের সদৃশতা সম্পর্কে পূর্বজ্ঞান থাকা আবশ্যক। মাধ্যমিক জ্যামিতিতে ত্রিভুজের সদৃশতা সম্পর্কে বিস্তারিত আলোচনা করা হয়েছে। শিক্ষার্থীদের সুবিধার্থে ত্রিভুজের সদৃশতা সম্পর্কে সংক্ষেপে আলোচনা করা হলো।

কোণের ক্ষেত্রে সদৃশতা:

সমান সংখ্যক বাহুবিশিষ্ট দুইটি বহুভুজের একটির কোণগুলো যদি যথাক্রমে অপরটির কোণগুলোর সমান হয়, তবে বহুভুজ দুইটিকে সদৃশকোণী বহুভুজ বলা হয় ।

বাহুর অনুপাতের ক্ষেত্রে সদৃশতা সমান সংখ্যক বাহুবিশিষ্ট দুইটি বহুভুজের একটির শীর্ষ বিন্দুগুলোকে যদি যথাক্রমে অপরটির শীর্ষবিন্দুগুলোর সঙ্গে এমনভাবে মিল করা যায় যে, বহুভুজ দুইটির

ক) অনুরূপ কোণগুলো সমান হয় এবং

খ) অনুরূপ দুইটি বাহুর অনুপাত সমান হয়

তবে বহুভুজ দুইটিকে সদৃশ (similar) বহুভুজ বলা হয়।

 

 

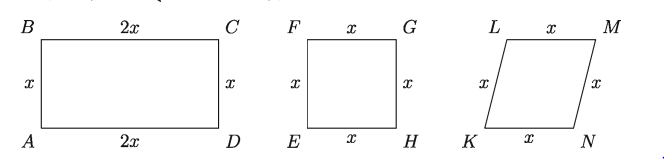
উপরের চিত্রে লক্ষ করলে দেখব যে,

ক) আয়ত ABCD ও বর্গ EFGH সদৃশ নয় যদিও তারা সদৃশকোণী। সবগুলো কোণই সমকোণ কিন্তু অনুরূপ বাহুগুলোর অনুপাত সমান নয়।

খ) বর্গ EFGH ও রম্বস KLMN সদৃশ নয় যদিও তাদের শীর্ষবিন্দুগুলোর যেকোনো ধারাবাহিক মিলকরণের ফলে অনুরূপ বাহু দুইটির অনুপাতগুলো সমান কিন্তু অনুরূপ কোণগুলো সমান নয়।

দুইটি ত্রিভুজের বেলায় অবশ্য এ রকম হয় না। দুইটি ত্রিভুজের শীর্ষবিন্দুগুলোর কোণ মিলকরণের ফলে যদি সদৃশতার সংজ্ঞায় উল্লেখিত শর্ত দুইটির একটি সত্য হয়, তবে অপরটিও সত্য হয় এবং ত্রিভুজ দুইটি সদৃশ হয়। এ প্রসঙ্গে উল্লেখ্য যে,

ক) দুইটি ত্রিভুজ সদৃশকোণী হলে সমান কোণ দুইটিকে অনুরূপ কোণ এবং অনুরূপ কোণের বিপরীত বাহু দুইটিকে অনুরূপ বাহু ধরা হয়।

খ) দুইটি ত্রিভুজের একটির দুই বাহু অপরটির দুই বাহুর সমানুপাতিক হলে, আনুপাতিক বাহু দুইটিকে অনুরূপ বাহু এবং অনুরূপ বাহুর বিপরীত কোণ দুইটিকে অনুরূপ কোণ ধরা হয়।

গ) উভয়ক্ষেত্রে অনুরূপ কোণগুলোর শীর্ষবিন্দু মিল করে ত্রিভুজ দুইটি বর্ণনা করা হয়। যেমন, AABC ও ADEF এর অনুরূপ কোণগুলো হচ্ছে ZA ও ZD, LB ও ZE, LC ও ZF এবং অনুরূপ বাহুগুলো হচ্ছে AB ও DE, AC ও DF, BC ও EF |

দুইটি ত্রিভুজের সদৃশতা সম্পর্কিত কয়েকটি উপপাদ্যের সংক্ষিপ্ত বর্ণনা দেওয়া হলো।

উপপাদ্য ৬.

দুইটি ত্রিভুজ সদৃশকোণী হলে তাদের অনুরূপ বাহুগুলো সমানুপাতিক হবে ।

 

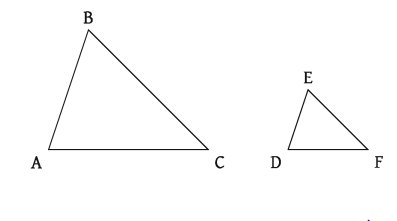
উপরের চিত্রে AABC ও ADEF সদৃশকোণী ত্রিভুজ।

অর্থাৎ, ZA = ZD, LB = LE এবং LC = ZF হওয়ায় AB DE AC DF BC EF = = হবে।

অর্থাৎ অনুরূপ বাহুগুলো সমানুপাতিক হবে।

অনুসিদ্ধান্ত ১.

দুইটি ত্রিভুজ সদৃশকোণী হলে, তারা সদৃশ হয়।

মন্তব্য:

দুইটি ত্রিভুজের একটির দুই কোণ অপরটির দুই কোণের সমান হলে ত্রিভুজ দুইটি সদৃশকোণী এবং এর ফলে এগুলো সদৃশ হয়। কারণ যেকোনো ত্রিভুজের তিন কোণের সমষ্টি দুই সমকোণ।

উপপাদ্য ৭.

দুইটি ত্রিভুজের বাহুগুলো পরস্পরের সমানুপাতিক হলে অনুরূপ বাহুগুলোর বিপরীত কোণগুলো পরস্পর সমান হয়।

 

 

 

উপরের চিত্রে AABC ও ADEF এর বাহুগুলো সমানুপাতিক অর্থাৎ AB AC BC = = DE DF EF ত্রিভুজদ্বয়ের কোণগুলো পরস্পর সমান। সুতরাং, ZA = ZD, LB = ZE এবং ZC = ZF হওয়ায় উপপাদ্য ৬ কে উপপাদ্য ৭ এর বিপরীত উপপাদ্য বলা যেতে পারে।

উপপাদ্য ৮.

দুইটি ত্রিভুজের একটির এক কোণ অপরটির এক কোণের সমান এবং সমান কোণ সংলগ্ন বাহুগুলো সমানুপাতিক হলে ত্রিভুজ দুইটি সদৃশ হবে।

নিচের চিত্রের AABC ও DEF এর ZA ZD এবং সমান কোণ সংলগ্ন বাহুদ্বয় AB, AC = AB AC = DE DF এবং DE, DF সমানুপাতিক। অর্থাৎ হওয়ায় AABC ও ADEF সদৃশ।

 

উপপাদ্য ৯.

দুইটি সদৃশ ত্রিভুজক্ষেত্রের ক্ষেত্রফলদ্বয়ের অনুপাত তাদের যেকোনো দুই অনুরূপ বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলদ্বয়ের অনুপাতের সমান।

নিচের চিত্রের AABC ও DEF ত্রিভুজদ্বয় সদৃশ। ত্রিভুজ দুইটির অনুরূপ বাহু BC ও EF | এই অবস্থায় ত্রিভুজদ্বয়ের ক্ষেত্রফলের অনুপাত BC ও EF বাহুদ্বয়ের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলদ্বয়ের অনুপাতের সমান। অর্থাৎ, DE এবং AC ও DF অনুরূপ হলে, ABC BC2 ADEF = EF2 ABC AB2 = ADEF DE2 = ।

 

 

ত্রিভুজের পরিকেন্দ্র, ভরকেন্দ্র ও লম্ববিন্দু

এখানে উল্লেখ্য, কোনো ত্রিভুজের লম্ববিন্দু থেকে শীর্ষের দূরত্ব ত্রিভুজের পরিকেন্দ্র থেকে ঐ শীর্ষের বিপরীত বাহুর লম্ব দূরত্বের দ্বিগুণ।

ত্রিভুজের পরিকেন্দ্র :

ত্রিভুজের যেকোনো দুই বাহুর লম্বদ্বিখণ্ডক যে বিন্দুতে ছেদ করে তাকে ত্রিভুজের পরিকেন্দ্র বলে। উল্লেখ্য, তৃতীয় বাহুর লম্বদ্বিখণ্ডকও ঐ বিন্দুগামী।

ত্রিভুজের ভরকেন্দ্র:

ত্রিভুজের মধ্যমাগুলো যে বিন্দুতে ছেদ করে ঐ বিন্দুকে ত্রিভুজটির ভরকেন্দ্র বলা  হয়। ত্রিভুজের ভরকেন্দ্রে মধ্যমাগুলো 2 : 1 অনুপাতে বিভক্ত হয়।

ত্রিভুজের লম্ববিন্দু :

ত্রিভুজের শীর্ষবিন্দুগুলো হতে বিপরীত বাহুর উপর অঙ্কিত লম্বগুলো যে বিন্দুতে ছেদ করে তাহাই লম্ববিন্দু।

উপপাদ্য ১০.

ত্রিভুজের পরিকেন্দ্র, ভরকেন্দ্র ও লম্ববিন্দু সমরেখ

বিশেষ নির্বচন:

মনে করি, AABC এর লম্ববিন্দু O, পরিকেন্দ্র S এবং AP একটি মধ্যমা। লম্ববিন্দু O এবং পরিকেন্দ্র S এর সংযোগ রেখা AP মধ্যমাকে G বিন্দুতে ছেদ করেছে। S, P যোগ করলে SP রেখা BC এর উপর লম্ব। তাহলে, G বিন্দুটি AABC এর ভরকেন্দ্র এটি প্রমাণ করাই যথেষ্ট।

 

 

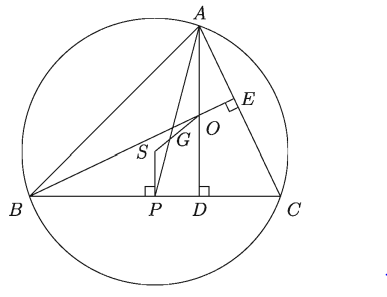
প্রমাণ:

∆ABC এর লম্ববিন্দু O থেকে A শীর্ষের দূরত্ব OA এবং পরিকেন্দ্র S থেকে A শীর্ষের বিপরীত বাহু BC এর দূরত্ব SP : OA = 2SP… · (1)

এখন যেহেতু AD ও SP উভয়ই BC এর উপর লম্ব সেহেতু AD || SP। এখন AD || SP এবং AP এদের ছেদক। সুতরাং একান্তর কোণ হওয়ায় ∆PAD = ∠APS, অর্থাৎ, ∠OAG – = ∠SPG

এখন ∆AGO এবং ∆PGS এর মধ্যে

∠AGO = ∠PGS   [বিপ্রতীপ কোণ]

∠OAG = ∠SPG [একান্তর কোণ]

অবশিষ্ট ∠AOG = অবশিষ্ট ∠PSG

∠AGO এবং ∠PGS সদৃশকোণী।

সুতরাং, AG /GP OA/ SP অর্থাৎ, AG/GP = 2SP /SP [(1) নং সমীকরণ হতে]

অতএব
AG /GP = 2:1

বা, AG : GP = 2:1

অর্থাৎ, G বিন্দু AP মধ্যমাকে 2 : 1 অনুপাতে বিভক্ত করেছে।

G বিন্দু ∆ABC এর ভরকেন্দ্র।   [প্রমাণিত]

দ্রষ্টব্য:

ক) নববিন্দু বৃত্ত (Nine Point Circle) : কোনো ত্রিভুজের বাহুগুলোর মধ্যবিন্দুত্রয়, শীর্ষবিন্দুগুলো থেকে বিপরীত বাহুত্রয়ের উপর অঙ্কিত লম্বত্রয়ের পাদবিন্দুত্রয় এবং শীর্ষবিন্দু ও লম্ববিন্দুর সংযোজক রেখাত্রয়ের মধ্যবিন্দুত্রয়, সর্বমোট এই নয়টি বিন্দু একই বৃত্তের উপর অবস্থান করে । এই বৃত্তকেই নববিন্দু বৃত্ত বলে।

খ) ত্রিভুজের লম্ববিন্দু ও পরিকেন্দ্র সংযোজনকারী রেখাংশের মধ্যবিন্দুই নববিন্দু বৃত্তের কেন্দ্র।

গ) নববিন্দু বৃত্তের ব্যাসার্ধ ত্রিভুজের পরিব্যাসার্ধের অর্ধেকের সমান।

উপপাদ্য ১১ (ব্রহ্মগুপ্তের উপপাদ্য)

বৃত্তে অন্তর্লিখিত কোনো চতুর্ভুজের কর্ণ দুইটি যদি পরস্পর লম্ব হয়, তবে তাদের ছেদ বিন্দু হতে কোনো বাহুর উপর অঙ্কিত লম্ব বিপরীত বাহুকে দ্বিখণ্ডিত করে।

বিশেষ নির্বচন:

বৃত্তে অন্তর্লিখিত ABCD চতুর্ভুজের কর্ণদ্বয় AC ও BD পরস্পরকে লম্বভাবে M বিন্দুতে ছেদ করে। M হতে BC বাহুর উপর ME লম্ব এবং বর্ধিত EM বিপরীত AD বাহুকে বিন্দুতে ছেদ করে। প্রমাণ করতে হবে AF = FD |

 

 

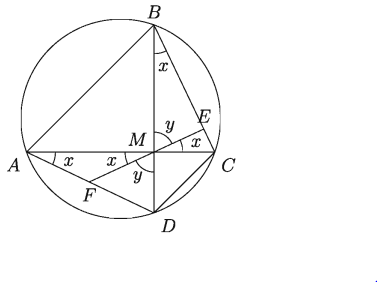
প্রমাণ:

একই চাপ CD এর উপর দন্ডায়মান বলে ∠CBD = ∠CAD

অর্থাৎ, ∠CBM = ∠MAF

আবার, ∠CBM = ∠CME [উভয়ে একই ∠BME এর পূরক কোণ বলে]

সুতরাং ∠MAF = ∠FMA

ফলে ∆AFM ত্রিভুজে AF = FM

অনুরূপভাবে দেখানো যায় যে, ∠FDM = ∠BCM = ∠BME = ∠DMF

ফলে, ∆DFM ত্রিভুজে FD = FM

সুতরাং AF = FD [প্রমাণিত]

উপপাদ্য ১২ (টলেমির উপপাদ্য)

বৃত্তে অন্তর্লিখিত কোনো চতুর্ভুজের কর্ণদ্বয়ের অন্তর্গত আয়তক্ষেত্র ঐ চতুর্ভুজের বিপরীত বাহুদ্বয়ের অন্তর্গত আয়তক্ষেত্রের সমষ্টির সমান ।

 

 

বিশেষ নির্বচন:

মনে করি বৃত্তে অন্তর্লিখিত ABCD চতুর্ভুজের বিপরীত বাহুগুলো যথাক্রমে AB ও CD এবং BC ও AD AC এবং BD চতুর্ভুজটির দুইটি কর্ণ। প্রমাণ করতে হবে যে, AC.BD =AB • CD + BC AD

প্রমাণ:

∠BAC কে ZDAC থেকে ছোট ধরে নিয়ে A বিন্দুতে AD রেখাংশের সাথে ∠BAC এর সমান করে ∠DAP আঁকি যেন AP রেখা BD কর্ণকে P বিন্দুতে ছেদ করে।

অঙ্কন অনুসারে ∠BAC = ∠DAP |

উভয়পক্ষে ∠CAP যোগ করে পাই,

∠BAC + ∠CAP : ∠DAP + ∠CAP অর্থাৎ, ∠BAP = ∠CAD = এখন ∆ABP ও ∆ACD এর মধ্যে

∠BAP = ∠CAD এবং ∠ABD = ∠ACD [একই বৃত্তাংশস্থিত কোণ সমান বলে] এবং অবশিষ্ট ∠APB = অবশিষ্ট ∠ADC

∆ABP ও ∆ACD সদৃশকোণী।

BP AB = CD AC

অর্থাৎ, AC · BP = ABCD · (1)

আবার, ∆ABC ও ∆APD এর মধ্যে

∠BAC = ∠PAD [অঙ্কন অনুসারে]

∠ADP = ∠ACB [একই বৃত্তাংশস্থিত কোণ সমান বলে]

এবং অবশিষ্ট ∠ABC = অবশিষ্ট ∠APD

∆ABC  ও ∆APD সদৃশকোণী।
AD/AC = PD/BC

AC.PD = BC. AD = ……… (2)

এখন সমীকরণ (1) ও (2) যোগ করে পাই,

AC BP + AC.PD = AB. CD + BC. AD

বা, AC(BP+PD) = AB · CD + BC. AD

কিন্তু BP+PD = BD

AC BD = AB CD + BC. AD [প্রমাণিত]

উদাহরণ ১.

∆PQR এ ∆PQR = 90° এবং PQ QR ও PR বাহু তিনটির মধ্যবিন্দু যথাক্রমে D, E ও F

ক) তথ্যানুযায়ী চিত্র এঁকে ভরকেন্দ্র চিহ্নিত কর।

খ) PR² = PE² + QE² + 2RE² |

গ) QF1 PRG 29 PA Q, QF² = PF · RF |

সমাধান :

ক) নিচের চিত্রে PQ, QR ও PR এর মধ্যবিন্দু যথাক্রমে D, E ও F হওয়ায় PE, QF এবং DR মধ্যমা। PE, QF এবং DR মধ্যমাত্রয় G বিন্দুতে ছেদ করেছে। … G বিন্দু ভরকেন্দ্র।

 

 

খ) ∆PQR = 90° এবং ∆PQR এ QR এর মধ্যবিন্দু E। P, E যোগ করি। প্রমাণ করতে হবে যে, PR 2 PE² + QE² + 2RE²

 

 

প্রমাণ:

∆PQE এ ∠PQE = 90° এবং PE অতিভুজ .. PE² = PQ² + QE² (1)

আবার,∆PQR এ ∠PQR = 90° এবং PR অতিভুজ

PR2 = PQ² + QR2

PR² = PQ² + (QE + RE)²

PR² = PQ² + QE² + RE² + 2QE · RE

PR² = PQ²+QE² + QE² + 2RE RE [QE=RE] , PR2 PE² + QE2 +2RE² [(1) ART]

PR² = PE²+QE²+2RE²

[প্রমাণিত]

গ) ∆PQR এ ∠PQR = 90° QF ⊥ PR  প্রমাণ করতে হবে যে, QF² = PF·RF

 

 

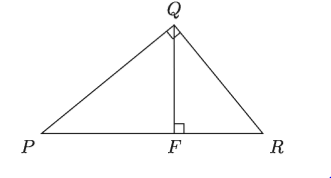
প্রমাণ:

PQR = 90°

:. ∠PQF+∠FQR = 90° ………।(1)

আবার, QF ⊥PR বলে  ∠PFQ = ∠QFR = 90°

∆PQF এ ∠PFQ + ∠PQF + ∠QPF = 180°

বা, 90° +∠PQF+∠QPF = 180°

:. ZPQF+ZQPF 90° (2)

(1) নং এবং (2) নং হতে পাই

∠PQF+∠FQR = ∠PQF + ∠QPF

∠FQR =∠QPF

∆PQF  এবং ∆QFR এ

∠PFQ=∠QFR, ∠QPF = ∠FQR

অবশিষ্ট ∠PQF = অবশিষ্ট ∠FRQ

∆PQF এবং ∆QFR সদৃশ

PQ/QF = QF/FR = PF /FQ

অর্থাৎ, QF /RF = PF /QF

বা, QF2 = PF ।RF [প্রমাণিত]

 

 

আরও দেখুনঃ

• চক্র ক্রমিক বহুপদীর উৎপাদকে বিশ্লেষণ

• ইন্টার টার্ন ফল্ট প্রোটেকশন