আজকে আমাদের আলোচনার বিষয়ঃ বৃত্ত সংক্রান্ত পরিমাপ। এটি নবম – দশম শ্রেনী গণিতের পরিমিতি অংশের অন্তর্গত।

বৃত্ত সংক্রান্ত পরিমাপ
১ . বৃত্তের পরিধি
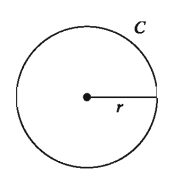
বৃত্তের দৈর্ঘ্যকে তার পরিধি বলা হয়। কোনো বৃত্তের ব্যাসার্ধ r হলে এর পরিধি c = 2πr, যেখানে π = 3.14159265… একটি অমূলদ সংখ্যা। π এর আসন্ন মান হিসেবে 3.1416 ব্যবহার করা যায়। সুতরাং কোনো বৃত্তের ব্যাসার্ধ জানা থাকলে π এর আসন্ন মান ব্যবহার করে বৃত্তের পরিধির আসন্ন মান নির্ণয় করা যায়।
উদাহরণ ১৮.
একটি বৃত্তের ব্যাস 26 সে.মি. হলে, এর পরিধি নির্ণয় কর।
সমাধান:
মনে করি, বৃত্তের ব্যাসার্ধ r
বৃত্তের ব্যাস 2r এবং পরিধি = 2πr
প্রশ্নানুসারে, 2r = 26 বা, r = 26/2 বা, r = 13 সে.মি.
বৃত্তের পরিধি = 2πr = 2 x 3.1416 x 13 সে.মি. = 81.68 সে.মি. (প্রায়)
২. বৃত্তাংশের দৈর্ঘ্য
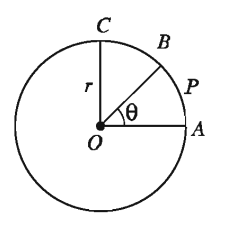
মনে করি, O কেন্দ্রবিশিষ্ট বৃত্তের ব্যাসার্ধ r এবং AB = s বৃত্তচাপ কেন্দ্রে ৪° কোণ উৎপন্ন করে।
বৃত্তের পরিধি = 2πr
বৃত্তের কেন্দ্রে মোট উৎপন্ন কোণ = 360° এবং চাপ s দ্বারা কেন্দ্রে উৎপন্ন কোণের ডিগ্রি পরিমাণ ৪°
আমরা জানি, বৃত্তের কোনো চাপ দ্বারা উৎপন্ন কেন্দ্ৰস্থ কোণ ঐ বৃত্তচাপের সমানুপাতিক ।
8/360° = s/2πr = বা, ৪ = πr8/180°

৩. বৃত্তক্ষেত্র ও বৃত্তকলা ক্ষেত্রফল
কোনো বৃত্ত দ্বারা বেষ্টিত এলাকাকে বৃত্তক্ষেত্র বলা হয় এবং বৃত্তটিকে এরূপ বৃত্তক্ষেত্রের সীমারেখা বলা হয়।
বৃত্তকলা:
একটি চাপ ও চাপের প্রান্তবিন্দু সংশ্লিষ্ট ব্যাসার্ধ দ্বারা বেষ্টিত ক্ষেত্রকে বৃত্তকলা বলা হয়।
O কেন্দ্রবিশিষ্ট বৃত্তের পরিধির উপর A ও B দুইটি বিন্দু হলে, ∠AOB এর অভ্যন্তরে OA ও OB ব্যাসার্ধ এবং AB চাপের সংযোগে গঠিত একটি বৃত্তকলা ।
পূর্বের শ্রেণীতে আমরা শিখে এসেছি যে, বৃত্তের ব্যাসার্ধ r হলে বৃত্তের ক্ষেত্রফল = πr2
আমরা জানি, বৃত্তের কোনো চাপ দ্বারা উৎপন্ন কেন্দ্রস্থ কোণ ঐ বৃত্তচাপের সমানুপাতিক ।

সুতরাং, এ পর্যায়ে আমরা স্বীকার করে নিতে পারি যে, একই বৃত্তের দুইটি বৃত্তাংশ ক্ষেত্র এবং এরা যে চাপ দুইটির উপর দন্ডায়মান এদের পরিমাপ সমানুপাতিক।
মনে করি, O কেন্দ্রবিশিষ্ট বৃত্তের ব্যাসার্ধ ।। AOB বৃত্তকলা ক্ষেত্রটি APB চাপের উপর দন্ডায়মান, যার ডিগ্রি পরিমাপ ৪। OA এর উপর OC লম্ব টানি।
বৃত্তকলা AOB এর ক্ষেত্রফল/বৃত্তকলা AOC এর ক্ষেত্রফল = ∠AOB এর পরিমাপ/∠AOC এর পরিমাপ
বা, বৃত্তকলা AOB এর ক্ষেত্রফল/ বৃত্তকলা AOC এর ক্ষেত্রফল = 8/90° [ : ∠AOC = 90°]
বা, বৃত্তকলা AOB এর ক্ষেত্রফল = 8/90° × বৃত্তকলা AOC এর ক্ষেত্রফল
= 8/90° × 1/4 × বৃত্তের ক্ষেত্রফল
8/90° × 1/4 × πr2
= 8/360° × πr2
সুতরাং বৃত্তকলার ক্ষেত্রফল = 360° × πr2
উদাহরণ ১৯.
একটি বৃত্তের ব্যাসার্ধ ৪ সে.মি. এবং একটি বৃত্তচাপ কেন্দ্রে 56° কোণ উৎপন্ন করলে, বৃত্তচাপের দৈর্ঘ্য এবং বৃত্তকলার ক্ষেত্রফল নির্ণয় কর।
সমাধান:
মনে করি, বৃত্তের ব্যাসার্ধ r = ৪ সে.মি., বৃত্তচাপের দৈর্ঘ্য s এবং বৃত্তচাপ দ্বারা কেন্দ্ৰে উৎপন্ন কোণ 8 = 56°
আমরা জানি, s = πr8/180° = (3.1416 x 8 x 56°)/180° সে.মি. = 7.82 সে.মি. (প্রায়) এবং
বৃত্তাংশের ক্ষেত্রফল 8/360 × πr2 = 56/360° x 3.1416 x 82 বর্গ সে.মি. = 31.28 বর্গ সে.মি. (প্রায়)
উদাহরণ ২০.
একটি বৃত্তের ব্যাস ও পরিধির পার্থক্য 90 সে.মি. হলে, বৃত্তের ব্যাসার্ধ নির্ণয় কর।
সমাধান:
মনে করি, বৃত্তের ব্যাসার্ধ r
বৃত্তের ব্যাস = 2r এবং পরিধি = 2πr
প্রশ্নানুসারে, 2πr – 2r = 90
বা, 2r (π – 1 ) = 90
বা, r = 90/2 (π – 1 ) = 45/(3.1416 – 1) = 21.01 সে.মি. (প্রায়)
নির্ণেয় বৃত্তের ব্যাসার্ধ 21.01 সে.মি. (প্রায়)
উদাহরণ ২১.
একটি বৃত্তাকার মাঠের ব্যাস 124 মিটার। মাঠের সীমানা ঘেঁষে 6 মিটার চওড়া একটি রাস্তা আছে। রাস্তার ক্ষেত্রফল নির্ণয় কর।

সমাধান:
মনে করি, বৃত্তাকার মাঠের ব্যাসার্ধ । এবং রাস্তাসহ বৃত্তাকার মাঠের ব্যাসার্ধ R.
r = 124/2মিটার = 62 মিটার এবং R = (62 + 6) মিটার = 68 মিটার
বৃত্তাকার মাঠের ক্ষেত্রফল = πr2 এবং রাস্তাসহ বৃত্তাকার মাঠের ক্ষেত্রফল = πR2
রাস্তার ক্ষেত্রফল = রাস্তাসহ মাঠের ক্ষেত্রফল – মাঠের ক্ষেত্রফল
= (πR2 – πr2 ) = π(R2 – r2)
= 3.1416(682 – 622) = 3.1416(4624-3844)
= 3.1416 x 780 = 2450.44 বর্গমিটার (প্রায়)
নির্ণেয় রাস্তার ক্ষেত্রফল 2450.44 বর্গমিটার (প্রায়)
উদাহরণ ২২.
একটি বৃত্তের ব্যাসার্ধ 12 সে.মি. এবং বৃত্তচাপের দৈর্ঘ্য 14 সে.মি.। বৃত্তচাপটি কেন্দ্রে যে কোণ উৎপন্ন করে তা নির্ণয় কর।
সমাধান:
মনে করি, বৃত্তের ব্যাসার্ধ r = 12 সে.মি., বৃত্তচাপের দৈর্ঘ্য ৪ = 14 সে.মি. এবং কেন্দ্ৰে উৎপন্ন কোণের ডিগ্রি পরিমাণ ৪
আমরা জানি, s = πrθ/180
বা, πrθ = 180 x 8
বা, θ = (180 x s)/πr = (180 x 14) /(3.1416 x 12) = 66.84° (প্রায়)
নির্ণেয় কোণ 66.84° (প্রায়)
উদাহরণ ২৩.
একটি চাকার ব্যাস 4.5 মিটার। চাকাটি 360 মিটার পথ অতিক্রম করতে কত বার ঘুরবে?
সমাধান:
দেওয়া আছে, চাকার ব্যাস 4.5 মিটার।
চাকাটির ব্যাসার্ধ r = 2.25 মিটার এবং পরিধি = 2πr
মনে করি, চাকাটি 360 মিটার পথ অতিক্রম করতে n বার ঘুরবে।
প্রশ্নানুসারে, n x 2πr = 360
বা, n = 360/2πr = 360 /(2 x 3.1416 x 2.25) = 25.46 (প্রায়)
চাকাটি প্রায় 25 বার ঘুরবে।
উদাহরণ ২৪.
211 মিটার 20 সে.মি. যেতে দুইটি চাকা যথাক্রমে 32 এবং 48 বার ঘুরলো। চাকা দুইটির ব্যাসার্ধের অন্তর নির্ণয় কর।
সমাধান:
211 মিটার 20 সে.মি. = 21120 সে.মি.
মনে করি, চাকা দুইটির ব্যাসার্ধ যথাক্রমে R ও r যেখানে R>r
চাকা দুইটির পরিধি যথাক্রমে 2πR ও 2πr এবং ব্যাসার্ধের অন্তর (R – r)
প্রশ্নানুসারে, 32 x 2πR = 21120
বা R = 21120/(32 x 2π) = 21120/(32 x 2 x 3.1416) = 105.04 সে.মি. (প্রায়)
এবং 48 x 2πr = 21120
বা, r = 21120/(48 × 2π) = 21120/(48 x 2 × 3.1416) = 70.03 সে.মি. (প্রায়) .
R – r = (105.04 – 70.03 ) = 35.01 সে.মি. = 0.35 মি (প্রায়)
চাকা দুইটির ব্যাসার্ধের অন্তর 0.35 মিটার (প্রায়)
উদাহরণ ২৫.
একটি বৃত্তের ব্যাসার্ধ 14 সে.মি.। একটি বর্গের ক্ষেত্রফল উক্ত বৃত্তের ক্ষেত্রফলের সমান । বর্গক্ষেত্রটির বাহুর দৈর্ঘ্য নির্ণয় কর।
সমাধান:
মনে করি, বৃত্তের ব্যাসার্ধ r = 14 সে.মি. এবং বর্গক্ষেত্রটির বাহুর দৈর্ঘ্য a
বৃত্তের ক্ষেত্রফল πr2 এবং বর্গক্ষেত্রটির ক্ষেত্রফল = a2
প্রশ্নানুসারে, a2 = πr2
বা, a = √πr = √3.1416 x 14 = 24.81 (প্রায়)
নির্ণেয় দৈর্ঘ্য 24.81 সে.মি. (প্রায়)
উদাহরণ ২৬
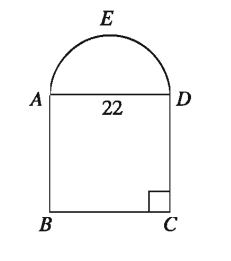
চিত্রে ABCD একটি বর্গক্ষেত্র যার প্রতি বাহুর দৈর্ঘ্য 22 মিটার এবং AED ক্ষেত্রটি একটি অর্ধবৃত্ত। সম্পূর্ণ ক্ষেত্রটির ক্ষেত্রফল নির্ণয় কর।
সমাধান:
মনে করি, ABCD বর্গক্ষেত্রটির প্রতিবাহুর দৈর্ঘ্য a.
সুতরাং, ABCD বর্গক্ষেত্রের ক্ষেত্রফল = a2
আবার, AED একটি অধিবৃত্ত
অর্ধবৃত্তের ব্যাসার্ধ r =22/2 মিটার = 11 মিটার
সুতরাং, AED অর্ধবৃত্তের ক্ষেত্রফল = 1/2πr2
.:. সম্পূর্ণ ক্ষেত্রের ক্ষেত্রফল = ABCD বর্গক্ষেত্রের ক্ষেত্রফল + AED অর্ধবৃত্তের ক্ষেত্রফল
= (a² + 1/2πr²)
= (222 + 1/2 × 3.1416 × 112 ) = 674.07 বর্গমিটার (প্রায়)
নির্ণেয় ক্ষেত্রফল 674.07 বর্গমিটার (প্রায়)
উদাহরণ ২৭.
চিত্রে ABCD একটি আয়তক্ষেত্র যার দৈর্ঘ্য ও প্রস্থ যথাক্রমে 12 মিটার ও 10 মিটার এবং DAE একটি বৃত্তাংশ। বৃত্তচাপ DE এর দৈর্ঘ্য এবং সম্পূর্ণ ক্ষেত্রের ক্ষেত্রফল নির্ণয় কর।

সমাধান:
বৃত্তাংশের ব্যাসার্ধ r = AD = 12 মিটার এবং কেন্দ্রে উৎপন্ন কোণ ৪ = 30°
বৃত্তচাপ DE এর দৈর্ঘ্য = πεθ/180
= (3.1416 x 12 x 30)/ 180 = 6.28 মিটার (প্রায়)
ADE বৃত্তাংশের ক্ষেত্রফল = θ/360 × πr2
= 30/360 x 3.1416 x 122
= 37.7 বর্গমিটার (প্রায়)
আয়তক্ষেত্র ABCD এর দৈর্ঘ্য 12 মিটার এবং প্রস্থ 10 মিটার
আয়তক্ষেত্রটির ক্ষেত্রফল = দৈর্ঘ্য x প্রস্থ = 12 × 10 = 120 বর্গমিটার
সম্পূর্ণ ক্ষেত্রের ক্ষেত্রফল = ( 37.7 +120) বর্গমিটার = 157.7 বর্গমিটার (প্রায়)
নির্ণেয় ক্ষেত্রফল 157.7 বর্গমিটার (প্রায়)।