আজকে আমাদের আলোচনার বিষয়ঃ বৃত্ত সম্পর্কিত উপপাদ্য । এটি অষ্টম শ্রেনী গণিতের বৃত্তের অন্তর্গত।

বৃত্ত সম্পর্কিত উপপাদ্য
উপপাদ্য ১ ।
বৃত্তের কেন্দ্র ও ব্যাস ভিন্ন কোনো জ্যা-এর মধ্যবিন্দুর সংযোজক রেখাংশ ঐ জ্যা-এর উপর লম্ব ।
মনে করি, O কেন্দ্রবিশিষ্ট বৃত্তে AB ব্যাস নয় এমন একটি জ্যা এবং M এই জ্যা-এর মধ্যবিন্দু । O M যোগ করি ।
প্রমাণ করতে হবে যে, OM রেখাংশ AB জ্যা-এর উপর লম্ব।
অঙ্কন :
O, A এবং O, B যোগ করি ।
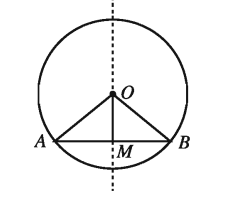
প্ৰমাণ :
|
ধাপ |
যথার্থতা |
| (১) ∆DAM এবং ∆OBM এ
AM = BM OA = OB এবং OM = OM সুতরাং ∆OAM ≌ ∆OBM ∠OMA = ∠OMB (২) যেহেতু কোণদ্বয় রৈখিক যুগল কোণ এবং এদের পরিমাপ সমান, সুতরাং, ∠OMA = ∠OMB = ১ সমকোণ । অতএব, OM ⊥AB (প্রমাণিত) |
[M,AB এর মধ্যবিন্দু ]
[ উভয়ে একই বৃত্তের ব্যাসার্ধ ] [ সাধারণ বাহু ] [ বাহু-বাহু-বাহু উপপাদ্য ] |
অনুসিদ্ধান্ত ১।
বৃত্তের যেকোনো জ্যা-এর লম্বসম-দ্বিখণ্ডক কেন্দ্রগামী ।
অনুসিদ্ধান্ত ২।
যেকোনো সরলরেখা একটি বৃত্তকে দুইয়ের অধিক বিন্দুতে ছেদ করতে পারে না ।
অনুশীলনী
১। প্রামণ কর যে, কোনো বৃত্তের দুইটি জ্যা পরস্পরকে সমদ্বিখণ্ডিত করলে তাদের ছেদবিন্দু বৃত্তটির কেন্দ্র হবে ।
২ । প্রমাণ কর যে, দুইটি সমান্তরাল জ্যা-এর মধ্যবিন্দুর সংযোজক সরলরেখা কেন্দ্রগামী এবং জ্যাদ্বয়ের উপর লম্ব ।
৩। কোনো বৃত্তের AB ও AC জ্যা দুইটি A বিন্দুগামী ব্যাসার্ধের সাথে সমান কোণ উৎপন্ন করে । প্রমাণ কর যে, AB = AC
৪ । চিত্রে, O বৃত্তের কেন্দ্র এবং জ্যা AB = জ্যা AC । প্রমাণ কর যে, ∠BAO = ∠CAO
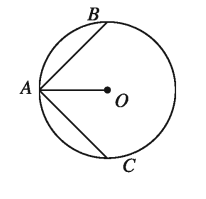
৫। কোনো বৃত্ত একটি সমকোণী ত্রিভুজের শীর্ষবিন্দুগুলো দিয়ে যায়। দেখাও যে, বৃত্তটির কেন্দ্র অতিভুজের মধ্যবিন্দু ।
৬। দুইটি সমকেন্দ্রিক বৃত্তের একটির AB জ্যা অপর বৃত্তকে C ও D বিন্দুতে ছেদ করে । প্রমাণ কর যে, AC = BD
উপপাদ্য ২ ।
বৃত্তের সকল সমান জ্যা কেন্দ্র থেকে সমদূরবর্তী।
মনে করি, O বৃত্তের কেন্দ্র এবং AB ও CD বৃত্তের দুইটি সমান জ্যা । প্রমাণ করতে হবে যে, O থেকে AB এবং CD জ্যাদ্বয় সমদূরবর্তী।
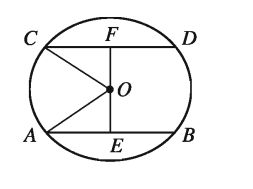
অঙ্কন :
O থেকে AB এবং CD জ্যা-এর উপর যথাক্রমে OE এবং OF লম্ব রেখাংশ আঁকি । O, A এবং O,C যোগ করি ।
প্ৰমাণ :
|
ধাপ |
যথার্থতা |
| (১) OE ⊥ AB
ও OF ⊥CD সুতরাং, AE = BE এবং CF = DF AE = 1/2AB এবং CF = 1/2CD (২) কিন্তু, AB = CD বা 1/2AB = 1/2CD AE = CF (৩) এখন ∆DAE এবং ∆OCF সমকোণী ত্রিভুজদ্বয়ের মধ্যে অতিভুজ OA = অতিভুজ OC এবং AE = CF ∆OAE = ∆OCF OE = OF (৪) কিন্তু OF এবং OF কেন্দ্র O থেকে যথাক্রমে AB জ্যা এবং CD জ্যা এর দূরত্ব। সুতরাং, AB এবং CD জ্যাদ্বয় বৃত্তের কেন্দ্র থেকে | সমদূরবর্তী । (প্রমাণিত) |
[ কেন্দ্র থেকে ব্যাস ভিন্ন যেকোনো জ্যা-এর উপর অঙ্কিত লম্ব জ্যাকে সমদ্বিখণ্ডিত করে ]
[ কল্পনা ] [ উভয়ে একই বৃত্তের ব্যাসার্ধ ] [ ধাপ ২ ] [ সমকোণী ত্রিভুজের অতিভুজ-বাহু সমসমতা উপপাদ্য] |
উপপাদ্য ৩
বৃত্তের কেন্দ্র থেকে সমদূরবর্তী সকল জ্যা পরস্পর সমান ।
মনে করি, O বৃত্তের কেন্দ্র এবং AB ও CD দুইটি জ্যা। ০ থেকে AB ও CD এর উপর যথাক্রমে OE ও OF লম্ব। তাহলে OE 3 OF কেন্দ্র থেকে যথাক্রমে AB ও CD জ্যা এর দূরত্ব নির্দেশ করে । OE = OF হলে প্রমাণ করতে হবে যে, AB = CD

অঙ্কন :
O, A এবং O, C যোগ করি ।
প্ৰমাণ :
|
ধাপ |
যথার্থতা |
| (১) যেহেতু OE ⊥ AB এবং OF ⊥ CD. সুতরাং,
∠OEA = ∠OFC = এক সমকোণ (২) এখন, ∆OAE এবং ∆OCF সমকোণী ত্রিভুজদ্বয়ের মধ্যে অতিভুজ OA = অতিভুজ OC এবং OE = OF ∆OAE ≌ ∆OCF AE = CF (৩) AE = 1/2 AB এবং CF = 1/2CD (৪) সুতরাং 1/2 AB = 1/2CD অর্থাৎ. AB = CD |
[ সমকোণ ]
[উভয়ে একই বৃত্তের ব্যাসার্ধ ] [কল্পনা ] [সমকোণী ত্রিভুজের অতিভুজ-বাহু সর্বসমতা উপপাদ্য] [ কেন্দ্র থেকে ব্যাস ভিন্ন যেকোনো জ্যা-এর উপর অঙ্কিত লম্ব জ্যাকে সমদ্বিখণ্ডিত করে ] |
উদাহরণ ৪।
প্রমাণ কর যে, বৃত্তের ব্যাসই বৃহত্তম জ্যা। মনে করি, O কেন্দ্রবিশিষ্ট ABDC একটি বৃত্ত। AB ব্যাস এবং CD ব্যাস ভিন্ন যেকোনো একটি জ্যা ।
প্রমাণ করতে হবে যে, AB > CD
অঙ্কন :
O, C এবং O, D যোগ করি ।
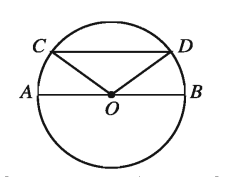
প্রমাণঃ
OA = OB = OC = OD [একই বৃত্তের ব্যাসার্ধ ]
এখন, ∆OCD এ
OC+ OD > CD
বা, OA+ OB > CD
অর্থাৎ, AB > CD
[ : ত্রিভুজের যে কোনো দুই বাহুর সমষ্টি তৃতীয় বাহু অপেক্ষা বৃহত্তর]
অনুশীলনী
১। বৃত্তের দুইটি সমান জ্যা পরস্পরকে ছেদ করলে দেখাও যে, এদের একটির অংশদ্বয় অপরটির অংশদ্বয়ের সমান ।
২। প্রমাণ কর যে, বৃত্তের সমান জ্যা-এর মধ্যবিন্দুগুলো সমবৃত্ত ।
৩। দেখাও যে, ব্যাসের দুই প্রান্ত থেকে এর বিপরীত দিকে দুইটি সমান জ্যা অঙ্কন করলে এরা সমান্তরাল হয়।
8। দেখাও যে, ব্যাসের দুই প্রান্ত থেকে এর বিপরীত দিকে দুইটি সমান্তরাল জ্যা আঁকলে এরা সমান হয় ।
৫। দেখাও যে, বৃত্তের দুইটি জ্যা-এর মধ্যে বৃহত্তর জ্যা-টি ক্ষুদ্রতর জ্যা অপেক্ষা কেন্দ্রের নিকটতর ।
৬। O কেন্দ্র বিশিষ্ট বৃত্তে PQ এবং RS দু’টি সমান জ্যা এর মধ্যবিন্দু যথাক্রমে M ও N।
ক) 314 বর্গ সে.মি. ক্ষেত্রফলবিশিষ্ট বৃত্তের ব্যাসার্ধ নির্ণয় কর।
খ) প্রমাণ কর যে, OM=ON
গ) PQ এবং RS জ্যাদ্বয় বৃত্তের অভ্যন্তরে পরস্পরকে ছেদ করলে প্রমাণ কর যে, একটির অংশদ্বয় অপরটির অংশদ্বয়ের সমান ।
