বৃত্ত সম্পৰ্কীয় সম্পাদ্য

আজকে আমাদের আলোচনার বিষয়ঃ বৃত্ত সম্পৰ্কীয় সম্পাদ্য ।  এটি নবম – দশম শ্রেনী গণিতের বৃত্ত এর অন্তর্গত।

 

 

বৃত্ত সম্পৰ্কীয় সম্পাদ্য

সম্পাদ্য ৬

একটি বৃত্ত বা বৃত্তচাপ দেওয়া আছে, কেন্দ্র নির্ণয় করতে হবে।

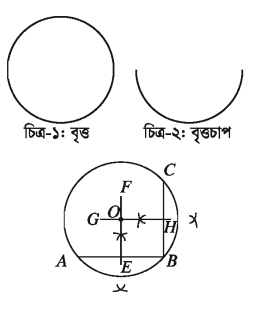
একটি বৃত্ত (চিত্র-১) বা বৃত্তচাপ (চিত্র-২) দেওয়া আছে, বৃত্তটির বা বৃত্তচাপটির কেন্দ্র নির্ণয় করতে হবে।

অঙ্কন:

প্রদত্ত বৃত্ত বা বৃত্তচাপে তিনটি বিন্দু A, B ও C নিই। A, B ও B, C যোগ করি। AB ও BC জ্যা দুইটির লম্বদ্বিখণ্ডক। যথাক্রমে EF, GH রেখাংশ দুইটি টানি। মনে করি, তারা পরস্পর O বিন্দুতে ছেদ করে। সুতরাং, O বিন্দুই বৃত্ত বা বৃত্তচাপের কেন্দ্র। প্রমাণ: EF রেখাংশ AB জ্যা এর এবং GH রেখাংশ BC জ্যা এর লম্বদ্বিখণ্ডক। কিন্তু EF ও GH উভয়ে কেন্দ্রগামী এবং O এদের সাধারণ ছেদ বিন্দু। সুতরাং O বিন্দুই বৃত্ত বা বৃত্তচাপের কেন্দ্ৰ।

 

 

বৃত্তের স্পর্শক অঙ্কন

আমরা জেনেছি যে, বৃত্তের ভিতরে অবস্থিত কোনো বিন্দু থেকে বৃত্তের স্পর্শক আঁকা যায় না। বিন্দুটি যদি বৃত্তের ওপর থাকে তাহলে উক্ত বিন্দুতে বৃত্তের একটিমাত্র স্পর্শক অঙ্কন করা যায়। স্পর্শকটি বর্ণিত বিন্দুতে অঙ্কিত ব্যাসার্ধের উপর লম্ব হয়। সুতরাং, বৃত্তস্থিত কোনো বিন্দুতে বৃত্তের স্পর্শক অঙ্কন করতে হলে বর্ণিত বিন্দুতে ব্যাসার্ধ অঙ্কন করে ব্যাসার্ধের উপর লম্ব আঁকতে হবে। আবার বিন্দুটি বৃত্তের বাইরে অবস্থিত হলে তা থেকে বৃত্তে দুইটি স্পর্শক আঁকা যাবে।

সম্পাদ্য ৭.

বৃত্তের কোনো বিন্দুতে একটি স্পর্শক আঁকতে হবে।

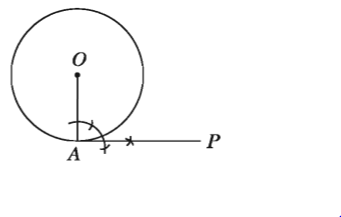
মনে করি, O কেন্দ্রবিশিষ্ট বৃত্তে A একটি বিন্দু। A বিন্দুতে বৃত্তটিতে একটি স্পর্শক আঁকতে হবে।

অঙ্কন:

O, A যোগ করি। A বিন্দুতে OA এর উপর AP লম্ব আঁকি। তাহলে AP নির্ণেয় স্পর্শক।

 

 

প্রমাণ:

OA রেখাংশ A বিন্দুগামী ব্যাসার্ধ এবং AP তার ওপর লম্ব। সুতরাং, AP রেখাই নির্ণেয় স্পর্শক।

বিশেষ দ্রষ্টব্য:

বৃত্তের কোনো বিন্দুতে একটিমাত্র স্পর্শক আঁকা যায়।

সম্পাদ্য ৮.

বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে বৃত্তটির স্পর্শক আঁকতে হবে।

মনে করি, O কেন্দ্রবিশিষ্ট বৃত্তের P একটি বহিঃস্থ বিন্দু। P বিন্দু থেকে ঐ বৃত্তে স্পর্শক আঁকতে হবে।

অঙ্কন:

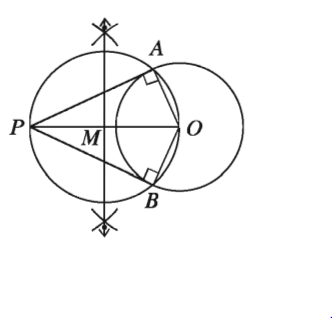
১. PO যোগ করি। PO রেখাংশের মধ্যবিন্দু M নির্ণয় করি।

২. এখন M কে কেন্দ্র করে MO এর সমান ব্যাসার্ধ নিয়ে P একটি বৃত্ত আঁকি। মনে করি, নতুন অঙ্কিত বৃত্তটি প্রদত্ত বৃত্তকে A ও B বিন্দুতে ছেদ করে।

৩. A, P এবং B, P যোগ করি। তাহলে, AP, BP উভয়েই নির্ণেয় স্পর্শক।

 

 

প্রমাণ:

A, O ও B, O যোগ করি। APB বৃত্তে PO ব্যাস।

PAO = এক সমকোণ [::: অর্ধবৃত্তস্থ কোণ সমকোণ]

সুতরাং, OA রেখাংশ AP রেখাংশের ওপর লম্ব। অতএব, O কেন্দ্রিক বৃত্তের A বিন্দুতে AP রেখাংশ একটি স্পর্শক। অনুরূপভাবে, BP রেখাংশও একটি স্পর্শক।

বিশেষ দ্রষ্টব্য:

বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে ঐ বৃত্তে দুইটি ও কেবল দুইটি স্পর্শক আঁকা যায়।

সম্পাদ্য ৯.

কোনো নির্দিষ্ট ত্রিভুজের পরিবৃত্ত আঁকতে হবে।

মনে করি, ABC একটি ত্রিভুজ। এর পরিবৃত্ত আঁকতে হবে। অর্থাৎ, এমন একটি বৃত্ত আঁকতে হবে, যা ত্রিভুজের তিনটি শীর্ষবিন্দু A, B ও C বিন্দু দিয়ে যায়।

অঙ্কন:

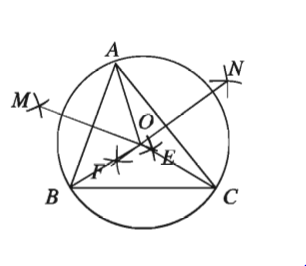
১. AB ও AC রেখাংশের লম্ব সমদ্বিখণ্ডক যথাক্রমে EM ও FN রেখাংশ আঁকি । মনে করি, তারা পরস্পরকে O বিন্দুতে ছেদ করে।

২. A, O যোগ করি। O কে কেন্দ্র করে OA এর সমান ব্যাসার্ধ নিয়ে একটি বৃত্ত আঁকি। তাহলে, বৃত্তটি A, B ও C বিন্দুগামী হবে এবং এই বৃত্তটিই ∆ABC এর নির্ণেয় পরিবৃত্ত।

 

 

প্রমাণ:

B, O ও C, O যোগ করি। O বিন্দুটি AB এর লম্বদ্বিখণ্ডক EM এর ওপর অবস্থিত।

.:. OA = OB, একইভাবে, OA = OC

:. OA = OB = OC

সুতরাং O কে কেন্দ্র করে OA এর সমান ব্যাসার্ধ নিয়ে অঙ্কিত বৃত্তটি A, B ও C বিন্দু তিনটি দিয়ে যাবে। সুতরাং এই বৃত্তটিই ∆ABC এর পরিবৃত্ত।

লক্ষণীয় যে, সূক্ষ্মকোণী ত্রিভুজের ক্ষেত্রে পরিকেন্দ্র ত্রিভুজের অভ্যন্তরে, স্থূলকোণী ত্রিভুজের ক্ষেত্রে পরিকেন্দ্র ত্রিভুজের বহির্ভাগে এবং সমকোণী ত্রিভুজের ক্ষেত্রে পরিকেন্দ্র অতিভুজের ওপর অবস্থিত।

সম্পাদ্য ১০.

কোনো নির্দিষ্ট ত্রিভুজের অন্তবৃত্ত আঁকতে হবে।

মনে করি, ∆ABC একটি ত্রিভুজ। এর অন্তবৃত্ত আঁকতে হবে। অর্থাৎ, ∆ABC এর ভিতরে এমন একটি বৃত্ত আঁকতে হবে, যা BC,CA ও AB বাহু তিনটির প্রত্যেকটিকে স্পর্শ করে।

অঙ্কন :

∠ABC ও ∠ACB এর সমদ্বিখণ্ডক যথাক্রমে BL ও CM আঁকি । মনে করি, তারা O বিন্দুতে ছেদ করে। O থেকে BC M এর ওপর OD লম্ব আঁকি এবং মনে করি, তা BC কে D বিন্দুতে ছেদ করে। O কে কেন্দ্র করে OD এর সমান ব্যাসার্ধ নিয়ে একটি বৃত্ত আঁকি। তাহলে, এই বৃত্তটিই নির্ণেয় অন্তবৃত্ত।

 

 

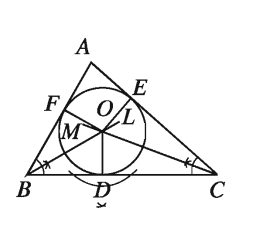
প্রমাণ:

O থেকে AC ও AB এর ওপর যথাক্রমে OE ও OF লম্ব টানি। মনে করি, লম্বদ্বয় বাহুদ্বয়কে যথাক্রমে E ও F বিন্দুতে ছেদ করে।

O বিন্দু ∠ABC এর দ্বিখণ্ডকের ওপর অবস্থিত।

OF = OD

অনুরূপভাবে, O বিন্দু ∠ACB এর দ্বিখণ্ডকের ওপর অবস্থিত বলে OE = OD

OD = OE = OF

সুতরাং O কে কেন্দ্র করে OD এর সমান ব্যাসার্ধ নিয়ে বৃত্ত আঁকলে তা D, E ও F বিন্দু দিয়ে যাবে।

আবার, OD, OE ও OF এর প্রান্তবিন্দুতে যথাক্রমে BC, AC ও AB লম্ব।

সুতরাং বৃত্তটি ∆ABC এর ভিতরে থেকে এর বাহু তিনটিকে যথাক্রমে D, E ও F বিন্দুতে স্পর্শ করে।

অতএব, DEF বৃত্তটিই ∆ABC এর অন্তবৃত্ত হবে।

সম্পাদ্য ১১.

কোনো নির্দিষ্ট ত্রিভুজের বহির্বৃত্ত আঁকতে হবে।

মনে করি, ABC একটি ত্রিভুজ। এর বহির্বৃত্ত আঁকতে হবে। অর্থাৎ, এমন একটি বৃত্ত আঁকতে হবে, যা ত্রিভুজের একটি বাহুকে এবং অপর দুই বাহুর বর্ধিতাংশকে স্পর্শ করে।

অঙ্কন :

AB ও AC বাহুদ্বয়কে যথাক্রম D ও F পর্যন্ত বর্ধিত করি। ∠DBC ও ∠FCB এর সমদ্বিখণ্ডক BM ও CN আঁকি। মনে করি, E এদের ছেদবিন্দু। E থেকে BC এর ওপর EH লম্ব আঁকি এবং মনে করি তা BC কে H বিন্দুতে ছেদ করে। E কে কেন্দ্র করে EH এর সমান ব্যাসার্ধ নিয়ে একটি বৃত্ত আঁকি। তাহলে, এই বৃত্তটিই নির্ণেয় বহির্বৃত্ত।

 

 

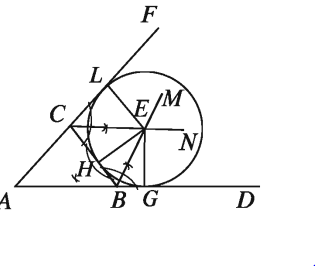
প্রমাণ:

E থেকে BD ও CF রেখাংশের ওপর যথাক্রমে EG ও EL লম্ব টানি। মনে করি, লম্বদ্বয় BD ও CF রেখাংশদ্বয়কে যথাক্রমে G ও L বিন্দুতে ছেদ করে।

E বিন্দুটি ∠DBC এর দ্বিখন্ডকের ওপর অবস্থিত

EH = EG

অনুরূপভাবে, E বিন্দুটি ∠FCB এর দ্বিখণ্ডকের ওপর অবস্থিত বলে EH = EL

:. EH = EG = EL

সুতরাং E কে কেন্দ্র করে EL এর সমান ব্যাসার্ধ নিয়ে অঙ্কিত বৃত্ত H, G এবং L বিন্দু নিয়ে যাবে।

আবার, EH, EG ও EL এর প্রান্তবিন্দুতে যথাক্রমে BC, BD ও CF রেখাংশ তিনটি লম্ব।

সুতরাং বৃত্তটি রেখাংশ তিনটিকে যথাক্রমে H, G ও L বিন্দু তিনটিতে স্পর্শ করে।

অতএব, HGL বৃত্তটিই ∆ABCএর বহিবৃত্ত হবে।

মন্তব্য:

কোনো ত্রিভুজের তিনটি বহির্বৃত্ত আঁকা যায়।