আজকে আমাদের আলোচনার বিষয়ঃ বেলন বা সিলিন্ডার। এটি অষ্টম শ্রেনী গণিতের বৃত্তের অন্তর্গত।

বেলন বা সিলিন্ডার (cylinder)
বেলন বা সিলিন্ডার একটি ত্রিমাত্রিক বক্রাকার ঘনবস্তু যার ভূমি তল দুইটি পরস্পর সমান্তরাল সর্বসম বৃত্ত।
যে ঘনবস্তুর ভূমি তল দুইটি পরস্পর সমান্তরাল ও সর্বসম দুইটি বৃত্ত এবং যার আবদ্ধ বক্রতল বিশিষ্ট গাত্র (body) এমন সকল বিন্দু দিয়ে গঠিত যে সকল বিন্দু একটি নির্দিষ্ট রেখাংশ থেকে সমদূরবর্তী।
একটি আয়তাকার (চিত্র-১) বা বর্গাকার ক্ষেত্রকে তার যেকোনো এক বাহুকে স্থির রেখে ক্ষেত্রটিকে সম্পূর্ণ একবার ঘোরানো হলে একটি ঘনবস্তু (চিত্র-২) উৎপন্ন হয়। এরূপ ঘনবস্তুকে বলা হয় সমবৃত্তভূমিক বেলন বা সমবৃত্তভূমিক সিলিন্ডার (Right circular cylinder) স্থির রেখাটিকে বেলনটির অক্ষ ও এর বিপরীত বাহুকে বেলনটির সৃজক রেখা বলা হয়। এটি বেলনটির উচ্চতা। অপর বাহুটির দৈর্ঘ্য হচ্ছে বেলনটির ব্যাসার্ধ ।
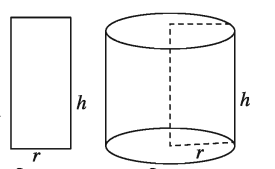
বেলনের পৃষ্ঠের ক্ষেত্রফল নির্ণয় :
মনে করি, একটি সমবৃত্তভূমিক বেলনের ব্যাসার্ধ r এবং উচ্চতা h । বেলনটিকে (যেমন, টিনের একটি ফাঁপা কোঁটা) তার প্রান্ততলদ্বয়ের সাথে লম্ব বরাবর কেটে সমতল আকারের করা হলে হবে একটি আয়তক্ষেত্র, যার প্রান্তদ্বয় হিসেবে যে দুই বাহু পাওয়া যাবে তাদের প্রত্যেকটির দৈর্ঘ্য হবে 2īr (বৃত্তের পরিধি) এবং অপর বাহু হবে বেলনটির উচ্চতা ।
অতএব, সমবৃত্তভূমিকে বেলনটির সমগ্র পৃষ্ঠের বা তলের
ক্ষেত্রফল = প্রাপ্ত তলদ্বয়ের ক্ষেত্রফল + বক্রতলের (যা একটি আয়তক্ষেত্র) ক্ষেত্রফল
= 2 x πr² + 2πr x h
= 2 πr² + 2πrh
= 2 ar (r + h) বর্গ একক

উদাহরণ ৫।
একটি সমবৃত্তভূমিক বেলনের ব্যাসার্ধ 4.5 সে.মি. ও উচ্চতা 6 সে.মি. । বেলনটির বক্রপৃষ্ঠের ক্ষেত্রফল নির্ণয় কর ( π = 3.14)।
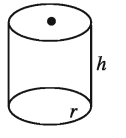
সমাধান :
প্রদত্ত সমবৃত্তভূমিক বেলনটির ব্যাসার্ধ r = 4.5 সে.মি. ও উচ্চতা h = 6 সে.মি. ।
বেলনটির বক্রপৃষ্ঠের ক্ষেত্রফল
= 2rrh = 2 x 3.14 x 4.5 x 6 বর্গ সে.মি.
= 6.28 x 27 বর্গ সে.মি
= 169.56 বর্গ সে.মি
