আজকে আমাদের আলোচনার বিষয়ঃ ভাগশেষ উপপাদ্য। এটি নবম – দশম শ্রেনী গণিতের বীজগাণিতিক রাশি এর অন্তর্গত।

ভাগশেষ উপপাদ্য
নিচের উদাহরণটিতে 6×2 – 7x + 5 কে x – 1 দ্বারা ভাগ করলে ভাগফল ও ভাগশেষ কত?
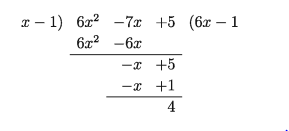
এখানে, ভাজক x – 1, ভাজ্য 6×2 – 7x + 5, ভাগফল 6x – 1 এবং ভাগশেষ 4।
আমরা জানি, ভাজ্য = ভাজক × ভাগফল + ভাগশেষ
এখন যদি আমরা ভাজ্যকে f(x), ভাগফলকে h(x), ভাগশেষকে r ও ভাজককে (x – a) দ্বারা সূচিত করি, তাহলে উপরের সূত্র থেকে পাই,
f(x) = (x – a) . h(x) + r, এই সূত্রটি a এর সকল মানের জন্য সত্য।
উভয়পক্ষে x = a বসিয়ে পাই,
f (a) = (a – a) h (a) + r = 0.h(a) + r = r
সুতরাং, r = f(a)
অতএব, f(x) কে ( x – a) দ্বারা ভাগ করলে ভাগশেষ হয় f(a)। এই সূত্র ভাগশেষ উপপাদ্য (Remainder theorem) নামে পরিচিত। অর্থাৎ, ধনাত্মক মাত্রার কোনো বহুপদী f(x) কে (x – a) আকারের বহুপদী দ্বারা ভাগ করলে ভাগশেষ কত হবে তা ভাগ না করে বের করার সূত্রই হলো ভাগশেষ উপপাদ্য।
উপরের উদাহরণে a = 1 হলে f(x) = 6×2 – 7x + 51
f(1) = 6-7 + 5 4 যা ভাগশেষের সমান। ভাজক বহুপদী (x – a) এর মাত্রা 1, ভাজক = যদি ভাজ্যের উৎপাদক হয়, তাহলে ভাগশেষ হবে শূন্য। আর যদি উৎপাদক না হয়, তাহলে ভাগশেষ থাকবে এবং তা হবে অশূন্য কোনো সংখ্যা। তবে সাধারণভাবে বলতে গেলে ভাগফল ভাজকের থেকে কম মাত্রার একটি বহুপদী হবে।

অনুসিদ্ধান্ত ১১.
(x – a), f(x) এর উৎপাদক হবে, যদি এবং কেবল যদি f(a) = 0 হয়।
প্রমাণ:
ধরি, f(a) = 0। অতএব, ভাগশেষ উপপাদ্য অনুযায়ী, f(x) কে (x – a) দ্বারা ভাগ করলে ভাগশেষ শূন্য হবে। অর্থাৎ, (x – a), f(x) এর একটি উৎপাদক হবে।
বিপরীতক্রমে, ধরি, (x – a), f(x) এর একটি উৎপাদক।
অতএব, f(x) = (x – a) . h (x), যেখানে h (x) বহুপদী।
উভয়পক্ষে x = a বসিয়ে পাই,
f(a) = (a – a) . h(a) = 0
f (a) = 0
সুতরাং, কোনো বহুপদী f(x), (x – a) দ্বারা বিভাজ্য হবে যদি এবং কেবল যদি f(a) = 0 হয়। এই সূত্র উৎপাদক উপপাদ্য (Factor theorem) নামে পরিচিত।
প্রতিজ্ঞা ১২.
যদি f(x) এর মাত্রা ধনাত্মক হয় এবং a ≠ 0 হয়, তবে f(x) কে (ax + b) দ্বারা ভাগ করলে ভাগশেষ হয় f(-b/a).
প্রমাণ:
ভাজক ax + b (a ≠ 0) এর মাত্রা 1।
সুতরাং আমরা লিখতে পারি,f(x) = ( ax + b ) · h(x) + r = a (x + b/a ) · h(x) + r
f(x) = (x + b/a) · a · h(x) + r
দেখা যাচ্ছে যে, f(x) কে (x + b/a) দ্বারা ভাগ করলে ভাগফল হয়, a. h (x) এবং ভাগশেষ হয় r।
এখানে, ভাজক = x – (-b/a)
সুতরাং ভাগশেষ উপপাদ্য অনুযায়ী, r = f (-b/a)
অতএব, f(x) কে (ax + b) দ্বারা ভাগ করলে ভাগশেষ হয় (-b/a)
অনুসিদ্ধান্ত ১৩.
ax + b, a ≠ 0 হলে, রাশিটি কোনো বহুপদী f(x) এর উৎপাদক হবে, যদি এবং কেবল যদি (-b/a) = 0 হয়।
প্রমাণ:
a ≠ 0, ax+b = (x + b/a), f(x) এর উৎপাদক হবে, যদি এবং কেবল যদি ।
= x -(-b/a), f(x) এর একটি উৎপাদক হয়। অর্থাৎ, যদি এবং কেবল যদি f (-b/a) = 0 হয়। ভাগশেষ উপপাদ্যের সাহায্যে উৎপাদক নির্ণয়ের এই পদ্ধতিকে শূন্যায়ন পদ্ধতি (Vanishing method) বলে।

উদাহরণ ৩০.
23 − x – 6 কে উৎপাদকে বিশ্লেষণ কর ।
সমাধান:
এখানে, f(x) = x – 6 একটি বহুপদী। এর ধ্রুবপদ – 6 এর উৎপাদকগুলো হচ্ছে = ±1, ±2, ±3, ±6
এখন, x = 1, −1 বসিয়ে দেখি, f(x) এর মান শূন্য হয় না।
কিন্তু x = 2 বসিয়ে দেখি, f(x) এর মান শূন্য হয়।
অর্থাৎ, f(2) = 23 – 2 – 6 = 8 – 2 – 6 = 0
সুতরাং, x – 2, f(x) বহুপদীটির একটি উৎপাদক।
f(x) = x3 – x – 6
= x3 – 2×2 + 2×2 – 4x + 3x – 6
= x2 (x – 2) + 2x(x – 2 ) + 3 (x – 2 )
= (x − 2)(x² + 2x+3)
উদাহরণ ৩১.
x3 – 3ay2 + 2y3 এবং x2 + xy – 2y2 কে উৎপাদকে বিশ্লেষণ কর।
সমাধান:
এখানে, কে চলক এবং y কে ধ্রুবক হিসেবে বিবেচনা করি।
প্রদত্ত রাশিকে x-এর বহুপদী বিবেচনা করে
ধরি, f(x) = x – 3xy + 2y3
তাহলে, f (y) = y3 – 3y . y2 + 2y3 = 3y3 – 3y = 0
.:. (x – y), f(x) এর একটি উৎপাদক।
এখন, x³ – 3xy² + 2y³
= x³- x²y + x²y-xy2-2xy²+2y³
= x² (x − y) + xy(x − y) − 2y² (x − y) = (x − y)(x² + xy – 2y2)
আবার ধরি, g(x) = x2 + xy – 2y 2
g(y) = y²+ y² – 2y2=0
(x – y), g ( 2 ) এর একটি উৎপাদক
g(x) = x² + xy-2y2
= x²- xy + 2xy – 2y2
= x(x − y) +2y(x − y)
= (x − y)(x+2y)
..x³-3x²+2y³ = (x-y)2(x+2y)

উদাহরণ ৩২.
54×4 + 27x3a – 16x – 8a কে উৎপাদকে বিশ্লেষণ কর। –
সমাধান:
ধরি, f(x) = 54×4 + 27aa – 16a – 8a
তাহলে, f (-1/2 a) = 54 (-1/2 a)4 +27a(-1/2 a)3 – 16(-1/2 a) – 8a
= (27/8) a4 – (27/8) a4+8a-8a = 0
x – (-1/2 a) = x + a/2 = 1/2(2x + a), f(x) এর একটি উৎপাদক
অর্থাৎ, (2x + a), f(x) এর একটি উৎপাদক।
এখন, 54×4 + 27x³a – 16x – 8a
= 27x³ (2x+a) -8(2x+a)
= (2x+a) (27×3—8)
= (2x+a){(3x)³ – (2)3}
= (2x + a) (x – 2 ) (9×2 + 6x + 4 )

উদাহরণ ৩৩.
g(a) = a3 + a2 + 10 – 8, f (a) = a3 – 9 + (a + 1)3।
ক) g (a) কে ( a – 2 ) দ্বারা ভাগ করলে ভাগশেষ কত হবে তা নির্ণয় কর।
খ) f(a) কে উৎপাদকে বিশ্লেষণ কর।
সমাধান:
ক) দেওয়া আছে, g (a) = a3 + a2 + 10a
ভাগশেষ উপপাদ্য অনুসারে g (a) কে ( a – 2 ) দ্বারা ভাগ করলে ভাগশেষ হবে g(2)।
g(2) = 23 +22+10-2-88+4+20-832-8=24
g (2) = 24
নির্ণেয় ভাগশেষ 24
খ) f(a) = a³-9+ (a + 1)3
f(a) একটি বহুপদী, a = 1 বসালে বহুপদীটির মান শূন্য হয়।
ফলে (a – 1) বহুপদীটির একটি উৎপাদক।
f(a) = a³-9+a³+3a²+3a+1=2a3+3a² + 3a – 8
=2a3 – 2a2 + 5a2 – 5a+8a-8
=2a2(a – 1)+5a(a – 1)+8(a – 1)
= (a− 1)(2a² + 5a +8)
a³ −9+ (a + 1)3 = (a− 1)(2a² + 5a +8)
অনুশীলনী
উৎপাদকে বিশ্লেষণ কর :
১. 3a3+2a +5.
২. x3-7xy2-6y3
৩. x3+2×2-5x-6
৪. x3+4x²+x-6
৫. a3+3a +36
৬. a4- 4a+3
৭. a3-a²-10a-8
৮. x³-3x²+4x-4
৯. a3-7a2b+7ab2-b3
১o. x³-x-24
১১. x3+6x²+11x+6
১২. 2×4-3×3-3x-2
১৩. 4×4 +12×3+7×2-3x-2
১৪. x6-x5+x4-x3+x2-x
১৫. 4×3-5×2+5x-1
১৬. 18×3+15×2-x-2
