ভাগশেষ ও উৎপাদক উপপাদ্য

আজকে আমরা আলোচনা করবো  ভাগশেষ ও উৎপাদক উপপাদ্য সম্পর্কে । যা উচ্চতর গণিতের বীজগানিতিক রাশি অংশের অন্তর্গত।

 

 

ভাগশেষ ও উৎপাদক উপপাদ্য

এই অনুচ্ছেদে শুধু x চলকের বহুপদী বিবেচনা করা হবে। প্রথমে দুইটি উদাহরণ বিবেচনা করি।

উদাহরণ ৪.

যদি P(x) = x2 – 5x + 6 হয়, তবে P(x) কে (x – 4) দ্বারা ভাগ কর এবং দেখাও যে, ভাগশেষ P(4) এর সমান।

সমাধান:

P(x) কে (x – 4 ) দ্বারা নিচের মতো ভাগ করি।

 

 

এখানে ভাগশেষ 2 ।

যেহেতু P(4) = 42 – 5 ( 4 ) + 6 = 2, সুতরাং, ভাগশেষ P(4) এর সমান।

উদাহরণ ৫.

যদি P(x) = ax3 + b + c হয়, তবে P(x) কে x – m দ্বারা ভাগ করে দেখাও যে, ভাগশেষ P(m) এর সমান।

সমাধান:

P(x) কে m দ্বারা নিচের মতো ভাগ করি।

 

 

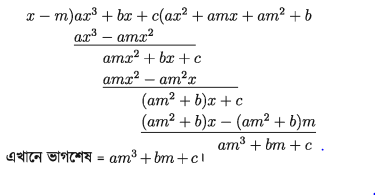
আবার, P (m) = am³ + bm + c, সুতরাং ভাগশেষ P (m) এর সমান।

উপরের এই উদাহরণ দুইটি থেকে নিম্নের প্রতিজ্ঞাটি সম্পর্কে ধারণা পাওয়া যায়।

প্রতিজ্ঞা ১

(ভাগশেষ উপপাদ্য) যদি P(x) ধনাত্মক মাত্রার বহুপদী হয় এবং a কোনো নির্দিষ্ট সংখ্যা হয়, তবে P(x) কে x – a দ্বারা ভাগ করলে ভাগশেষ P(a) হবে।

প্রমাণ:

P(x) কে x – a দ্বারা ভাগ করলে ভাগশেষ হয় 0 অথবা অশূন্য ধ্রুবক হবে।

মনে করি, ভাগশেষ R এবং ভাগফল Q(x); তাহলে, ভাগের নিয়মে, সকল x এর জন্য

P(x) = (x − a)Q(x) + R

যাতে x = a বসিয়ে পাই, P(a) = 0. Q (a) + R = R

সুতরাং, P(x) কে x – a দ্বারা ভাগ করলে ভাগশেষ P(a) হবে।

 

 

উদাহরণ ৬.

P(x) = x3 – 8x 2 + 6x + 60 কে x + 2 দ্বারা ভাগ করলে, ভাগশেষ কত হবে?

সমাধান:

যেহেতু x + 2 = x – (-2) = (x – a) যেখানে a =  -2,

সুতরাং, ভাগশেষ = P(-2) = (-2) 3 – 8 (2) 2 + 6 ( 2 ) + 60 = 81

প্রতিজ্ঞা ১ এর অনুকরণে নিচের প্রতিজ্ঞাটিও প্রমাণ করা যায়।

প্রতিজ্ঞা ২.

যদি P(x) ধনাত্মক মাত্রার বহুপদী হয় এবং a ≠ 0 হয়, তবে P(x) কে ax + b দ্বারা ভাগ করলে ভাগশেষ P হবে।

উদাহরণ ৭.

বহুপদী P(x) = 36×2 – 8x + 5 কে (2x – 1) দ্বারা ভাগ করলে ভাগশেষ কত হবে?

সমাধান:

নির্ণেয় ভাগশেষ P (2) = 2 ³ (1) * – 8 ( 1 ) · 36 +59-4+5=10

 

 

উদাহরণ ৮.

যদি P(x) = 5×3 + 6×2 – ax + 6 কে তবে a এর মান নির্ণয় কর। -2 দ্বারা ভাগ করলে ভাগশেষ 6 হয়,

সমাধান:

P(x) কে 2 দ্বারা ভাগ করলে ভাগশেষ হবে,

P(2) = 5(2)³ +6(2)2 — a(2) + 6 = 40 + 24-2a+6=70-2a

শর্তানুসারে, 70 – 2a = 6 বা, 2a = 70 – 6 = 64 অর্থাৎ a = = 32

উদাহরণ ৯.

যদি P(x) = x3 + 5×2 + 6x + 8 হয় এবং P(x) কে x – a এবং x – b দ্বারা ভাগ করলে একই ভাগশেষ থাকে যেখানে a ≠ b, তবে দেখাও যে, a2 + b2 + ab + 5a + 5b + 6 = 0

সমাধান:

P(x) কে x – a দ্বারা ভাগ করলে ভাগশেষ হবে P(a) = a3 + 5a2 + 6a + 8,

এবং P(x) কে x – b দ্বারা ভাগ করলে ভাগশেষ হবে P(b) = b3 + 5b2 + 6b + 8

শর্তানুসারে, a3 + 5a2 + 6a +8 = b3 + 5b2 + 6b +8
বা, a3 – b3 + 5 (a2 – b2 ) + 6 (a – b) = 0
বা, (a – b) (a2 + b2 + ab + 5a + 5b + 6) = 0
. a2 + b2 + ab + 5a + 5b + 6 = 0, যেহেতু a + b

প্রতিজ্ঞা ৩(উৎপাদক উপপাদ্য)

যদি P(x) ধনাত্মক মাত্রার বহুপদী হয় এবং P(a) = 0 হয়, তবে P(x) এর একটি উৎপাদক x – a হবে।

প্রমাণ:

P(x) বহুপদীকে x – a দ্বারা ভাগ করলে ভাগশেষ উপপাদ্য অনুযায়ী ভাগশেষ = P(a), যা প্রদত্ত শর্ত অনুযায়ী 0। অর্থাৎ P(x) বহুপদী x – a দ্বারা বিভাজ্য।

x – a হচ্ছে P(x) এর একটি উৎপাদক ।

আরও দেখুনঃ

• বাস্তব সমস্যা সমাধানে সেট