আজকে আমরা আলোচনা করবো ভেক্টরের বিয়োগ । যা উচ্চতর গণিতের সমতলীয় ভেক্টর অংশের অন্তর্গত।

ভেক্টরের বিয়োগ
u এবং v ভেক্টরদ্বয়ের বিয়োগফল u – v বলতে u এবং -v (অর্থাৎ v এর বিপরীত ভেক্টর) ভেক্টরদ্বয়ের যোগফল u + (−v) বুঝায়।

ভেক্টর বিয়োগের ত্রিভুজ বিধি:
u এবং v এর আদিবিন্দু একই হলে u – v সেই ভেক্টর, যার আদিবিন্দু হচ্ছে v এর অন্তবিন্দু এবং যার অন্তবিন্দু হচ্ছে u এর অন্তবিন্দু। সংক্ষেপে একই আদিবিন্দু বিশিষ্ট দুইটি ভেক্টরের বিয়োগফল হচ্ছে অন্তবিন্দুদ্বয় দ্বারা বিপরীতক্রমে গঠিত ভেক্টর।
সুতরাং u = AB , v = AC হলে u – v = CB, অর্থাৎ, AB – AC = CB । নিচে আমরা এটা প্রমাণ করবো।
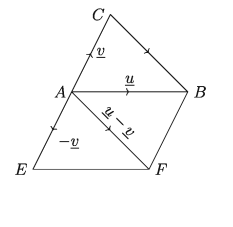
প্রমাণ:
CA রেখাংশকে এমনভাবে বর্ধিত করি যেন AE = CA হয়। AEFB সামান্তরিক গঠন করি। ভেক্টর যোগের সামান্তরিক বিধি অনুযায়ী, AB + AB = AF
আবার AFBC একটি সামান্তরিক, কেননা BF = AE = CA এবং BF || AE বলে BF || CA
.:. AF = CB (ভেক্টর স্থানান্তর), কিন্তু AE = -v এবং AB = u
সুতরাং u – v = CB প্রমাণিত হলো।

শূন্য ভেক্টর
যে ভেক্টরের মান শূন্য এবং যার দিক নির্ণয় করা যায় না তাকে শূন্য ভেক্টর বলে ।
u যেকোনো ভেক্টর হলে u + (- u) কি হবে?
ধরি, u = AB তখন –u = BA,
ফলে u – u = AB + BA = AA [ত্রিভুজ বিধি অনুযায়ী]
কিন্তু AA কি ধরনের ভেক্টর? এটি একটি বিন্দু ভেক্টর, অর্থাৎ এর আদিবিন্দু ও অন্তবিন্দু একই বিন্দু; সুতরাং দৈর্ঘ্য শূন্য। অর্থাৎ AA দ্বারা A বিন্দুকেই বুঝতে হবে। দৈর্ঘ্য শূন্য এরূপ ভেক্টরকে শূন্য ভেক্টর বলা হয় এবং 0 দ্বারা সূচিত করা হয়। এটি একমাত্র ভেক্টর যার কোনো নির্দিষ্ট দিক বা ধারক রেখা নেই ।
শূন্য ভেক্টরের অবতারণার ফলে আমরা বলতে পারি যে, u + (-u) = 0 এবং u + 0 = 0 + u = u বস্তুত শূন্য ভেক্টরের সঙ্গে শেষোক্ত অভেদ নিহিত রয়েছে।
