ভেক্টরের যোগ

আজকের আলোচনার বিষয়ঃ ভেক্টরের যোগ। যা উচ্চতর গণিতের  সমতলীয় ভেক্টর অংশের অন্তর্গত।

 

 

ভেক্টরের যোগ

কোনো u ভেক্টরের প্রান্তবিন্দু থেকে অপর একটি ভেক্টর v আঁকা হলে u+ v দ্বারা এরূপ ভেক্টর বুঝায় যার আদিবিন্দু u এর আদিবিন্দু এবং যার প্রান্তবিন্দু v এর প্রান্তবিন্দু। মনে করি AB = u , BC = v এরূপ দুইটি ভেক্টর যে, u এর প্রান্তবিন্দু v এর আদিবিন্দু। তাহলে u এর আদিবিন্দু এবং v এর প্রান্তবিন্দু সংযোজক AC ভেক্টরকে u ও v ভেক্টরদ্বয়ের সমষ্টি বলা হয় এবং u+v দ্বারা সূচিত হয়।

 

 

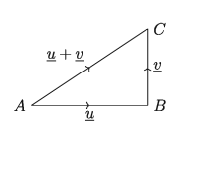
ভেক্টর যোগের ত্রিভুজ বিধি:

উপরের চিত্রে u ও v সমান্তরাল না হলে u, v এবং u + v ভেক্টরত্রয় দ্বারা ত্রিভুজ উৎপন্ন হয় বলে উপরোক্ত যোজন পদ্ধতিকে ত্রিভুজ বিধি বলা হয়।

ভেক্টর যোগের ত্রিভুজ বি-ধির অনুসিদ্ধান্ত হিসেবে ভেক্টর যোগের সামান্তরিক বিধি নিম্নরূপ:

ভেক্টর যোগের সামান্তরিক বিধি :

কোনো সামান্তরিকের দুইটি সন্নিহিত বাহু দ্বারা দুইটি ভেক্টর u ও v এর মান ও দিক সূচিত হলে, ঐ সামান্তরিকের যে কর্ণ u ও v ভেক্টরদ্বয়ের ধারক রেখার ছেদবিন্দুগামী তা দ্বারা u + v ভেক্টরের মান ও দিক সূচিত হয়। নিচে আমরা এটার প্রমাণ দেখবো।

 

 

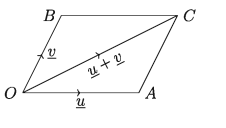
প্রমাণ:

মনে করি, যেকোনো বিন্দু থেকে অঙ্কিত u এবং v ভেক্টরদ্বয় OA এবং OB দ্বারা সূচিত হয়েছে। OACB সামান্তরিক ও তার OC কর্ণ অঙ্কন করি। তাহলে ঐ সামান্তরিকের OC কর্ণ দ্বারা u এবং v এর যোগফল সূচিত হবে। অর্থাৎ OC = u + v।

OACB সামান্তরিকের OB ও AC সমান ও সমান্তরাল।

:. AC = OB = v [ভেক্টর স্থানান্তর]

ত্রিভুজ বিধি কাজে লাগিয়ে u + v = OÀ + OB = 0À + AC = OC  [প্রমাণিত]

 

দ্রষ্টব্য :

ক) দুই বা ততোধিক ভেক্টরের যোগফলকে তাদের লব্ধিও বলা হয়। বল বা বেগের লব্ধি নির্ণয়ের ক্ষেত্রে ভেক্টর যোগের পদ্ধতি অনুসরণ করতে হয়।

খ) দুইটি ভেক্টর সমান্তরাল হলে তাদের যোগের ক্ষেত্রে সামান্তরিক বিধি প্রযোজ্য নয়, কিন্তু ত্রিভুজ বিধি সকল ক্ষেত্রে প্রযোজ্য।

 

ভেক্টরের যোগের নিয়ম নিয়ে বিস্তারিত ঃ